1.1 " 三维 "-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节三维

  折叠 展开

  三维

  播放段落

  You live in a three-dimensional world. Solid objects, such as yourself, are three dimensional . In order to better understand why your world is three dimensional, consider zero, one, and two dimensions .
  ::你生活在一个三维的世界中。像你自己这样的固态物体是三维的。为了更好地了解为什么你的世界是三维的, 考虑零,一和两个维。

  播放段落

  Zero Dimensions
  ::零维度

  播放段落

  In math, a point is zero dimensional. It has no length or width.
  ::在数学中,一个点是零维。它没有长度或宽度。

  ---

  播放段落

  One Dimension
  ::一个层面

  播放段落

  A line segment has one dimension. It has a length .
  ::线段有一个维度。它有一个长度。

  播放段落

  A number line is an example of a line , which is like an infinitely long line segment with no endpoints. Like a line segment, a line is one-dimensional , so y ou only need a single number to describe a point on a number line (in the interactive below, the location of point A is -2). Remember that by definition, a line is straight.
  ::数字线是一个线的示例,它就像一个无端点的无限长的线段。像一条线段一样,一线是一维的,所以只需要一个数字来描述数字线上的点(在下面的互动线中,A点的位置是 -2)。 记住,按照定义,一线是直线。

  ---

  播放段落

  Two Dimensions
  ::两维

  播放段落

  A shape has two dimensions. Each dimension can be compared to a line segment because it has a specific maximum length and width . 
  ::一个形状有两个维度。每个维度都可以与一个线段比较,因为它有特定的最长长度和宽度。

  播放段落

  The rectangular coordinate system that is used for graphing is an example of a plane , which is like an infinitely large shape without measurable sides . To describe a point on the rectangular coordinate system, you need two numbers: the $\begin{array}{r}x\end{array}$ -coordinate and the $\begin{array}{r}y\end{array}$ -coordinate (in the interactive below, the point P is located at (3, -2).
  ::用于图形绘制的矩形坐标系统是平面的一个例子,平面就像一个无限大的形状,没有可测量的侧面。要描述矩形坐标系统上的某个点,您需要两个数字:x坐标和Y坐标(在下文互动部分中,P点位于3,2-2)。

  ---

  播放段落

  Basic Geometric Definitions: How many dimensions?
  ::基本几何定义:有多少维度?

  播放段落

  Use the interactive below to explore how the position of points may describe figures with different numbers of dimensions. Collinear points may describe a line (1 dimension) where non-collinear points may describe a figure such as a triangle (2 dimensions).
  ::用下文的交互作用来探讨点的位置如何描述具有不同尺寸的数字。 相近点可以描述一行(1维),其中非线性点可以描述三角形(2维)等数字。

   

   

  ---

  播放段落

  Three Dimensions
  ::三个层面

  播放段落

  A solid has three dimensions: length, width and height .
  ::固态有三个维度:长度、宽度和高度。

  播放段落

  You can turn the rectangular coordinate system into a three-dimensional coordinate system by creating a third axis, the $\begin{array}{r}z\end{array}$ -axis , that is perpendicular to both the $\begin{array}{r}x\end{array}$ -axis and $\begin{array}{r}y\end{array}$ -axis .
  ::您可以将矩形坐标系统转换成三维坐标系统, 创建一个与 x 轴和 y 轴垂直的第三个轴, 即 z 轴。

  播放段落

  To describe a point on the Cartesian coordinate system in three-dimensional space , you need three numbers, the $\begin{array}{r}x\end{array}$ -coordinate , the $\begin{array}{r}y\end{array}$ -coordinate and the $\begin{array}{r}z\end{array}$ -coordinate . The general form of a coordinate in three dimensions is $\begin{array}{r}(x,y,z).\end{array}$
  ::要描述三维空间的笛卡尔坐标系统上的一个点, 您需要三个数字、 x 坐标、 Y 坐标和 z 坐标。 三个维的坐标的一般形式是 (x,y,z) 。

  播放段落

  Because paper and screens have dimensions of two, it is hard to represent three-dimensional objects on them. Artists use perspective techniques to allow the viewer to imagine the three dimensions.
  ::由于纸张和屏幕具有两个维度, 很难在它们上代表三维天体。 艺术家使用视角技术让观众想象三个维度。

   

   

  ---

  播放段落

  The number of values needed to describe a location tells you what dimensional space the location is in .
  ::描述位置所需的值数可以说明位置所在的维度空间。

   

   

  ---

  播放段落

  Determining Number of Dimensions
  ::确定尺寸数量

  播放段落

  You graph a line on a rectangular coordinate system. How many dimensions does that line have?
  ::您在矩形坐标系统中绘制一条线。 该线有多少维度 ?

  播放段落

  Even though the rectangular coordinate system has two dimensions, the line itself has only one dimension.
  ::尽管矩形坐标系统有两个维度,但线本身只有一个维度。

  播放段落

  You plot a point on a line. How many dimensions does the point have?
  ::您在线上绘制一个点。 该点有多少维度 ?

  播放段落

  Even though the line has one dimension, the point is simply a location on the line, and the point itself has zero dimensions.
  ::即使线有一个维度, 点只是线上的一个位置, 点本身是零维度 。

  ---

  播放段落

  Determining Number of Points
  ::确定点数

  播放段落

  How many points make up a line?
  ::有多少点组成一条线?

  播放段落

  A line is made up of points.
  ::一条线由点组成。

  ---

  播放段落

  Geometry Terms: Collinear Constellations
  ::几何术语: 星座星座

  播放段落

  Play with the interactive below to explore and understand Geometric Terms.
  ::与下面的交互式游戏一起探索和理解几何术语。

   

   

  ---

  播放段落

  Describing Objects
  ::描述对象

  播放段落

  Is the edge of a desk best described as a point, a line, a plane, or solid?
  ::桌子的边缘是最好的 描述为点,线,平面,还是固态?

  播放段落

  The edge of a desk is best described as a . It has one dimension.
  ::桌面的边缘最好描述为一个。 它有一个维度。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  How might you imagine a four-dimensional figure?
  ::你怎么能想象一个四维的图象呢?

  播放段落

  The world we experience is three-dimensional, so we can visualize three dimensions with real examples. Four dimensions don't exist in our world, so it is very hard to imagine an object with dimension four. It helps to think about how two dimensions become three dimensions. A shape with dimension two moves up and down to create a solid with dimension three. Similarly, you can imagine a solid (such as a cube) with dimension three, moving within itself to create a tesseract, with dimension four.
  ::我们所经历的世界是三维的, 所以我们可以用真实的例子来想象三个维度。 四个维度在我们的世界中不存在, 因此很难想象一个有四维的物体。 它有助于思考两个维度如何成为三个维度。 一个有二维的形状上下移动, 以创造一个有三维的固态。 同样, 你可以想象一个有三维的固态( 比如一个立方体), 以三维的立方体内部移动, 以创造一个有四维的特塞克。

  

  播放段落

  Example 2
  ::例2

  播放段落
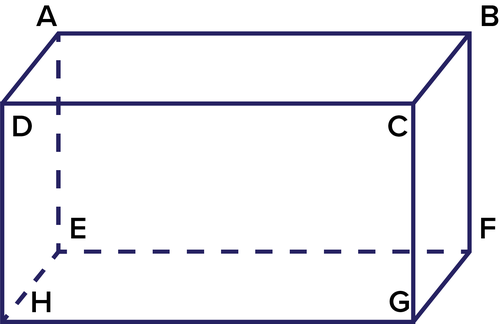
  1. The three-dimensional figure above is defined by 8 points . Identify three of the points in the figure using the letters they are labeled with. How many dimensions do each of those  points have?
     ::上面的三维图由 8 个点定义。 使用它们所标注的字母来标明图中的三个点。 每个点有多少维度 ?

  播放段落

  Any points that make up this prism will work. These points are called vertices . For example, point $\begin{array}{r}A\end{array}$ , point $\begin{array}{r}B\end{array}$ , point $\begin{array}{r}C\end{array}$ . Although the rectangular prism is three-dimensional, each point is simply a location in space, and as such has zero dimensions.
  ::构成此棱晶的任何点都会有效。 这些点被称为顶点。 例如, 点 A, 点 B, 点 C。 虽然矩形棱柱是三维的, 但每个点都是空间中的一个位置, 因而是零维 。

  播放段落
  2. Identify the line segments from the figure above. How many dimensions does each line segment have?
     ::从上图中确定线段。 每个线段有多少维度?

  播放段落

  Any line segments that make up this prism will work. These line segments are called edges. For example, $\begin{array}{r}\overline{AB}\end{array}$ , $\begin{array}{r}\overline{BC}\end{array}$ , $\begin{array}{r}\overline{CD}\end{array}$ . Although the figure is three-dimensional, each edge is only a line segment, and so is one-dimensional.
  ::构成此棱镜的任何线段都会有效。 这些线段被称为边缘。 例如, AB 、 BC 、 CD 。 虽然数字是三维的, 但每个边缘只是一条线段, 而一维也是如此 。

  播放段落
  3. The figure has 6 sides . Identify one of the sides on the prism. How many dimensions does each side have?
     ::数字有6个侧面。在棱镜上找出一个侧面。 每一侧有多少维面?

  播放段落

  Any sides that make up this prism will work. A s part of a three-dimensional figure, they are two-dimensional shapes called faces. For example, $\begin{array}{r}ABCD\end{array}$ (the top face), $\begin{array}{r}BCGF\end{array}$ (the right side), and $\begin{array}{r}CGHD\end{array}$ (the front face).
  ::构成这一棱镜的任何一面都会起作用。 作为三维图的一部分,它们是二维的形状,称为面孔。例如,ABCD(顶面)、BCGF(右面)和CGHD(前面)。

  Summary

  播放段落 A point is a zero dimensional object, having no length or width. ::点是指无长度或宽度的零维对象。 播放段落 A line segment has one dimension: length. ::线段有一个维度:长度。 播放段落 A shape has two dimensions: length and width. ::形状有两个维度:长度和宽度。 播放段落 A solid has three dimensions: length, width and height. ::固态有三个维度:长度、宽度和高度。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. In your own words, explain why a line has one dimension and a plane has two dimensions.
  ::1. 用你自己的话来说,请解释为什么一条线有一个维度,一架飞机有两个维度。

  播放段落

  2. Give a real-world example of something with one dimension.
  ::2. 举一个具有一个层面的现实世界的例子。

  播放段落

  3. Give a real-world example of something with two dimensions.
  ::3. 举一个具有两个层面的现实世界的例子。

  播放段落

  4. Give a real-world example of something with three dimensions.
  ::4. 举一个具有三个层面的现实世界的例子。

  播放段落

  Use the figure below for #5-#6.
  ::使用下图的# 5-# 6。

  

  播放段落

  5. Points are considered coplanar if they lie on the same plane. What's an example of a point that is coplanar with points $\begin{array}{r}H,G\end{array}$ and $\begin{array}{r}E\end{array}$ ?
  ::5. 如果点位于同一平面上,则点被视为共平面。

  播放段落

  6. What's an example of a point that is coplanar with points $\begin{array}{r}A,D\end{array}$ and $\begin{array}{r}E\end{array}$ ?
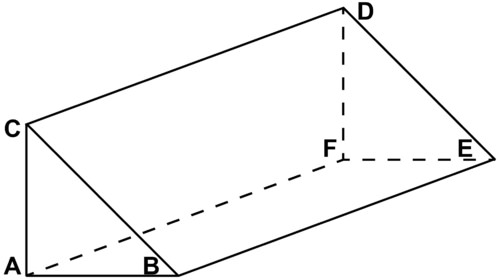
  ::6. 一个点与A、D和E点相交的点的例子是什么?

  播放段落

  Use the figure below for #7-#12.
  ::使用下图的 # 7 - # 12 。

  

  播放段落

  7. Name three points from the figure above.
  ::7. 从上图中列出三点。

  播放段落

  8. Name three line segments from the figure above.
  ::8. 从上图中列出三个行段。

  播放段落

  9. Name three planes from the figure above.
  ::9. 从上图中列出三架飞机。

  播放段落

  10. Name a point that is coplanar with points $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B.\end{array}$
  ::10. 列出一个与A点和B点相交的点。

  播放段落

  11. Name another point that is coplanar with points $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B\end{array}$ , but not also coplanar with your answer to #10 such that all four points are on the same plane.
  ::11. 另列出一个点,即与A点和B点为共平板,但不包括与你对第10点的答复为共平板,因此所有四个点都在同一平面上。

  播放段落

  12. Name a point that is coplanar with $\begin{array}{r}B,C\end{array}$ and $\begin{array}{r}E\end{array}$ .
  ::12. 指出与B、C和E相交的点。

  播放段落

  13. A plane has a dimension of ____.
  ::13. 飞机的尺寸为______。

  播放段落

  14. A line segment has a dimension of ____.
  ::14. 线段具有___的维度。

  播放段落

  15. A cube has a dimension of ____.
  ::15. 立方体的尺寸为____。

  播放段落

  16. If two lines are perpendicular, how many right angles are formed? Why?
  ::16. 如果两条直线是垂直的,则形成多少右角度?为什么?

  播放段落

  17. If two lines in a plane are parallel and a third line in the plane is perpendicular to one of them, what can we conclude? Why?
  ::17. 如果飞机上两条线是平行的,而飞机上第三条线与其中一条线是垂直的,那么我们可以得出什么结论?为什么?

  播放段落

  18. How many lines can be perpendicular to a line through a given point in a plane? Why?
  ::18. 有多少条线能够直通一线,穿过飞机上某一点的一条线?为什么?

  播放段落

  19. Is it possible for two lines in different planes to intersect? Why or why not? Is it appropriate to call these lines parallel? Why or why not?
  ::19. 不同平面的两条线是否可能相互交叉?为什么或为什么没有?将这些线平行起来是否合适?为什么或为什么没有?

  播放段落

  20. Bethany drives north for 2 miles, west for 3 miles, north for 4 miles, then east for 1 mile. Which pairs of segments are perpendicular, which are parallel?
  ::20. Bethany北行2英里,西行3英里,北行4英里,东行1英里。

  播放段落

  21. We can think of space in terms of dimensions. For example, a two-dimensional space is called a plane. A three-dimensional space is, well, a 3-dimensional space! What's a one-dimensional space called? How about a zero-dimensional space? The intersection of two distinct two-dimensional spaces is a space of how many dimensions? The intersection of two distinct one-dimensional spaces is a space of how many dimensions? Explain your answers. Extend this idea to three-dimensions and beyond.
  ::21. 我们可以从维度的角度来思考空间,例如,二维空间称为平面。三维空间是一个三维空间!什么是一维空间?一个零维空间如何?两个截然不同的二维空间的交叉点是一个多维空间的交叉点?两个截然不同的一维空间的交叉点是一个多维空间的交叉点?解释你的答案。把这个想法扩大到三维空间和更多空间。

  播放段落

  22. Give examples of real-world scenarios that can be modeled by objects of different dimensions. Do you think that there are any real-world objects that are two-dimensional? Why or why not? Do you think it is possible to model any real-world scenario with more than three-dimensions? Why or why not?
  ::22. 请举例说明可以由不同维度的物体模拟的真实世界情景。你是否认为任何真实世界的物体是二维的?为什么?为什么或为什么不?你是否认为可以用三个以上维度以上的物体模拟任何真实世界情景?为什么或为什么不能?

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。