1.3多边形 - 定义、类型、属性、互动和实例-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 多边形 - 定义、类型、属性、互动和示例

  Collapse Expand

  多边形 - 定义、类型、属性、互动和示例

  播放段落

  What is a Polygon?
  ::什么是多边形?

  播放段落

  A polygon is a shape bounded by a number of straight lines. A polygon is usually classified by its number of sides and its properties.
  ::多边形是若干条直线所捆绑的形状。多边形通常按其侧面数和属性进行分类。

  播放段落

  Polygon Chart
  ::多边形图图

  播放段落 Sides ::侧面	播放段落 Name of Polygon ::多边形名称
  3	播放段落 Triangle ::三角三角形
  4	播放段落 Quadrilateral ::四方
  5	播放段落 Pentagon ::五角大楼
  6	播放段落 Hexagon ::六边形
  7	播放段落 Heptagon ::七边形
  8	播放段落 Octagon ::八角
  9	播放段落 Nonagon (or enneagon) ::非agon( 或 ennagon)
  10	播放段落 Decagon ::十角

  播放段落

  For a polygon with more than 10 sides, most people prefer to name it by the number of sides and the suffix “gon.” For example, a 40-sided polygon would be a “40-gon.”
  ::对于一个有十面以上的多边形,大多数人更喜欢用边数和后缀“g”来命名它。 比如,40面多边形就是“40角 ” 。

  ---

  播放段落

  Convex Polygon
  ::Convex 多边形

  播放段落

  A diagonal is a line segment that connects any two non-adjacent vertices of a polygon. A polygon is convex if all diagonals remain inside the polygon. Most polygons that you study in high school geometry will be convex .
  ::对角线是一个连接多边形任何两个非相邻的顶点的线条段。如果所有对角线都留在多边形内,则多边形就是方形。在高中几何学中学习的大多数多边形都是正方形。

  播放段落

  Concave Polygon
  ::凝聚多边形

  播放段落

  If a polygon is not convex then it is concave (or non-convex). Some diagonals of a concave polygon lie partly or wholly outside the polygon.
  ::如果多边形不是二次曲线,则是二次曲线(或非一次曲线)。

  ---

  播放段落

  Regular Polygon
  ::经常多边形

  播放段落

  A polygon is equilateral if all of its sides are the same length. A polygon is equiangular if all of its angles are the same measure . A polygon is regular if it is both equilateral and equiangular.
  ::如果多边形的两边的长度相同,则多边形是等边。如果多边形的所有角度都是相同的度量,则多边形是等角。如果多边形既是等边的,又是等角的,则多边形是普通的。

  ---

  播放段落

  Exploring Polygons
  ::探索多边形

  播放段落

  Click the small blue arrow next to the image below and observe the different polygons, from triangles and up, by adding or removing sides. Explore the angles and lengths for by dragging any of the vertices of the polygon.
  ::单击下方图像旁边的蓝色小箭头,从三角形和向上观察不同的多边形,从三角形和向上,通过添加或删除侧面。通过拖曳多边形的任何顶点来探索角和长度。

  播放段落

  Note: You can alternate between regular and irregular polygons by check-marking the "Regular" box.
  ::注意: 您可以在常规多边形和非常规多边形之间通过检查标记“ Regular” 框进行交替。

  ---

  播放段落

  Sum of Interior Angles of a Polygon
  ::多边形的内部角和数

  播放段落

  The sum of the measures of the three angles in a triangle is 180 degrees. You can use this fact to find the sum of the measures of the angles in any polygon.
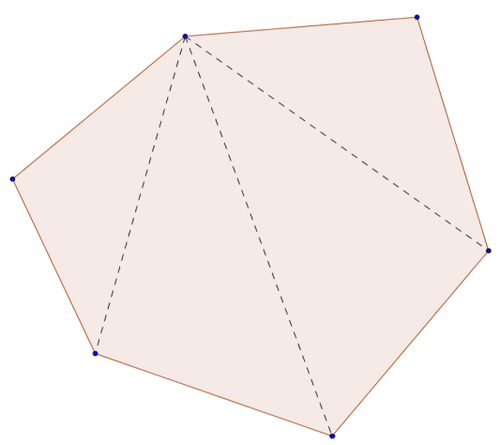
  ::三角形中三个角度的测量总和为 180 度。您可以使用这个事实在任何多边形中找到角的测量总和。

  播放段落

  For example, a  5-sided  pentagon   may be divided (or dissected ) ,  into three triangles, such that all the triangles are non-overlapping pieces and the interior angles have been marked. The sum of the measures of the angles of each triangle is $\begin{array}{r}{180}^{\circ }.\end{array}$  Therefore, the sum of the interior angles of  a regular pentagon is $\begin{array}{r}{180}^{\circ }\cdot 3={540}^{\circ }.\end{array}$
  ::例如,五面形的五面形可以分为(或解剖)三个三角形,这样所有三角形都是非重叠的片段,内部角已被标记。每个三角形角的测量总和是180。因此,普通五面形的内部角的总和是1803=540。

  播放段落

    General Rule:
  ::一般规则:

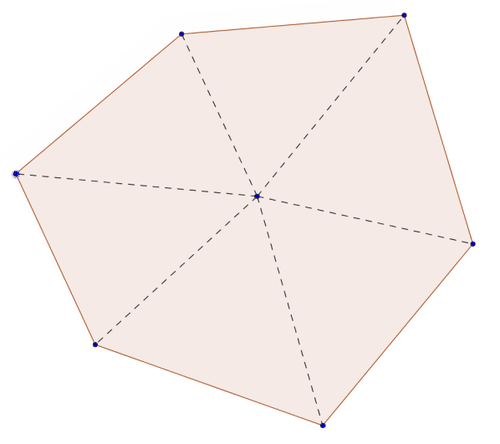
  播放段落

  A polygon of n-sides can be divided into (n-2) triangles .
  ::正侧多边形可分为(n-2)三角形。

  播放段落

  Therefore, the sum of all the interior angles of an n-sided polygon  $\begin{array}{r}=(n-2)\cdot {180}^{\circ }\end{array}$
  ::因此,正向多边形(n-2)的所有内角之和等于(n-2)180

  播放段落

  CK-12 Interactive: Polygons
  ::CK-12 互动:多边形

  

  INTERACTIVE

  Polygons

  

  播放段落

  Move the red points into the red circles to see the diagonals of the polygons.
  ::将红点移动到红圆,以查看多边形的对角。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  播放段落

  As a general rule, if a polygon is regular (and thus equiangular), you can figure out the measure of each interior angle by dividing the shape into triangles.
  ::作为一般规则,如果多边形是常规的(并因此是等角),您可以通过将形状分为三角形来找出每个内角的度量。

  ---

  播放段落

  Naming Polygons
  ::命名多边形

  播放段落

  For the heptagon given below, find the sum of the interior angles .
  ::对于下文给出的七边形,请找到内角的总和。

  播放段落

  Remember that each triangle  contributes 180 degrees to the measure of the heptagon. (If this seems confusing, notice that all of the angles in each triangle are included in the interior angles of the heptagon.)
  ::记住每个三角向七边形的度量贡献180度。 (如果这看起来令人困惑, 请注意每个三角形的所有角度都包含在七边形的内部角中 。)

  播放段落

  The sum of the interior angles of a heptagon is .
  ::七边形的内角之和是 。

  ---

  播放段落

  Measuring Interior Angles of a Polygon
  ::多边形测量内部角

  播放段落

  Find the measure of each  interior angle of a regular heptagon.
  ::查找正则七边形的每个内角的量度。

  播放段落

  Because  it is a regular heptagon , it is equiangular. That means each of the seven interior angles has the same measure.
  ::因为它是一个普通的七边形, 它是一个正方形。 这意味着七个内部角度的每个角度都有相同的量度 。

  播放段落

  The sum of the interior angles  is   $\begin{array}{r}{900}^{\circ }\end{array}$  (as demonstrated above).
  ::内角的总和为900(如上所示)。

  播放段落

  E ach of the seven interior angles is $\begin{array}{r}\frac{{900}^{\circ }}{7}\approx {128.6}^{\circ }.\end{array}$
  ::七个内部角度各为9007128.6。

  播放段落

      General Rule:
  ::一般规则:

  播放段落

  The measure of each interior angle of an equiangular n-gon is:
  ::度量方形正方形内角的每个内角是:

  播放段落

  $$\begin{array}{r}\frac{(n-2)\cdot {180}^{\circ }}{n}\end{array}$$

  
  :n-2) --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

  ---

  播放段落

  Examining the Relationship Between Angles of a Polygon
  ::检查多边形角度之间的关系

  播放段落

  An exterior angle is an angle between one side of a polygon and the extension of an adjacent side. In the polygon below, an exterior angle has been marked at vertex $\begin{array}{r}G\end{array}$ . How are exterior angles related to interior angles? What is the measure of the exterior angle at $\begin{array}{r}G?\end{array}$
  ::外部角是多边形一面与相邻侧延伸之间的角。 在下面的多边形中,外角被标记为顶点G。 外部角度与内角的关系如何? G 的外角的测量值是多少?

  播放段落

  The exterior angle and interior angle at the same vertex will always be supplementary because together they form a straight angle . In this case, the interior angle at point $\begin{array}{r}G\end{array}$ was approximately $\begin{array}{r}{128.6}^{\circ },\end{array}$ therefore the exterior angle is $\begin{array}{r}{180}^{\circ }-{128.6}^{\circ }={51.4}^{\circ }.\end{array}$
  ::同一顶端的外角和内角总是补充性的,因为它们共同形成一个直角。 在这种情况下,G点的内角约为128.6,因此外角为180128.651.4。

  ---

  播放段落

  Sum of Exterior Angles of a Polygon
  ::多边形外部角和

  播放段落

  The sum of the exterior angles of any polygon is $\begin{array}{r}{360}^{\circ }.\end{array}$  How is  that possible?
  ::任何多边形外角的总和是360 。 这怎么可能?

  播放段落

  There are many ways to think about the sum of the exterior angles of a polygon. One way is to first consider that the sum of all the straight angles through the vertices is $\begin{array}{r}180n^{\circ }\end{array}$ (where $\begin{array}{r}n\end{array}$ is the number of sides of the polygon).
  ::有很多方法可以思考多边形外部角度的总和。 一种方法是首先考虑通过顶端的所有直角的总和是180n( 其中n是多边形边数 ) 。

  播放段落

  If you only want the sum of the exterior angles , you must subtract the sum of the interior angles. Recall from above that the sum of the interior angles is $\begin{array}{r}180(n-2{)}^{\circ }.\end{array}$
  ::如果您只想要外部角度的总和,则必须减去内部角度的总和。从上面回顾,内部角度的总和是 180(n-2)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  The sum of the exterior angles = (sum of straight angles − sum of interior angles)
  ::外部角度的总和=(直角和内角总和)

  ---

  播放段落

  CK-12 Interactive: Polygons
  ::CK-12 互动:多边形

  ---

  播放段落

  Polygons - Examples
  ::多边形 - 示例

  播放段落

  Example 1
  ::例1

  播放段落

  Find the sum of the interior angles of a nonagon.
  ::查找非agon 的内角之和。

  播放段落

    $\begin{array}{rl}& \text{ Sum of the interior angles of a nonagon}\\ & =(n-2){180}^{\circ }\\ & =(9-2){180}^{\circ }\\ & =7\cdot {180}^{\circ }\\ & ={1260}^{\circ }\end{array}$
  ::非角的内角总和=(n-2)180(9-2)18071801260

  播放段落

  Example 2
  ::例2

  播放段落

  Find the measure of one interior angle of a regular nonagon.
  ::查找正则非角的一个内角的量度。

  播放段落

    $\begin{array}{rl}& \text{Each interior angle of a nonagon}\\ & =\frac{\text{sum of interior angles}}{\text{number of sides}}\phantom{\int }\\ & =\frac{{1260}^{\circ }}{9}\phantom{\int }\\ & ={140}^{\circ }\end{array}$
  ::非正方形的每个内角=内角之和 侧数= 12609140

  播放段落

  Example 3
  ::例3

  播放段落

  Find the measure of one exterior angle of a regular decagon.
  ::查找普通十角形外角的度量。

  播放段落

    $\begin{array}{rl}& \text{Each exterior angle of a decagon}\\ & =\frac{\text{sum of exterior angles}}{\text{number of sides}}\phantom{\int }\\ & =\frac{{360}^{\circ }}{10}\phantom{\int }\\ & ={36}^{\circ }\end{array}$
  ::十角的每个外角 = 外角之和 边数 3601036

  ---

  播放段落

  CK-12 PLIX Interactive: Exterior Angles in Convex Polygons
  ::CK-12 PLIX 交互作用: Convex 多边形中的外部角

  Summary

  播放段落 A polygon is convex if all diagonals remain inside the polygon. ::如果所有对角都留在多边形内,多边形就是正方形。 播放段落 A polygon is concave if some or all of its diagonals lie partly or wholly outside the polygon. ::多边形如果部分或全部处于多边形之外或完全处于该多边形之外,则该多边形即为二次曲线。 播放段落 A polygon is regular if it is both equilateral and equiangular. ::多边形如果既为等边形,又为等角,则为常规形。 播放段落 The sum of all interior angles of an n-sided polygon   $\begin{array}{r}=(n-2)\cdot 180°.\end{array}$   ::n-面多边形=(n-2)-180°的所有内角之和。 播放段落 The measure of each interior angle of an equiangular n-gon is: $\begin{array}{r}\frac{(n-2)\cdot 180°}{n}.\end{array}$   ::等角正方形的每个内角的测量量为n-2)180°n。 播放段落 The exterior angle and interior angle at the same vertex will always be supplementary. ::同一顶点的外角和内角始终是补充的。 播放段落 The sum of all the exterior angles of any polygon is 360°. ::任何多边形的所有外部角度的总和是360°。

  ---

  播放段落

  Reviews
  ::审查

  播放段落

  1. What is the measure of an exterior angle of a regular 45-gon?
  ::1. 普通的45角外角的量度是多少?

  播放段落

  2. What is the sum of the interior angles of a 35-gon?
  ::2. 35角的内角和内角是多少?

  播放段落

  3. Draw an example of a convex polygon and a concave polygon.
  ::3. 绘制一个锥形多边形和一个锥形多边形的示例。

  播放段落

  4. What is the name of a polygon with 8 sides?
  ::4. 8边多边形的名称是什么?

  播放段落

  5. What is the name of a polygon with 10 sides?
  ::5. 10边多边形的名称是什么?

  播放段落

  6. What is the name of a polygon with 4 sides?
  ::6. 有四面的多边形的名称是什么?

  播放段落

  7. How could you use the dissection shown in the picture below to show why the sum of the interior angles of a hexagon is $\begin{array}{r}{720}^{\circ }?\end{array}$
  ::7. 您如何使用下图所示的解剖来显示六边形内角的总和为何是720?

  

  播放段落

  8. How could you use the dissection shown in the picture below to show why the sum of the interior angles of a hexagon is $\begin{array}{r}{720}^{\circ }?\end{array}$
  ::8. 如何用下图所示的解剖来说明六边形内角的总和为何是720?

  

  播放段落

  9. A regular polygon has an interior angle of $\begin{array}{r}{150}^{\circ }.\end{array}$  How many sides does the polygon have?
  ::9. 普通多边形的内角为150。多边形有多少边?

  播放段落

  10. How could you use exterior angles to help you find the answer to question 9 ?
  ::10. 你如何利用外部角度帮助你找到问题9的答案?

  播放段落

  11. What is the sum of the exterior angles of an 11-gon?
  ::11. 11角外角的外角之和是多少?

  播放段落

  12. What is the sum of the interior angles of an 11-gon?
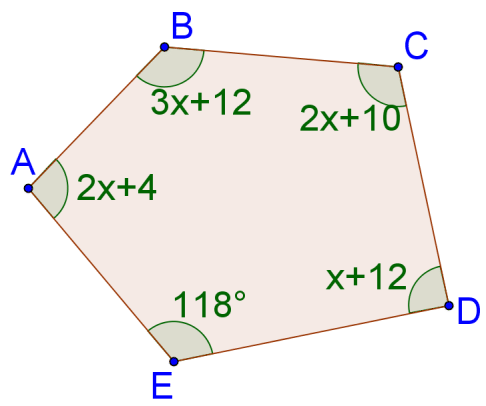
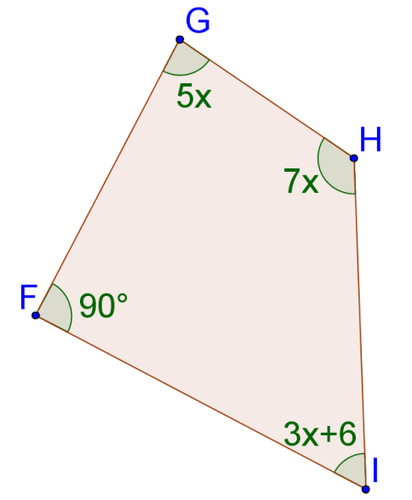
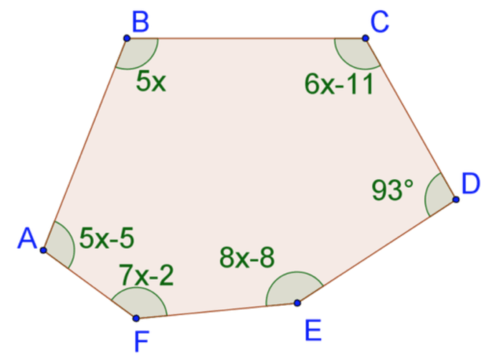
  ::12. 11角内角的内角之和是多少?

  播放段落

  13. Solve for $\begin{array}{r}x:\end{array}$
  ::13. 解决x:

  

  播放段落

  14. Solve for $\begin{array}{r}x:\end{array}$
  ::14. 解决x:

  

  播放段落

  15. Solve for $\begin{array}{r}x:\end{array}$
  ::15. 解决x:

  

  播放段落

  16. Draw a regular polygon that has more than 5 sides. Find the measure of one interior angle using two different methods. Explain which one you prefer and why.
  ::16. 绘制一个有5个以上边的正多边形。用两种不同的方法查找一个内角的量度。请解释您喜欢哪种和为什么。

  播放段落

  17. Is it possible to draw a regular polygon that cannot  be decomposed into triangles? Why or why not?
  ::17. 是否有可能绘制一个无法分解成三角形的正多边形?为什么或为什么没有?

  播放段落

  18. What is the shape of a polygon that has an infinite number of sides? Why? 
  ::18. 多边形的形状是什么,其边数是无限的?为什么?

  播放段落

  19. How many diagonals can be drawn in a triangle? A quadrilateral? A pentagon? Continue the experiment and explain the pattern.
  ::19. 三角形中可以绘制多少对角线? 四边形? 五边形? 继续实验并解释图案。

  播放段落

  20. Jerome  claims that he can completely cover his bathroom floor with rectangular tiles, without any gaps or overlaps. Halle  claims she can do the same with equilateral triangles. Who is correct and why? Experiment to see if there are other shapes that can be used to tile the floor without gaps or overlaps. Explain your results. 
  ::20. Jerome声称,他可以用长方形瓷砖完全覆盖他的浴室地板,而没有任何空白或重叠。Halle声称,她也可以用等边三角形来覆盖他的浴室地板。谁是正确的,为什么?实验看看是否有其他形状可以用来在没有空白或重叠的情况下平铺地板。请解释你的结果。

  播放段落

  21. Daniel claims that he's created a regular polygon whose interior angles measure  $\begin{array}{r}{142}^{\circ }.\end{array}$ Is his claim true? Explain.
  ::21. 丹尼尔声称,他创造了一个常规多边形,其内部角度测量142。他的说法是真的吗?解释一下。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。