1.4 三角-定义、分类、互动和实例-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节三角形 - 定义、分类、互动和实例

  折叠 展开

  三角形 - 定义、分类、互动和实例

  播放段落

  What is a Triangle?
  ::什么是三角形?

  播放段落

  A triangle is any closed figure made by three non- parallel line segments. Triangles can be classified by their sides and by their angles .
  ::三角形是指由三个非平行线段组成的任何封闭数字。三角形可以按其侧面和角度进行分类。

  播放段落

  Triangle Classification Based on Sides
  ::三角按侧面划分的三角分类

  播放段落

  When classifying a triangle by its sides, determine if any of the sides are the same length. If no sides are the same length, then it is a scalene triangle . If two sides are the same length, then it is an isosceles triangle . If all three sides are the same length, then it is an equilateral triangle . You can show that two sides are the same length by drawing tick marks through the middle of the sides. Sides with a corresponding number of tick marks are the same length.
  ::将三角形按其侧侧进行分类时, 确定任何边的长度是否相同。 如果没有两边的长度相同, 则将是一个缩放三角形。 如果两边的长度相同, 则将是一个等星三角形。 如果三边的长度相同, 则将是一个等星三角形。 您可以在两边中间划勾, 显示两边的长度相同。 带有相应数的勾标记的边的长度相同 。

  ---

  播放段落

  Triangle Classification Based on Angles
  ::基于角度的三角分类

  播放段落

  You can also classify a triangle by assessing the sizes of its angles. If there is a right angle (a $\begin{array}{r}{90}^{\circ }\end{array}$ angle), then it is a right triangle . If the measures of all angles are less than $\begin{array}{r}{90}^{\circ }\end{array}$ , then it is an acute triangle . If the measure of one angle is greater than $\begin{array}{r}{90}^{\circ }\end{array}$ , then it is an obtuse triangle .
  ::您也可以通过评估三角形角度的大小来对三角形进行分类。如果有一个右角(a 90angle),那么它就是右三角形。如果所有角的测量值小于90,那么它就是急性三角形。如果一个角的测量值大于90,那么它就是隐形三角形。

  播放段落

  The sum of the measures of the interior angles of any triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ . If the three angles of a triangle are all the same, then the triangle is an equiangular triangle and each angle measure is $\begin{array}{r}{60}^{\circ }\end{array}$ . are always equiangular and vice versa. In fact, the number of sides that are the same length will always correspond to the number of angles that are the same measure.
  ::任何三角形内角的测量总和为 180 。 如果三角形的三个角度完全相同, 那么三角形就是一个等角三角形, 每个角度量为 60 。 总是 等角, 反之亦然。 事实上, 相同长度的边数总是与相同度量的角数相对应 。

  ---

  播放段落

  Can an obtuse triangle sometimes be an equilateral triangle?
  ::隐形三角形有时会不会是等边三角形?

  播放段落

  It is for an obtuse triangle to sometimes be an equilateral triangle.
  ::隐形三角形有时会变成等边三角形。

  播放段落

  CK-12 Interactive: Triangles
  ::CK-12 互动:三角

  ---

  播放段落

  Sample Classifications of Triangles
  ::三角的分类

  播放段落

  Obtuse isosceles triangle
  ::阻力等离子三角形

  

  播放段落

  This triangle has two sides that are congruent (the same length), so it is isosceles. More specifically, it also has one angle that is greater than $\begin{array}{r}{90}^{\circ }\end{array}$ , so it is obtuse.
  ::此三角形的两边是相同的( 相同的长度) , 所以是等分形 。 更具体地说, 它还有一个大于 90 的角, 所以是隐蔽的 。

  播放段落

  Scalene right triangle
  ::缩缩右三角形

  播放段落

  The measures of two angles of a triangle are $\begin{array}{r}{30}^{\circ }\end{array}$ and $\begin{array}{r}{60}^{\circ }\end{array}$ . What type of triangle is it?
  ::三角形的两个角度的度量是 30 和 60 。 它是什么类型的三角形 ?

  播放段落

  Let the third angle be ' $\begin{array}{r}x\end{array}$ '.
  ::第三个角度应该是“x”。

  播放段落

  We know that the sum of the measures of the interior angles of any triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::我们知道,任何三角形内角的测量总和是180。

  播放段落

  $\begin{array}{rl}{30}^{\circ }+{60}^{\circ }+x& ={180}^{\circ }\\ {90}^{\circ }+x& ={180}^{\circ }\\ x& ={180}^{\circ }-{90}^{\circ }\\ x& ={90}^{\circ }\end{array}$
  ::3060x=180 90x=180x=180}90x=90*

  播放段落

  One angle is a right angle, so this is a right triangle . More specifically, all of the angles are different measures (which only happens when all sides are different lengths), so this is a scalene right triangle.
  ::一个角度是一个右角度, 因此这是一个右三角形。 更具体地说, 所有角度都是不同的度量( 只有当所有边的长度不同时才发生) , 所以这是一个缩放右三角形 。

  ---

  ---

  播放段落

  Triangles - Examples
  ::三角三角形 - 示例

  播放段落

  Example 1
  ::例1

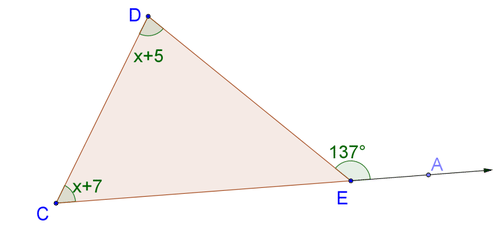
  播放段落

  How is an exterior angle of a triangle related to the interior angles of the triangle? In the triangle below, how is exterior angle $\begin{array}{r}\mathrm{\angle }BCE\end{array}$ related to interior angles $\begin{array}{r}\mathrm{\angle }A\end{array}$ and $\begin{array}{r}\mathrm{\angle }B\end{array}$ ?
  ::三角形的外部角与三角形的内部角有何关联? 在下三角形中, 外部角 BCE 与内部角 A 和 B 有何关联?

  播放段落

  T he sum of the measures of the interior angles of any triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::任何三角形内角的测量总和为180。

  播放段落

  In $\begin{array}{r}\mathrm{△}ABC\end{array}$ ,
  ::在ABC,

  播放段落

  $\begin{array}{rl}m\mathrm{\angle }A+m\mathrm{\angle }B+m\mathrm{\angle }BCA& ={180}^{\circ }\\ m\mathrm{\angle }ECB+m\mathrm{\angle }BCA& ={180}^{\circ }[\text{ linear pair }]\end{array}$
  ::mA+mB+mBCA=180mECB+mBCA=180[线性对

  播放段落

  Since both angle sums are equal to 180 degrees, they are both equal to each other:
  ::由于角数均等于180度,因此两者对等:

  播放段落

  $\begin{array}{rl}m\mathrm{\angle }A+m\mathrm{\angle }B+m\mathrm{\angle }BCA& =m\mathrm{\angle }BCA+m\mathrm{\angle }ECB\\ m\mathrm{\angle }A+m\mathrm{\angle }B& =m\mathrm{\angle }ECB\end{array}$
  ::mA+mB+mBCA=mBCA+mECB_BMA+mB=mEECB

  播放段落

  In general, the measure of an exterior angle of a triangle will always be equal to the sum of the measures of the other two interior angles.
  ::一般而言,三角形外角的测量量总是等于其他两个内角的测量量的总和。

  播放段落

  Example 2
  ::例2

  播放段落

  The measures of two angles of a triangle are $\begin{array}{r}{45}^{\circ }\end{array}$ and $\begin{array}{r}{45}^{\circ }\end{array}$ . What type of triangle is it?
  ::三角形两个角度的度量是 4545454545。 三角形是哪种类型 ?

  播放段落

  Let the third angle be ' $\begin{array}{r}x\end{array}$ '.
  ::第三个角度应该是“x”。

  播放段落

  We know that the sum of the measures of the interior angles of any triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::我们知道,任何三角形内角的测量总和是180。

  播放段落

  $\begin{array}{rl}{45}^{\circ }+{45}^{\circ }+x& ={180}^{\circ }\\ {90}^{\circ }+x& ={180}^{\circ }\\ x& ={180}^{\circ }-{90}^{\circ }\\ x& ={90}^{\circ }\end{array}$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}45*45**45**x=180*90*x=180*x=180**90*x=90**

  播放段落

  One angle is a right angle, so this is a right triangle. Because two angles are the same measure, two sides must be the same length. Therefore, it is an isosceles triangle .
  ::一个角度是一个右角度, 因此这是一个右三角形。 因为两个角度是相同的度量, 两边必须是相同的长度。 因此, 它是一个等分三角形 。

  播放段落

  Example 3
  ::例3

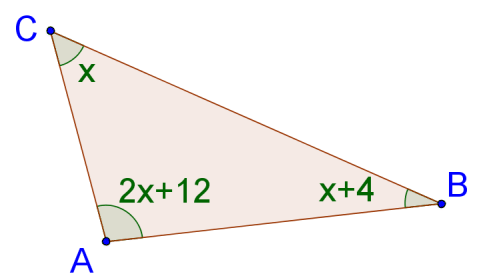
  播放段落

  Solve for $\begin{array}{r}x\end{array}$ (the picture is not drawn to scale). Find the measure of each angle from $\begin{array}{r}\mathrm{△}HIJ\end{array}$ .
  ::解析 x (图片不绘制为缩放) 。 从 QHIJ 中查找每个角度的量度 。

  

  播放段落

  T he sum of the measures of the interior angles of any triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::任何三角形内角的测量总和为180。

  播放段落

  In $\begin{array}{r}\mathrm{△}HIJ\end{array}$ ,
  ::在'HIJ'中,

  播放段落

  $\begin{array}{rl}\mathrm{\angle }HIJ+\mathrm{\angle }IJH+\mathrm{\angle }JHI& ={180}^{\circ }\\ (3x-4)+x+(2x+5)& =180\\ 6x+1& =180\\ 6x& =180-1\\ x& =\frac{179}{6}=29.8\\ m\mathrm{\angle }IJH& =x={29.8}^{\circ }\\ m\mathrm{\angle }HIJ& =3x-4=3(29.8)-4={85.5}^{\circ }\\ m\mathrm{\angle }JHI& =2x+5=2(29.8)+5={64.7}^{\circ }\end{array}$
  ::HIJIJJH=180(3x-4)+x+(2x+5)=1806x+1=1806x=180-1x=1796=29.8mIJH=x=29.8mHIJ=3x-4=3(29.8)-4=85.5mJHI=2x+5=2(29.8)+5=64.7

  播放段落

  Example 4
  ::例4

  播放段落

  Which side of $\begin{array}{r}\mathrm{△}HIJ\end{array}$ is longest? Which side is shortest? The image is drawn to scale.
  ::QHIJ 的哪一边最长? 哪一边最短? 图像被画成比例 。

  

  播放段落

  The question states that the image is drawn to scale, and v isually, the largest angle is $\begin{array}{r}\mathrm{\angle }I,\end{array}$ so the longest side must be the side created by $\begin{array}{r}\mathrm{\angle }I,\end{array}$ which is $\begin{array}{r}\overline{JH}.\end{array}$ The shortest side is across from the smallest angle. The smallest angle is $\begin{array}{r}\mathrm{\angle }J,\end{array}$ so the shortest side is $\begin{array}{r}\overline{IH}.\end{array}$
  ::问题指出,图像被画成比例,视觉上最大的角是“I”,所以最长的一面必须是“I”创造的一面,即JH。最短的一面是最小的一面。最小的一面是“J”,所以最短的一面是“I”。

  ---

  播放段落

  CK-12 PLIX Interactive: Triangle Classification by Side Lengths
  ::CK-12 PLIX 互动:按边长的三角分类

  Remember this!

  播放段落 Triangles can be classified by their sides and by their angles: 播放段落 Scalene triangles have no sides that are the same length. ::缩放三角形没有长度相同的边。 播放段落 Isosceles triangles have two sides that are the same length. ::Isoseles三角形的两边长度相同。 播放段落 Equilateral triangles have all three sides that are the same length. ::等边三角形的三边长度相同。 播放段落 Right triangles have one angle that measures exactly 90°. ::右三角形有一个角度,可以精确测量90度。 播放段落 Acute triangles have all angles that measure less than 90°. ::急性三角形的所有角度均测量不到90度。 播放段落 Obtuse triangles have one angle that measures greater than 90°. ::阻塞三角形有一个角度,测量度大于90度。 ::三角形可以按其侧面和角度进行分类: 斜角三角形没有长度相同的边。 等角三角形有长度相同的两边。 等角三角形有长度相同的所有三边。 右三角形有一个角度, 精确测量90度。 急性三角形有测量度低于90度的所有角度。 硬三角形有一个角度, 测量度大于90度。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. What are the three ways to classify a triangle by its sides?
  ::1. 按三角形两侧划分三角形的三种方式是什么?

  播放段落

  2. What are the four ways to classify a triangle by its angles?
  ::2. 按三角角对三角形进行分类的四种方式是什么?

  播放段落

  3. Can a right triangle be equiangular? Explain.
  ::3. 右三角能否是等角?解释一下。

  播放段落

  4. The measures of two angles of a triangle are $\begin{array}{r}{42}^{\circ }\end{array}$ and $\begin{array}{r}{42}^{\circ }\end{array}$ . What type of triangle is it?
  ::4. 三角形两个角度的度量是42°和42°。

  播放段落

  5. The measures of two angles of a triangle are $\begin{array}{r}{120}^{\circ }\end{array}$ and $\begin{array}{r}{12}^{\circ }\end{array}$ . What type of triangle is it?
  ::5. 三角形的两个角度是120°和12°。

  播放段落

  6. Solve for $\begin{array}{r}x\end{array}$ (the picture is not drawn to scale).
  ::6. 解决 x (图片不绘制为缩放) 。

  

  播放段落

  7. Find the measure of each angle for $\begin{array}{r}\mathrm{△}ABC\end{array}$ in #6.
  ::7. 在#6中查找 ABC 的每个角度的量度。

  播放段落

  8. Solve for $\begin{array}{r}x\end{array}$ (the picture is not drawn to scale). Round your answer to the nearest hundredths place.
  ::8. 解答 x (图片不缩放) 。 将您的答案绕到最接近的百位 。

  

  播放段落

  9. Using your answer from #8, find the measure of each angle for the triangle.
  ::9. 利用8号的回答,找到三角形每个角度的度量。

  播放段落

  10. Which side $\begin{array}{r}\mathrm{△}DEF\end{array}$ of from #8 is the longest? Which side of $\begin{array}{r}\mathrm{△}DEF\end{array}$ is the shortest? How do you know?
  ::10. 从8号站到哪边是最长的?“DEF”的哪一边是最短的?你怎么知道?

  播放段落

  11. Use the angle measurements to order the sides of the triangle below from shortest to longest.
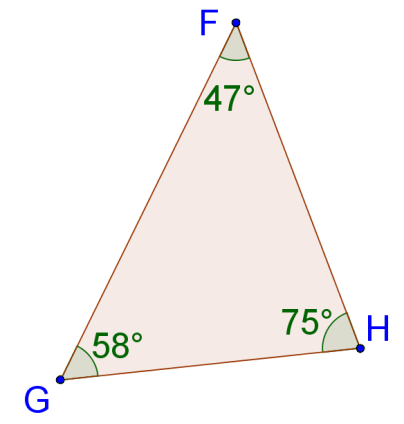
  ::11. 使用角测量法将三角形下方的边从最短到最长排列。

  

  播放段落

  12. Use the side measurements to order the measures of the angles in the triangle below from smallest to largest.
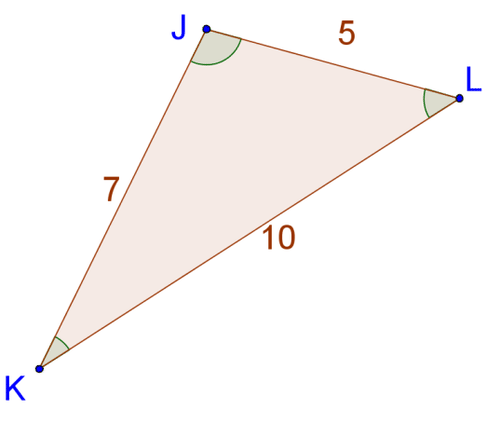
  ::12. 使用侧边测量方法,将三角形下角的测量线从最小到最大。

  

  播放段落

  13. One of the exterior angles of a triangle is $\begin{array}{r}{100}^{\circ }\end{array}$ . What do you know about the interior angles?
  ::13. 三角形的外角之一是100。你对内角了解多少?

  播放段落

  14. Solve for $\begin{array}{r}x\end{array}$ (the picture is not drawn to scale).
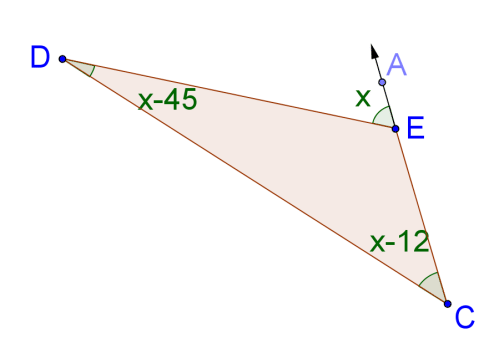
  ::14. 解决 x (图片不绘制成比例) 。

  

  播放段落

  15. Determine $\begin{array}{r}x,\end{array}$  then use it to find $\begin{array}{r}m\mathrm{\angle }DEC\end{array}$ (the picture is not drawn to scale).
  ::15. 确定 x, 然后用它来查找 mçDEC( 图片不绘制为缩放) 。

  

  播放段落

  16. In an equilateral triangle, all the sides are equal in the length and all the angles have equal measure. If we alter one angle of an equilateral triangle, what must happen to the side opposite? Is it always true that the longest side of a scalene triangle is opposite the largest angle? Why or why not?
  ::16. 在等边三角形中,所有两边的长度相等,所有角度的量度相等;如果我们改变一个等边三角形的一个角度,那么另一边会发生什么情况?比例三角形最长的一面与最大的角度对立,这是否始终属实?为什么或为什么不是?

  播放段落

  17. Using a diagram, explain why the measure of an exterior angle of a triangle is the sum of the measures of the two remote interior angles.
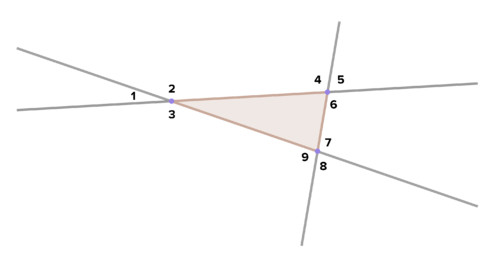
  ::17. 使用图表,解释三角形外角的测量值为何是两个边远内角的测量值之和。

  播放段落

  18. Frasier argues that every angle labeled below is an exterior angle of the triangle. Is he correct? Why or why not?
  ::18. Frasier认为,下面标明的每一个角都是三角形的外角,他正确吗?为什么或为什么没有?

  

  播放段落

  19. Draw a triangle with vertex A, along with the two exterior angles whose vertex is A. There are 3 angles that share vertex A. What is the sum of all these angles? True or False: Each of the angles around vertex A is either the sum of angles of the triangle or equal to an angle of the triangle. Is this also the case for the remaining vertices of the triangle? Explain.
  ::19. 绘制一个带有顶点A的三角形,以及两个外向角度的顶点为 A。 共有3个角度, 共有顶点A。 所有这些角度的总和是多少? 真实还是假: 顶点A周围的每个角度要么是三角形角度的总和,要么等于三角形的一个角度。 三角形其余的顶点是否也属于这种情况? 请解释 。

  播放段落

  20. Sketch a scalene triangle and make 5 copies, then cut them out. Is it possible to arrange these 6 triangles so that they all share one vertex? Does the resulting arrangement cover a surface without gaps, and without overlapping triangles? What characteristic of the angles around the vertex of a triangle makes this possible? Explain.
  ::20. 绘制一个缩放三角形并制作5份副本,然后将其切除;能否安排这6个三角形,以便它们都共用一个顶点?由此产生的安排是否覆盖一个没有空白的表面,没有重叠的三角形?三角形周围角的特征是什么?解释一下。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。