1.10 固体数量 -- -- 定义、公式、互动和实例-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 固体数量 - 定义、公式、互动和实例

  Collapse Expand

  固体数量 - 定义、公式、互动和实例

  播放段落

  What is Volume of a Solid?
  ::什么是固体量?

  播放段落

  The volume of a solid is the measure of how much space an object takes up. It is measured by the number of unit cube s it takes to fill up the solid. 
  ::固态体积是测量一个物体所占用空间的大小。它用填充固体所需的单位立方体数量来衡量。

  播放段落

  Counting the unit cubes in the solid, we have 30 unit cubes, so the volume is: 2 units $\begin{array}{r}\cdot \end{array}$ 3 units $\begin{array}{r}\cdot \end{array}$ 5 units = 30 cubic units .
  ::在计算固体中的单位立方体时, 我们有30个单位立方体, 所以体积是: 2 单位+3 单位+5 单位= 30 立方单位。

  播放段落

  CK-12 Interactive: Volume of Solids
  ::CK-12 互动:固体量

  

  INTERACTIVE

  Volume of Solids

  

  播放段落

  Move the red point to change the volume of the square pyramid. Move the blue point to change the volume of the rectangular prism. Observe how the volume of the composite solid changes as the volumes of its components change.
  ::移动红色点以改变方形金字塔的体积。 移动蓝色点以改变矩形棱柱的体积。 观察复合固体的体积随其成分的体积变化如何 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  ---

  播放段落

  Volume of a Prism
  ::棱晶体体量

  播放段落

  A prism is a solid with two congruent polygon bases that are parallel and connected by rectangles . Prisms are named by their base shape .
  ::棱镜是一个固态,它有两个相似的多边形基点,它们与矩形平行并相连。棱镜按其底形命名。

  播放段落

  To find the volume of a prism , find the area of its base and multiply by its height .
  $\begin{array}{r}{V}_{\text{prism}}\end{array}$ $\begin{array}{r}=A_{\text{base}}\cdot h\end{array}$    
  ::要找到棱晶的体积, 找到基点的面积, 乘以它的高度 。 Vprism= Abaseh

  播放段落

  CK-12 Interactive: Volume of Solids
  ::CK-12 互动:固体量

  

  INTERACTIVE

  Volume of Solids

  

  播放段落

  Move the red point to explore the relationship between numbers of faces, vertices and edges in polyhedrons with different bases.
  ::移动红点以探索不同基点的多面圆形面、顶点和边缘的数量之间的关系。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  ---

  播放段落

  Volume of a Cylinder
  ::圆柱体体积

  播放段落

  A cylinder is a three-dimensional solid consisting of two congruent, parallel, circular sides (the bases ), joined by a curved surface .
  ::一个圆柱体是一个三维的固体,由两个平行的圆形两面(基)组成,并加上一个弯曲的表面。

  播放段落

  To find the volume of a cylinder , find the area of its circular base and multiply by its height.
  ::找到圆柱体的体积,找到圆柱体的圆基区域,乘以其高度。

  播放段落

  $\begin{array}{r}{V}_{\text{cylinder}}\end{array}$ $\begin{array}{r}=\pi r^{2}h\end{array}$
  ::Vcylinderr2h

  播放段落

  CK-12 PLIX: Surface Area and Volume of Cylinders
  ::CK-12 PLIX: 地表面积和气瓶体积

  ---

  播放段落

  Volume of a Pyramid
  ::金字塔体积

  播放段落

  A pyramid is a three dimensional solid with a polygonal base . Each corner of a polygon is attached to a singular vertex , which gives the pyramid its distinctive shape. Each base edge and the vertex form a triangle . Pyramids are named by their base shape .
  ::金字塔是三维固态,具有多边形基。多边形的每个角都附于一个单一的顶点上,使金字塔具有独特的形状。每个基边和顶点形成一个三角。金字塔按其底部形状命名。

  播放段落

  To find the volume of a pyramid, find the volume of the prism with the same base and divide by three. 
  ::要找到金字塔的体积, 找到基数相同的棱晶体积, 并除以三。

  播放段落

  $\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$
  ::Vpyramid=Abase_h3 甚金字塔=Abase_h3

  ---

  播放段落

  Volume of a Cone
  ::圆锥体的体积

  播放段落

  A cone is a three-dimensional solid with a circular base whose lateral surface meets at a point called the vertex .
  ::锥体是三维固态的圆形基体,其横向表面在一个称为顶点的地方相交。

  播放段落

  To find the volume of a cone, find the volume of the cylinder with the same base and divide by three.
  ::要找到锥体的体积,请找到基数相同、除以3的圆柱体体积。

  播放段落

  $\begin{array}{r}{V}_{\text{cone}}=\frac{\pi r^{2}h}{3}\end{array}$
  ::Vconer2h3

  播放段落

  Consider:
  ::考虑:

  播放段落

  What is the ratio between the volume of a cylinder and of a cone, having the same radius and height?
  ::圆柱体体积与圆锥体体体积之比是多少? 圆锥体的半径和高度相同?

  播放段落

  The ratio between the volume of a cylinder and a cone with the same radius and height is .
  ::圆柱体体积与圆锥体体体积之比,其半径和高度相同。

  ---

  播放段落

  Volume of a Sphere
  ::一个球体的音量

  播放段落

  A sphere is the set of all points in space equidistant from a center point . The distance from the center point to the sphere is called the radius .
  ::球体是指从中点到中点之间的空间等距的所有点。从中点到球体的距离称为半径。

  播放段落

  The volume of a sphere relies on its radius.
  ::球体的体积取决于它的半径

  播放段落

  $\begin{array}{r}{V}_{\text{sphere}}=\frac{4}{3}\pi r^3\end{array}$
  ::Vsphere = 43r3

  ---

  播放段落

  Calculating Volume
  ::计算音量

  播放段落

  Adjust the dimensions of the solid given below and observe how the volume changes.
  ::调整以下所列固体的尺寸,并观察体积的变化。

  播放段落

  Cone
  ::锥体

  ---

  播放段落

  Volume of a Composite Solid
  ::复合固体体积

  播放段落

  A composite solid is a solid made up of common geometric solids. The solids that it is made up of are generally prisms, pyramids, cones, cylinders and spheres.
  ::复合固体是由普通几何固体构成的固体,其构成的固体一般是棱晶、金字塔、锥形、圆柱体和球体。

  播放段落

  The volume of a composite solid is the sum of the volumes of the individual solids that make up the composite. 
  ::复合固体的体积是构成复合物的单个固体体积的总和。

  播放段落

  Let's look at some problems where we find the volume. 
  ::让我们看看我们找到音量的一些问题。

  播放段落

  1. Find the volume of the rectangular prism below. 
  ::1. 在以下查找矩形棱柱的体积。

  播放段落

  To find the volume of the prism, you need to find the area of the base and multiply by the height . Note that for a rectangular prism, any face can be the “base”, not just the face that appears to be on the bottom.
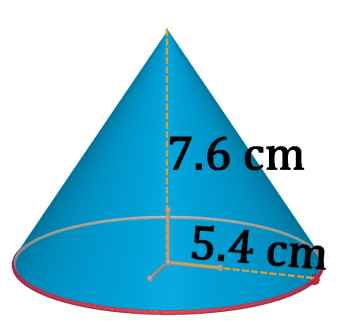
  ::要找到棱柱的体积, 您需要找到基点的面积, 并乘以高度。 请注意, 对于矩形棱柱来说, 任何面孔都可以是“ 底部” , 而不仅仅是看起来在底部的面孔 。

  播放段落

  2. Find the volume of the cone below.
  ::2. 在下文查找锥体的体积。

  播放段落

  To find the volume of the cone, you need to find the area of the circular base , multiply by the height , and divide by three.
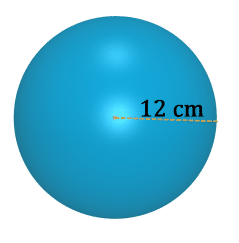
  ::要找到圆锥体的体积, 您需要找到圆圆基的面积, 乘以高度, 并除以 3 。

  播放段落

  3. Find the volume of a sphere with radius 4 cm.
  ::3. 查找四厘米半径的球体体积。

  播放段落

  $\begin{array}{rl}\text{Volume of Sphere}& =\frac{4}{3}\pi r^3\\ & =\frac{4}{3}\pi (4{)}^3\\ & =\frac{256\pi }{3}{\text{cm}}^3\end{array}$
  ::圆柱体体积=43°r3=43(4)3=2563立方厘米3

  ---

  播放段落

  Volume of Solids - Examples
  ::固体数量 -- -- 实例

  播放段落

  Example 1
  ::例1

  播放段落

  The composite solid below is made of a cube and a square pyramid . The length of each edge of the cube is 12 feet and the overall height of the solid is 22 feet. What is the volume of the solid? Why might you want to know the volume of the solid?
  ::下面的复合固体是由立方体和方形金字塔组成的。 立方体每个边缘的长度是12英尺, 固体的总高度是22英尺。 固体的体积是多少? 您为什么想知道固体的体积?

  播放段落

  To find the volume of the solid, find the sum of the volumes of the prism (the cube) and the pyramid. Note that since the overall height is 22 feet and the height of the cube is 12 feet, the height of the pyramid must be 10 feet.
  ::要找到固体的体积, 请找到棱晶( 立方体) 和金字塔的体积总和。 请注意, 由于整体高度为22英尺, 立方体的体高度为12英尺, 金字塔的高度必须是10英尺 。

  播放段落

  $$\begin{array}{rl}\text{Volume of Prism (Cube)}& =A_{\text{base}}\cdot h\\ & =(12\cdot 12)(12)\\ & =1728{\text{ft}}^3\\ \text{Volume of Pyramid}& =\frac{A_{\text{base}}\cdot h}{3}\\ & =\frac{(12\cdot 12)(10)}{3}\\ & =480{\text{ft}}^3\\ \text{Total Volume}& =\text{Volume of Prism (Cube)}+\text{Volume of Pyramid}\\ & =1728+480\\ & =2208{\text{ft}}^3\end{array}$$

  
  ::立方体积(立方体)=Abasih=(12)12(12)12(12)12=1728平方体积;金字塔=Abasih3=(12)12(10)3=480平方体积=480平方体积(立方体)+金字塔=1728+480=2208平方体

  播放段落

  The volume helps you to know how much the solid will hold. One cubic foot holds about 7.48 gallons of liquid, so
  ::体积能帮助你了解固体能承受多少。一个立方英尺能容纳大约7.48加仑的液体,所以

  播放段落

  $\begin{array}{rl}\text{Gallons of liquid the solid can hold }& =\text{ Volume of solid }\cdot \text{ Number of gallons/cubic foot}\\ & =(2208)(7.48)\\ & =16,515.84\text{gallons}\end{array}$
  ::固态固态所持液体加仑数 = 固体体积 + 磅/立方英尺数 = (2208) (7.48) = 16 515.84加仑

  播放段落

  Example 2
  ::例2

  播放段落

  The area of the base of the prism below is $\begin{array}{r}100{\text{cm}}^2\end{array}$ . The height is 5 cm. What is the volume of the prism?
  ::底部底部的底部区域是 100 cm 2。 高度是 5 cm。 棱晶的体积是多少 ?

  播放段落

  $\begin{array}{rl}{V}_{\text{prism}}& =A_{\text{base}}\cdot h\\ & =(100{\text{cm}}^2)\cdot (5\text{cm})\\ & =500{\text{cm}}^3\end{array}$
  ::Vprism=Abaseh=(100厘米2)(5厘米)=500厘米3

  播放段落

  Example 3
  ::例3

  播放段落

  The volume of a sphere is $\begin{array}{r}\frac{500\pi }{3}{\text{in}}^3\end{array}$ . What is the radius of the sphere?
  ::球体的体积是500°3 3英寸 球体的半径是多少?

  播放段落

  To find the radius, use the formula: Volume of Sphere =  $\begin{array}{r}\frac{4}{3}\pi r^3\end{array}$
  ::要找到半径, 请使用公式: 球体体积= 43°r3

  播放段落

                                                                                 $\begin{array}{rl}\frac{500\pi }{3}& =\frac{4}{3}\pi r^3\\ 4r^3& =500\\ r^3& =125\\ r& =5\text{in}\end{array}$
  ::5003=43r34r3=500r3=125r=5 英寸

  播放段落

  Example 4
  ::例4

  播放段落

  The volume of a square pyramid is $\begin{array}{r}64{\text{in}}^3\end{array}$ . The height of the pyramid is three times the length of a side of the base. What is the height of the pyramid? 
  ::平方金字塔的体积是64英寸。 金字塔的高度是基底侧的三倍。金字塔的高度是多少?

  播放段落

  Side  $\begin{array}{r}s=4\text{in}\end{array}$ and height  $\begin{array}{r}h=3(4)=12\text{in}.\end{array}$
  ::侧面=4 英寸 h=3(4)=12 英寸。

  Summary

  播放段落 Volume of a solid is the measure of how much space an object takes up, measured by the number of unit cubes it takes to fill up the solid. ::固体体积是测量一个物体占用多少空间的尺度,以它填充固体所需的单位立方体数量衡量。 播放段落 Volume of sphere $\begin{array}{r}=\frac{4}{3}\pi r^3\end{array}$   ::面积 = 43°r3 播放段落 Volume of a prism $\begin{array}{r}=A_{\text{base}}\cdot h\end{array}$   ::棱晶体积=Abase_h 播放段落 Volume of a pyramid $\begin{array}{r}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$   ::金字塔体积=Abase_h3 播放段落 Volume of a cone $\begin{array}{r}=\frac{\pi r^{2}h}{3}\end{array}$   ::圆锥体的体积 *°r2h3 播放段落 Volume of a cylinder $\begin{array}{r}=\pi r^{2}h\end{array}$   ::气瓶 °°°r2h 气瓶体积

  ---

  播放段落

  Volume of Solids - Review Questions
  ::固体数量----审查问题

  播放段落

  Find the volume of each solid or composite solid.
  ::查找每个固体或复合固体的体积。

  1. 

  

  2.

  

  3.

  

  4. 

  

  播放段落

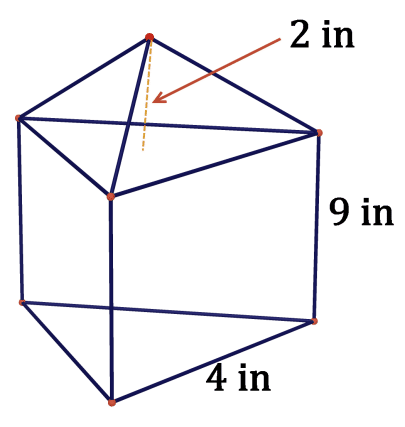
  5 . The base is an equilateral triangle.
  ::5. 基地是一个等边三角。

  

  6. 

  

  播放段落

  7. Explain why the formula for the volume of a prism involves the area of the base.
  ::7. 解释棱晶体积公式为何涉及基数区域。

  播放段落

  8. How is a cylinder related to a prism?
  ::8. 圆柱体如何与棱晶相关?

  播放段落

  9. How is a pyramid related to a cone?
  ::9. 金字塔如何与锥形相关?

  播放段落

  10. How is a sphere related to a circle?
  ::10. 一个领域与圆圈的关系如何?

  播放段落

  11. If one cubic centimeter will hold 1 milliliter of water, approximately how many liters of water will the solid in #1 hold? (One liter is 1000 milliliters).
  ::11. 如果一立方厘米能容纳1毫升水,1号水库中的固体能容纳大约多少升水? (一升是1000毫升)。

  播放段落

  12. If one cubic centimeter will hold 1 milliliter of water, approximately how many liters of water will the solid in #3 hold? (One liter is 1000 milliliters).
  ::12. 如果一立方厘米将持有1毫升水,3号水库中的固体将持有大约多少升水? (一升是1000毫升)。

  播放段落

  13. If 231 cubic inches will hold one gallon of water, approximately how many gallons of water will the solid in #5 hold?
  ::13. 如果231立方英寸能维持1加仑的水,5号楼的固体能维持大约多少加仑的水?

  播放段落

  14. The volume of a cone is   $\begin{array}{r}125\pi i{n}^3\end{array}$ . The height is three times the length of the radius. What is the height of the cone?
  ::14. 锥体体的体积是125 英寸3. 高度是半径的三倍。锥体的高度是多少?

  播放段落

  15. The volume of a pentagonal prism is   $\begin{array}{r}360i{n}^3\end{array}$ . The height of the prism is 3   in . What is the area of the pentagon base?
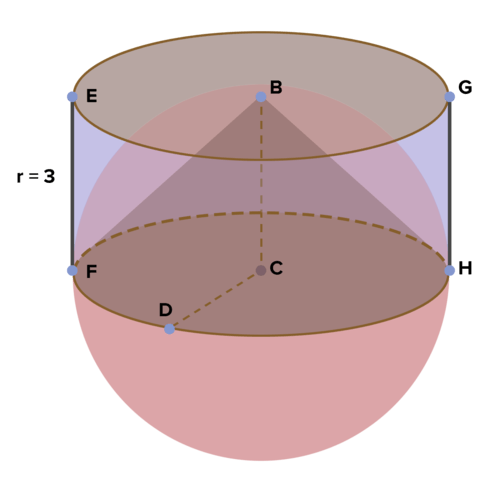
  ::15. 五角形棱镜的体积是360英寸,棱镜的高度是3英寸。五角形基座的面积是多少?

  播放段落

  16. The figure below features a cylinder whose height is 3 units. Inside the cylinder is a hemisphere   (half of a sphere). And inside the hemisphere is a cone. Find the volume of the cylinder and the cone. Find the volume of the sphere and then the hemisphere.  Do you see a relationship between the volume of the cylinder and cone, and that of the hemisphere? Explain. Use this to derive the formula for volume of a sphere from the formulas for a cylinder and cone.
  ::16. 下图显示圆柱体的高度为3个单位,圆柱体的高度为3个单位,圆柱体的高度为一个半球(球体的一半),而半球的高度为一个锥体。找出圆锥体和锥体的体积。找出圆柱体和锥体的体积,然后找到圆锥体的体积。你看到圆柱体和锥体的体积与半球的体积之间的关系吗?请解释。用这个来从圆柱体和锥体的公式中得出球体体体积的公式。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。