2.4 反思-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节反思

  折叠 展开

  反思

  播放段落

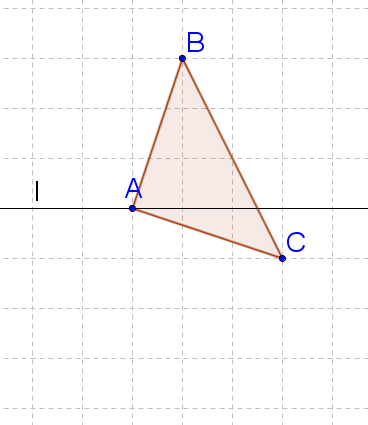
  A reflection is one example of a rigid transformation . A reflection over line is a transformation in which each point of the original figure (the pre-image) has an image that is the same distance from the reflection line as the original point, but is on the opposite side of the line. In a reflection, the image is the same size and shape as the pre-image. A reflection across line $\begin{align*}l\end{align*}$ moves each point $\begin{align*}P\end{align*}$ to $\begin{align*}P^\prime\end{align*}$ such that line $\begin{align*}l\end{align*}$ is the perpendicular bisector of the segment connecting $\begin{align*}P\end{align*}$ and $\begin{align*}P^\prime.\end{align*}$
  ::反射是僵硬转换的一个例子。反射线的反射是原始图象(预图象)的每个点与反射线的距离与原图象的距离相同,但是在反射线的对面。反射图象的大小和形状与预图象的大小和形状相同。反射线的反射线将每个点P移到P,这样一行的反射线I是连接P和P的部段的直角两侧部分。

  播放段落

  In other words, the line segment connecting a point in the pre-image to the matching point in the image is split in half by the mirror line.
  ::换句话说,将图像预视点与图像匹配点连接的线段,由镜像线拆分一半。

  ---

  播放段落

  Reflecting Shapes
  ::反映形状

  播放段落

  Below, the quadrilateral $\begin{align*}ABCD\end{align*}$  (the pre-image) has been reflected across line $\begin{align*}l\end{align*}$ to create a new quadrilateral ,  $\begin{align*}A'B'C'D'\end{align*}$  (the image).
  ::以下四边ABCD(图象前版)被跨线反映,以创建一个新的四边形,A'B'C'D'(图象)。

  播放段落

  Reflections move all points of a shape across a line called the line of reflection  (sometimes informally called the mirror line). A point and its corresponding point in the image are each the same distance from the line.
  ::反射将形状的所有点移动到名为反射线的直线上( 有时非正式地称为反射线 ) 。 图像中的一个点及其相应的点与线的距离相同 。

  播放段落

  Notice that the segments connecting each of the corresponding points are all perpendicular to line $\begin{align*}l\end{align*}$ . Because each point and its corresponding point are the same distance from the line, line $\begin{align*}l\end{align*}$ bisects each of these segments. This is why line $\begin{align*}l\end{align*}$ is called the perpendicular bisector for each of these segments.
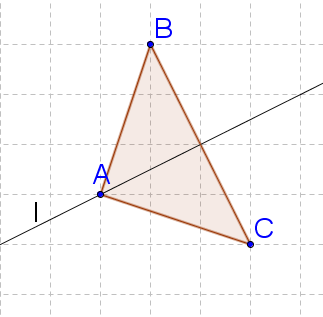
  ::请注意,连接每个相应点的区段都与第1行垂直。由于每个点及其相应点与线段的距离相同,因此,第1行将这些区段的每个区段进行双切。这就是为什么第1行被称为每个区段的垂直分段。

  播放段落

  Keep in mind that you can perform reflections even when the line of reflection is “slanted” or the grid is not visible; however, it is much harder to do by hand.
  ::请注意,即使反射线是“倾斜的”或网格不可见,也可以进行反射;然而,手工反射要难得多。

  

  ---

  播放段落

  Reflection
  ::反射反射

  播放段落

  Select the direction in which you want to reflect the shape. Play with different shapes from triangle up by adding or removing points. Explore the reflection of various shapes by dragging any of the points.
  ::选择要映射形状的方向。从三角形向上,用不同的形状从三角形向上,通过添加或删除点来玩。通过拖曳任意一个点来探索各种形状的反射。

  播放段落

  Horizontal
  ::水平水平水平

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  ---

  播放段落

  Determining the Line of Reflection
  ::确定反射线

  播放段落

  Observe the line of reflection that created the reflected image below.
  ::观察下方反射图像的反射线。

  播放段落

  The fact that point $\begin{align*}D\end{align*}$ is in the same location as point $\begin{align*}D^\prime\end{align*}$ tells you that the line of reflection passes through point $\begin{align*}D\end{align*}$ . Imagine folding the graph so that each point on the original matched its point on the image. Where would the fold be?
  ::D点的位置与 D 点的位置相同,这一事实告诉您反射线穿过 D点。 想象一下将图形折叠, 使原始点的每个点与图像上的点匹配。 折叠点会在哪里?

  播放段落

  The line of reflection is the line $\begin{align*}y=x\end{align*}$ . When reflections are performed on graph paper with axes, you can define the lines of reflections with their equations. $\begin{align*}\ \\ \ \\\end{align*}$
  ::反射线是线 y=x。当反射用轴在图形纸上进行时, 您可以用方程式来定义反射线 。

  ---

  播放段落

  Determining Reflection
  ::确定反射

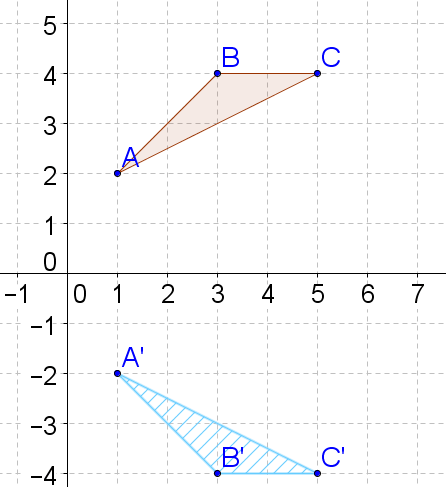
  播放段落

  1. Is the following transformation a reflection?
  ::1. 以下转变是否是一种反思?

  播放段落

  Even though overall both the parallelogram and its image are 2 units from the $\begin{align*}x\end{align*}$ -axis, each individual point is  not the same distance from the $\begin{align*}x\end{align*}$ -axis as its corresponding image.
  ::尽管从总体上看,平行图及其图像都是来自x轴的2个单位,但每个点与X轴的距离与其相应的图像不同。

  播放段落
  • P oint $\begin{align*}A\end{align*}$ is 3 units from the $\begin{align*}x\end{align*}$ -axis and point $\begin{align*}A^\prime\end{align*}$ is 2 units from the $\begin{align*}x\end{align*}$ -axis.
    ::A点是 X 轴的 3 个单位, A 点是 X 轴的 2 个单位。
  播放段落
  • The line of reflection for points $\begin{align*}A\end{align*}$ and $\begin{align*}A^\prime\end{align*}$ would be the line $\begin{align*}y=\tfrac{1}{2},\end{align*}$  which is not the same line of reflection for points $\begin{align*}D\end{align*}$ and $\begin{align*}D^\prime.\end{align*}$
    ::A点和A点的反射线将是y=12线,这与D点和D点的反射线不同。
  播放段落
  • This is not a reflection (it is a translation).
    ::这不是一个反省(它是翻译)。

  播放段落

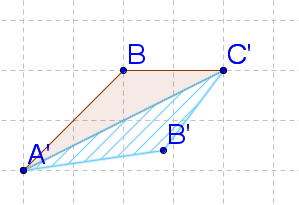
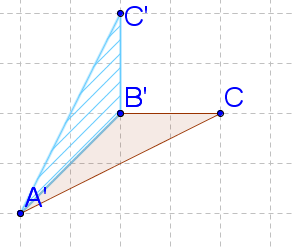
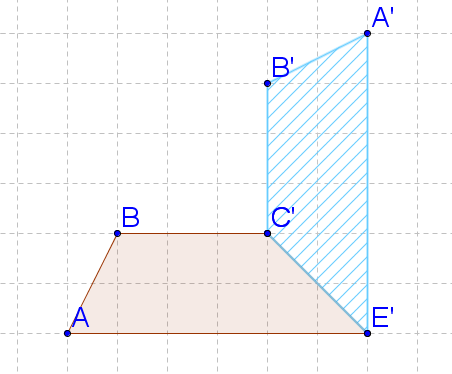
  2. Perform the reflection across line $\begin{align*}l\end{align*}$ .
  ::2. 跨线进行反射。

  播放段落
  • Draw a perpendicular line from each point that defines the parallelogram to line $\begin{align*}l.\end{align*}$
    ::从每个点绘制直角线, 以定义平行图到行 1 。
  播放段落
  • Count the units  between each point and line $\begin{align*}l\end{align*}$ along the perpendicular lines .
    ::沿着垂直线计算每个点和线I之间的单位。
  播放段落
  • Count the same number of units on the other side of line $\begin{align*}l\end{align*}$ along the perpendicular lines to create the image.
    ::沿着垂直线在I线另一侧计算相同的单位数,以创建图像。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Reflections are often informally called "flips". Why is this?
  ::思考通常被非正式地称为“翻转”。为什么这样?

  播放段落

  A reflection is informally called a “flip” because it's as if you are flipping the shape over the line of reflection.
  ::反射被非正式地称为“翻转”, 因为它仿佛正在翻转反射线上的形状。

  播放段落

  Example 2
  ::例2

  播放段落

  Consider the r eflection of a triangle across the $\begin{align*}x\end{align*}$ -axis.
  ::考虑 X 轴上方三角形的反射。

  播放段落

  What do you notice about the coordinates of each point and its image when a reflection is  performed across the $\begin{align*}x\end{align*}$ -axis?
  ::当反射横跨 X 轴进行时, 你注意到每个点的坐标及其图像吗 ?

  

  播放段落

  The $\begin{align*}x\end{align*}$ -coordinate of each point and its image are the same, but the $\begin{align*}y\end{align*}$ -coordinate has changed sign. You could describe this as $\begin{align*}(x, y) \rightarrow (x, \text{-}y).\end{align*}$
  ::每个点的 x 坐标及其图像是相同的, 但 Y 坐标已经更改了符号 。 您可以将此描述为 (x,y)...(x,y)...(x,y) 。

  播放段落

  Example 3
  ::例3

  播放段落

  Describe the line of reflection that created the reflected image below.
  ::描述创建以下反射图像的反射线。

  播放段落

  Connect $\begin{align*}A\end{align*}$ with $\begin{align*}A^\prime.\end{align*}$  This line segment has a slope of -1 and a midpoint at (2, 1).
  ::连接 A 与 A 连接。 该线段的斜度为-1, 中点为(2, 1) 。

  播放段落

  The line of reflection is the perpendicular bisector of this segment. This means it passes through its midpoint and has an opposite reciprocal slope $\begin{align*}\left(-\tfrac{1}{1} \rightarrow +\tfrac{1}{1}\right).\end{align*}$
  ::反射线是这一段的垂直对角,即穿过中点,具有相反的对等斜坡(-1111)。

  播放段落

  The line of reflection is the line
  ::反向线就是反向线

  播放段落

  $$\begin{align*}y - y_1 & = m(x-x_1)\\ y - 1 & = 1 ( x-2) \\ y - 1 & = x - 2 \\ y & = x -1 \\\end{align*}$$
  ::y-y1=m(x-x1)- 1=1(x-2)-y- 1=x-2y=x-2y=x-1

  Summary

  播放段落 A reflection is a rigid transformation where each point of the original figure has an image that is the same distance from the reflection line but on the opposite side of the line. ::反射是一种僵硬的转变,即原始图的每个点的图像与反射线的距离相同,但在反射线的对面。 播放段落 The line of reflection is the line at which all points of a shape are moved across. ::反射线是形状所有点移动的线条。 播放段落 Each point and its corresponding point are the same distance across the line of reflection. ::每个点及其相应的点是反射线之间的相同距离。 播放段落 To determine the line of reflection imagine folding the graph so that each point on the original figure matches its point on the image. ::要确定反射线, 想象一下折叠图形, 使原始图的每个点与图像的点吻合 。 播放段落 To perform a reflection, draw a perpendicular line from each point to the line of reflection, count the units between each point and the line, and count the same number of units on the other side of the line along the perpendicular lines to create the image. ::要进行反射,请绘制从每个点到反射线的垂直线,计算每个点和线之间的单位,并沿着直径线另一侧的单位数目相同,以创建图像。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  Describe the line of reflection that created each of the reflected images below.
  ::描述产生以下每一幅反射图像的反射线。

  1.

  

  2.

  

  3 .

  

  4.

  

  播放段落

  For questions 5 - 8, reflect each shape across line  $\begin{align*}l\end{align*}$ .
  ::对于问题5至问题8,反映横跨一线的每个形状。

  5.

  

  6.

  

  7.

  

  8.

  

  播放段落

  Questions 9 and 10: is the transformation a reflection? Explain.
  ::问题9和问题10:转变是反思吗?解释一下。

  9.

  

  10.

  

  播放段落

  11. Reflect a shape across the   $\begin{align*}y\end{align*}$ -axis. How are the points of the original shape related to the points of the image?
  ::11. 反射Y轴的形状:原始形状的点与图像点的关系如何?

  播放段落

  12. The point (7, 2) is reflected across the   $\begin{align*}y\end{align*}$ -axis. Can you find the coordinates of the image point using the relationship you found in the last question ?
  ::12. 点(7,2)反射到Y轴。您能否使用您在最后一个问题中发现的关系找到图像点的坐标 ?

  播放段落

  13. Reflect a shape across the line   $\begin{align*}y=x\end{align*}$ . How are the points of the original shape related to the points of the image?
  ::13. 反映横跨Y=x线的形状。 原始形状的点与图像点的关系如何?

  播放段落

  14. The point (7, 2) is reflected across the line   $\begin{align*}y=x\end{align*}$ . Can you find the coordinates of the image point using the relationship you found in the last question ?
  ::14. 点(7,2)在y=x线上反射。您能否使用您在最后一个问题中发现的关系找到图像点的坐标 ?

  播放段落

  15. Reflect a shape across the line   $\begin{align*}y=-x\end{align*}$ . How are the points of the original shape related to the points of the image?
  ::15. 反射横线 yx 的形状。 原始形状的点与图像点的关系如何?

  播放段落

  16. The point (7, 2) is reflected across the line   $\begin{align*}y=-x\end{align*}$ . Can you find the coordinates of the image point using the relationship you found in the last question?
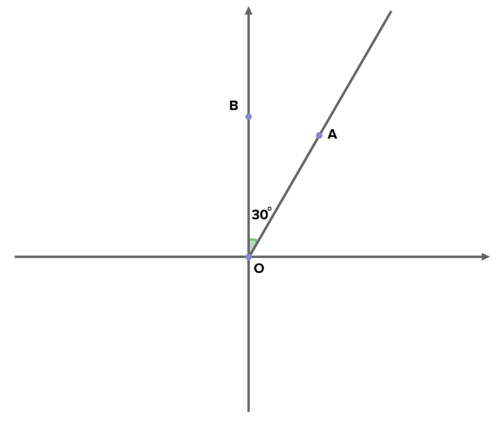
  ::16. 点(7,2)反射到横线yx。您能否使用您在最后一个问题中发现的关系找到图像点的坐标 ?

  播放段落

  17. Given the diagram below, reflect   $\begin{align*}\angle AOB\end{align*}$  across the y-axis and call the resulting image  $\begin{align*}\angle COB\end{align*}$ . What is the measure of  $\begin{align*}\angle COB\end{align*}$ ? What is the measure of  $\begin{align*}\angle COA\end{align*}$ ? Draw sketches to experiment with reflecting angles of different measures and describe your results.
  ::17. 从下图中可以看出,横跨y轴反射 ASOB 并调出生成的图像 QCOB。 QCOB 的量度是多少? QCOA 的量度是多少? 绘制草图以实验反映不同度量角度, 并描述您的结果 。

  

  播放段落

  18. If it hasn't been completed already, perform the reflection described above for  $\begin{align*}m \angle AOB= 45^\circ\end{align*}$ . What is the relationship between  $\begin{align*}\overrightarrow{OC}\end{align*}$  and  $\begin{align*}\overrightarrow{AC}\end{align*}$ ? Explain.
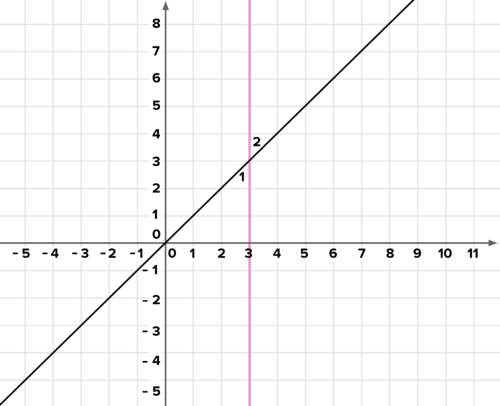
  ::18. 如果尚未完成,请进行上述关于mAOB=45的反思。“OC”和“AC”之间的关系是什么?请解释。

  播放段落

  19. The graph of the line  $\begin{align*}y=x\end{align*}$  is shown below. A vertical line is also shown. What is the measure of  $\begin{align*}\angle 2\end{align*}$ ? How do you know? Reflect the vertical line across the line  $\begin{align*}y=x\end{align*}$ . Describe the image. What is the relationship between the image and the original? Explain. 
  ::19. 以下显示Y=x线的图形。还显示一条垂直线。Q=2的量度是多少?您怎么知道? 反射y=x线的垂直线。描述图像。图像与原始图像之间的关系是什么?解释。

  

  播放段落

  20.   Look at  the image below. The line   $\begin{align*}y=x\end{align*}$  is graphed. What are the coordinates of point A? How do those coordinates relate to the triangle shown? Reflect the triangle shown across the line  $\begin{align*}y=x\end{align*}$ . What are the coordinates of the image of A? How do those coordinates relate to the image triangle? How does this explain the rule for reflecting a point across the line  $\begin{align*}y=x\end{align*}$ ? 
  ::20. 查看下方的图像。Y=x线是图形化的。A点的坐标是什么?这些坐标与显示的三角关系如何?反映显示在y=x线上的三角关系?A图像的坐标是什么?这些坐标与图像三角关系如何?这如何解释反映y=x线对面点的规则?

  

  播放段落

  21. If a line is reflected across a line, is the image always parallel to the original? Why or why not? Is the image ever   parallel to the original? If so, under what conditions? Under what conditions is the image of a line reflected across a line coincident with the original?
  ::21. 如果一条线跨线反射,图象总是与原线平行吗?为什么或为什么没有?图像是否与原线平行?如果是,在什么条件下?在什么条件下,线象在原线上反射?在什么条件下,线线面反射的图象与原线一致?

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。