课程： 3.1 共性的定义-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

共性的定义

What is Congruence?
::什么是共性?

When a figure is transformed with one or more rigid transformations , an image is created that is congruent to the original figure.
::当一个图用一种或多种硬质变形转换时,将生成与原始图象一致的图像。

T wo figures are congruent if a sequence of rigid transformations will carry the first figure to the second figure.
::如果一连串的硬质变换将第一个数字与第二个数字相提并论,两个数字是相同的。

In the picture below, trapezoid $\begin{align*}ABCD\end{align*}$ has been reflected , then rotated , and then translated . All four are congruent to one another.
::在下面的图片中, 插件 ABCD 已被反射, 然后旋转, 然后翻译。所有四个都相容。

Recall that rigid transformations preserve distance and angles . This means that congruent figures will have and corresponding sides that are the same measure and length.
::回顾僵硬的变换保留了距离和角度。这意味着相近的数字将具有和对应的两面,其尺寸和长度相同。

In order to determine if two shapes are congruent:
::为了确定两种形状是否一致:

Carefully describe the sequence of rigid transformations necessary to carry the first figure to the second.
::仔细描述将第一个数字移到第二个数字所需的僵硬变换顺序。

AND/OR
::和/或

Verify that all corresponding pairs of sides and all corresponding pairs of angles are congruent.
::核查所有对应的两边和所有对应的两边角度是否一致。

Determining Congruence
::确定一致性

Recall that rigid transformations preserve angles and side lengths.
::回顾僵硬的变形保留了角度和侧长

If one or more rigid transformations can be applied to a polygon to make it exactly overlay another, then the two polygons are congruent.
::如果可以对多边形应用一个或多个硬质变换,使其完全覆盖另一个多边形,那么这两个多边形是相同的。

Consider the two $\begin{align*}ABCD\end{align*}$ and $\begin{align*}FGHI\end{align*}$ . The two rectangles are congruent if transformations to rectangle $\begin{align*}ABCD\end{align*}$ would produce rectangle $\begin{align*}FGHI.\end{align*}$
::考虑两个ABCD和FGHI。如果转换成矩形 ABCD 会产生矩形 FGHI, 则两个矩形是相似的。

A quick visual estimate suggests that if rectangle $\begin{align*}ABCD\end{align*}$ were rotated $\begin{align*}90^\circ\end{align*}$ counterclockwise about the origin , it would produce rectangle $\begin{align*}FGHI.\end{align*}$
::快速的直观估计表明,如果在源头的矩形ABCD旋转 90 / o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ o/ / / / / / / / / / / / / / / / / / / / o/ / / o/ / o/ / / o/ / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /

To verify this, you can check the coordinates of the points and notice that $\begin{align*}(x, y) \rightarrow (\text{-}y, x)\end{align*}$ for rectangle $\begin{align*}ABCD\end{align*}$ to rectangle $\begin{align*}FGHI\end{align*}$ , so this is in fact a $\begin{align*}90^\circ\end{align*}$ counterclockwise rotation about the origin.
::要验证这一点, 您可以检查点的坐标, 并注意( x,y) {( y, x) 矩形 ABCD 以矩形 FGHI , 所以这实际上是对源值的90 / 对应时钟旋转。

Because a rigid transformation on rectangle $\begin{align*}ABCD\end{align*}$ produces rectangle $\begin{align*}FGHI,\end{align*}$ the two rectangles are congruent .
::因为矩形ABCD上的僵硬变形会产生矩形FGHI, 这两个矩形是相容的。

Another way to verify congruency is to verify that all corresponding angles and corresponding sides are congruent.
::核实一致性的另一种方法是核实所有相应角度和对应方是否一致。

In the above example, notice that:
::在上述例子中,通知:

The slope of each line segment making up the rectangles is either +1 or -1.
::构成矩形的每条线段的斜度是+1或-1。

All adjacent sides have opposite reciprocal slopes and are therefore perpendicular . This means that all angles are $\begin{align*}90^\circ,\end{align*}$ and so all pairs of angles are congruent.
::所有相邻的两边都有对等的斜坡,因此是垂直的。这意味着所有角都是90,所以所有角都是相同的。

To find the length of the line segments, you can use the Pythagorean Theorem (which is the same as the distance formula).
::要找到线段的长度, 您可以使用 Pythagorena 理论( 与距离公式相同 ) 。

$\begin{align*}AD=BC=FI=GH=\sqrt{1^2+1^2}=\sqrt{2}\end{align*}$ , so $\begin{align*}\overline{AD} \cong \overline{FI}\end{align*}$ and $\begin{align*}\overline{BC} \cong \overline{GH}\end{align*}$
::AD=BC=FH=GH=12+12+2 所以是FA和BC=BC=FH=GH=12+12+12=2 所以是FA和BC=BC=BC=GH=GH=12+12+12=2

$\begin{align*}CD=BA=FG=IH=\sqrt{2^2+2^2}=2 \sqrt{2}\end{align*}$ , so $\begin{align*}\overline{CD} \cong \overline{HI}\end{align*}$ and $\begin{align*}\overline{AB} \cong \overline{FG}\end{align*}$
::CD=FG=FGIH222222222,所以你和AAFG

Because all corresponding pairs of sides are congruent and all corresponding pairs of angles are congruent, the rectangles are congruent.
::因为所有对应的两边是相同的, 所有对应的两对角度是相同的, 矩形是相同的。

Drawing Conclusions
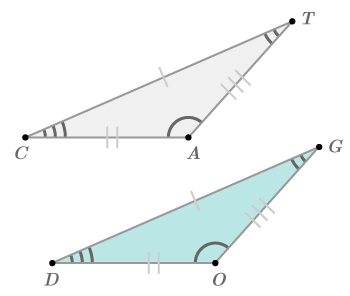
::绘图结论

The triangles below are congruent . What does that tell you about $\begin{align*}\angle B\end{align*}$ and $\begin{align*}\angle C?\end{align*}$
::下面的三角形是相似的。这告诉你什么关于ZB和C?

Because the triangles are congruent, corresponding sides and angles are congruent.
::因为三角形是相容的,对应的边和角度是相容的。

$\begin{align*}\angle A\end{align*}$ corresponds to $\begin{align*}\angle D\end{align*}$ , because both of these angles are in between the sides of lengths 4 and 7, and both are 24 degrees.
::========================================================================== =======================================================================================================================================================================================================================================================================================

$\begin{align*}\angle B\end{align*}$ corresponds to $\begin{align*}\angle E,\end{align*}$ so they have the same measure (since the triangles are congruent).
::B 对应 E, 所以它们具有相同的度量( 因为三角形是相似的) 。

$\begin{align*}\angle C\end{align*}$ corresponds to $\begin{align*}\angle F,\end{align*}$ so they also have the same measure.
::与 F 相对应,所以它们也有相同的措施。

All triangles have angles totaling 180 degrees, and each of these triangles has one angle that is 24 degrees, so
- $\begin{align*}\angle B+\angle C = 180^{\text{o}} - 24^{\text{o}}=156^{\text{o}}\end{align*}$
  ::*BC=180o-24o=156o
- $\begin{align*}\angle E+\angle F = 180^{\text{o}} - 24^{\text{o}}=156^{\text{o}}\end{align*}$
  ::F=180o-24o=156o
::所有三角形的角共共180度, 每个三角形的角均为24度, 所以 BC=180o- 24o=156o EF=180o- 24o=156o

Which other angles total 156 degrees?
::哪个其他角度总共是156度?

Graphing and Translating
::制图和翻译

Graph the square $\begin{align*}S(1, 2), Q(4, 1), R(5, 4)\end{align*}$ and $\begin{align*}E(2, 5)\end{align*}$ .
::图S(1)、2、Q(4)、1、R(5、4)和E(2、5)平方。

Find the image after the translation $\begin{align*}(x, y) \rightarrow (x - 2, y + 3)\end{align*}$ . Then, graph and label the image.
::在翻译 (x,y) {(x- 2,y+3) 后查找图像,然后绘制图像的图和标签。

The indica tes that you should move the square two units to the left, and three units up.
::表示您应该将平方两个单位向左移动,然后将三个单位向上移动。

Examples
::实例实例实例实例

Example 1
::例1

What does congruence have to do with rigid transformations?
::一致性和僵硬的转变有什么关系?

Rigid transformations create congruent figures. You might think of congruent figures as shapes that "look exactly the same," but congruent figures can always be linked to rigid transformations as well. If two figures are congruent, you will always be able to perform a sequence of rigid transformations on one to create the other.
::硬质变换可以创建一致的数字。您可能会把一致的数字视为“ 看上去完全相同 ” 的形状, 但一致的数字也可以总是与僵硬变换相联系。如果两个数字是相同的, 您总是能够对一个进行一系列的僵化变换, 来创造另一个。

Example 2
::例2

Are the two triangles congruent? Explain.
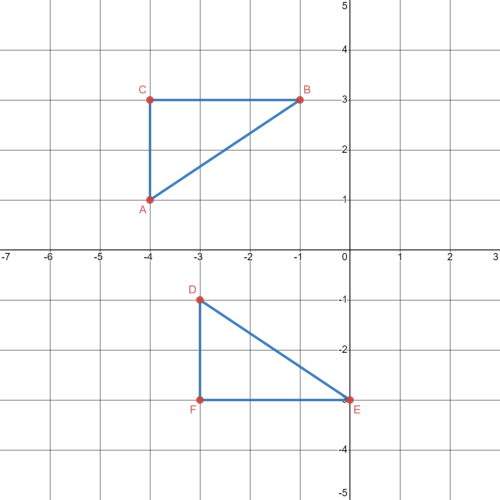
::这两个三角形是否一致?

$\begin{align*}\triangle ABC\end{align*}$ can be reflected across the $\begin{align*}y\end{align*}$ -axis and then translated one unit to the right and four units down to create $\begin{align*}\triangle EFG.\end{align*}$ Therefore, the triangles are congruent .
::ABC 可以在 Y 轴上反射, 然后将一个单位向右翻译, 将四个单位向下翻译, 以创建 Q EFG。因此, 三角形是相容的。

Example 3
::例3

Without using transformations, explain how you know the two triangles below are congruent.
::不使用变换, 请解释您如何知道以下两个三角形是相似的。

The angle measures of $\begin{align*}\angle A \cong \angle F\end{align*}$ , $\begin{align*}\angle C \cong \angle G\end{align*}$ , and $\begin{align*}\angle B \cong \angle E\end{align*}$ , based on the stated measures of each.
::AF、CG和BE的角度量,以各自规定的度量为基础。

$\begin{align*}A\end{align*}$ to $\begin{align*}B\end{align*}$ is 3 units and from $\begin{align*}E\end{align*}$ to $\begin{align*}F\end{align*}$ is 3 units so $\begin{align*}\overline{AB} \cong \overline{EF}\end{align*}$ .
::A到B是3个单位,E到F是3个单位,所以A到B是3个单位。

$\begin{align*}A\end{align*}$ to $\begin{align*}C\end{align*}$ is 4 units and from $\begin{align*}F\end{align*}$ to $\begin{align*}G\end{align*}$ is 4 units so $\begin{align*}\overline{AC} \cong \overline{FG}\end{align*}$ .
::A到C是4个单位 F到G是4个单位所以AC是FG

T he common 3, 4, 5 Pythagorean triple indicates that both $\begin{align*}\overline{BC}\end{align*}$ and $\begin{align*}\overline{EG}\end{align*}$ must be 5 units, so $\begin{align*}\overline{BC} \cong \overline{EG}\end{align*}$ .
- All pairs of corresponding angles and sides are congruent, so the triangles are congruent.
  ::所有对应角度和侧面的对齐都是一致的, 所以三角形是相同的。
::普通的3、4、5比达哥里亚三联表示,BC和BC必须是5个单位,所以BC必须是5个单位。所有相应的角度和两边都是相同的,因此三角形是相同的。

Example 4
::例4

The symbol for congruence is $\begin{align*}\cong\end{align*}$ . $\begin{align*}\triangle ABC \cong \triangle DEF\end{align*}$ means " triangle $\begin{align*}ABC\end{align*}$ is congruent to triangle $\begin{align*}DEF\end{align*}$ ". The order of the letters matters. When you say $\begin{align*}\triangle ABC \cong \triangle DEF\end{align*}$ it means that $\begin{align*}\angle A \cong \angle D\end{align*}$ , $\begin{align*}\angle B \cong \angle E\end{align*}$ , and $\begin{align*}\angle C \cong \angle F\end{align*}$ .
::一致性的符号是。 ABCDEF 意指“ 三角ABC 与三角DEF 相同 ” 。字母的顺序很重要。你说 ABCDEF 意指 AQD, BE 和 CF 。

Suppose $\begin{align*}\triangle CAT \cong \triangle DOG\end{align*}$ . Draw a picture that matches this situation.
::假设是 CATQDOG 。绘制符合这种情况的图片。

Remember that to denote that two sides are congruent, you can either mark them as being the same length (e.g., each 7 units), or use corresponding tick marks. It works the same way with angles. Corresponding angle markings indicate congruent angles.
::记住要指出两面是相同的, 您可以将其标记为相同的长度( 例如每7个单位) , 或者使用相应的刻记。它对角度同样有效。相应的角标记表示相同的角度。

Two triangles labeled with corresponding angles and side markings indicating congruence.

CK-12 PLIX Interactive

::CK-12 PLIX 交互式互动

Summary

Congruence occurs when two figures can be transformed into each other using rigid transformations, such as reflection, rotation, and translation.
::当两个数字可以使用僵硬的变换,如反射、轮换和翻译,相互转换时,就会出现一致性。

Congruent figures have corresponding angles and sides with the same measure and length.
::一致的数字具有相应的角度和侧面,其度量和长度相同。

To determine if two shapes are congruent, describe the sequence of rigid transformations necessary to carry the first figure to the second, and/or verify that all corresponding pairs of sides and angles are congruent.
::为了确定两种形状是否一致,描述将第一个数字移到第二个数字所需的僵硬变换顺序,和/或核实所有对应的两面和角度是否一致。

Review
::审查审查审查审查

Use the triangles below for #1 - #3.
::为 # 1 - # 3 使用下面的三角形。

1. Explain why the triangles are congruent in terms of rigid transformations.
::1. 解释三角形在硬质变换方面为何是一致的。

2. Explain why the triangles are congruent in terms of corresponding angles and sides.
::2. 解释三角形在相应的角度和侧面方面为何一致。

3. Use notation like $\begin{align*}\triangle CAT \cong \triangle DOG\end{align*}$ to state how the triangles are congruent. Note that there are multiple correct ways to write this!
::3. 使用像 QCATDOG 那样的标记来表示三角形是如何相容的。请注意, 写这个字有多种正确的方法 !

Use the parallelograms below for #4 - #6.
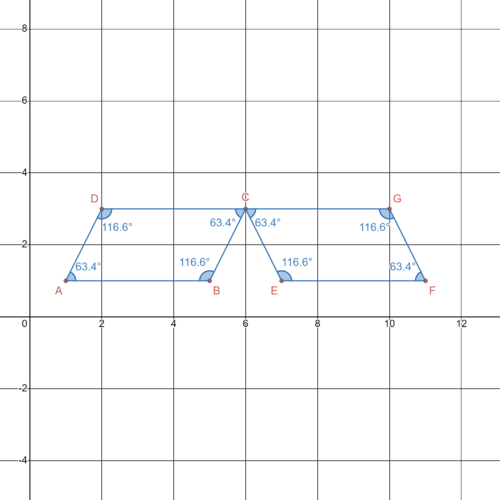
::为 # 4 - # 6 使用下面的平行图示。

4. Explain why the parallelograms are congruent in terms of rigid transformations.
::4. 解释为什么这些平行图在硬质变换方面是相同的。

5. Explain why the parallelograms are congruent in terms of corresponding angles and sides.
::5. 解释为什么平行图在相应的角度和侧面上是一致的。

6. Use notation like $\begin{align*}ABCD \cong A^\prime B^\prime C^\prime D^\prime\end{align*}$ to state how the parallelograms are congruent. Note that there are multiple correct ways to write this!
::6. 使用像 ABCD_A_B_B_C_D_AB_D_ABCD_B_B_C_D_D_D_BBCD_D_D_BBCD_BBCD_B_BB_B_C_D_D_D_D_D_BAR__BCD_BCD_BCD_BCD_BB_BB_B_B_C_D_D_D_D_D_BAR__D_BBCD_BCD_BCD_BCD_BB_B_B_B_B_B_C_D_D_D_D_D_D_D_D_BBAR_D_BCD_BCD_BCD_BCD_BCD_BCD_B_B_B_B_B_B_B_B_B_B_B_B_B_C_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_BBBCD_BCD_BCD_BCD_BB_BCD_BCD_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_B_D_D_B_B_B_B_B_B_B_B_D_B_B_D_D_D_D_D_D_D_D_D_D_D_D_D_D_B_B_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D_D

$\begin{align*}\triangle MRG \cong \triangle KPS\end{align*}$
::MRG KPS(MRG KPS)

7. Draw a picture that matches this situation.
::7. 绘制符合这种情况的图片。

8. $\begin{align*}\angle R \cong \angle \underline{\;\;\;\;\;\;\;\;\;\;}\end{align*}$
::8.

9. $\begin{align*}\overline{RG} \cong \underline{\;\;\;\;\;\;\;\;\;\;}\end{align*}$
::9. RG_RG_

10. $\begin{align*}\overline{SK} \cong \underline{\;\;\;\;\;\;\;\;\;\;}\end{align*}$
::10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个 10个

11. $\begin{align*}m \angle M=60^\circ\end{align*}$ and $\begin{align*}m \angle S=20^\circ\end{align*}$ . What does this tell you about $\begin{align*}m \angle R\end{align*}$ ?
::MM=60和MS=20 这告诉你关于MR的什么?

12. $\begin{align*}\triangle DLP \end{align*}$ is reflected across the $\begin{align*}x\text{-}\end{align*}$ axis, then rotated $\begin{align*}90^\circ\end{align*}$ clockwise to create $\begin{align*}\triangle MRK.\end{align*}$ How are the two triangles related?
::12. QQDLP 分布在 x 轴上,然后按90 时钟旋转以创建 QMRK。这两个三角关系如何?

13. Why will rigid transformations always produce congruent figures? Could non-rigid transformations also produce congruent figures?
::13. 为什么僵化的变迁总是得出一致的数字?非硬化的变迁能否也得出一致的数字?

14. If you know that all pairs of corresponding angles for two triangles are congruent, must the triangles be congruent? Explain and provide a counterexample if relevant.
::14. 如果知道两个三角形的所有对应角度对齐,三角形必须一致吗?如果相关,请解释并提供对应示例。

15. If you know that two pairs of corresponding angles and all pairs of corresponding sides for two triangles are congruent, must the triangles be congruent? Explain and provide a counterexample if relevant.
::15. 如果知道两对对应角度和两个三角形的所有对应边是相同的,三角形必须一致吗?如果相关的话,解释并提供反例。

16. Using the image below, describe a series of rigid motion transformations which map polygon A to A''.
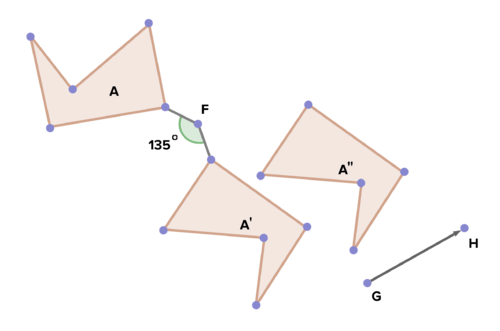
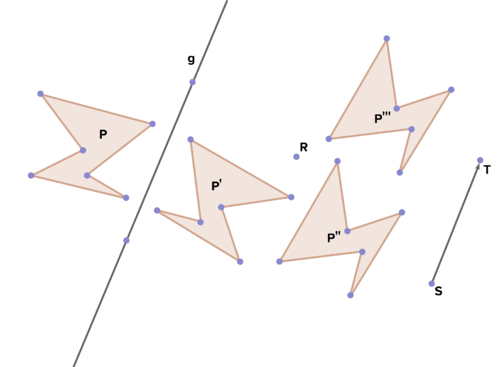
::16. 使用下面的图像,描述一系列绘制多边形A至A'的硬体运动变形。

17. Describe a series of rigid motion transformations which map polygon P to P'''. Is it convincing that P''' is congruent to P? Why or why not? What additional information would one need to know in order to confirm this conclusion?
::17. 描述一系列绘制多边形P到P'的僵硬运动变形。它是否令人信服地认为P'与P是一致的?为什么或为什么不?为了证实这一结论,需要了解哪些补充资料?

18. A figure is rotated around a point, reflected across a line, translated along a vector, then rotated around another point. Is the image congruent to the original? Why or why not?
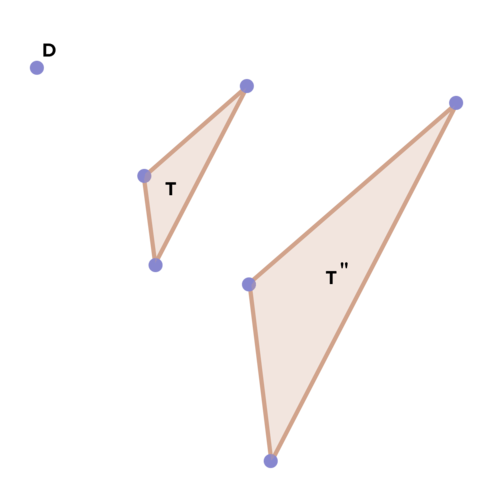
::18. 数字围绕一个点旋转,在一条线上反射,在矢量上翻转,然后在另一点上旋转。图像是否与原始图像一致?为什么或为什么没有?

19. The translation shown below is not a rotation, reflection or translation. Is there a sequence of translations that will map T to its image, T''? Why or why not?
::19. 以下所列翻译不是轮换、反射或翻译,是否有一系列翻译将图示T'T'映射到图象上?为什么或为什么没有?

20. If a polygon undergoes a series of transformations such that the image has the corresponding sides and angles of equal measure to those of the original, can it be said that the original and image are congruent? Why or why not?
::20. 如果一个多边形经历了一系列的变异,使图像具有与原始图像相等的对应面和角度,那么可以说原始图像和图像是相同的吗?为什么或为什么不是?

21. If the image of a polygon after transformation features at least one corresponding length or angle of different measure, can it be said that the image and original are congruent?
::21. 如果变形后多边形的图像至少具有一个相应的长度或不同度量角度,那么可以说图像和原形是相同的吗?

22. Graph a triangle in the coordinate plane such that no sides are vertical or horizontal, and identify the coordinates. Perform a reflection across any given line , and then a translation by any given vector . Be sure to c hoose transformations that that ensure the coordinates of the image can be determined with certainty. Is the image of this sequence of transformations is congruent to the original? Why or why not? Confirm results by using the distance formula to compare the corresponding sides of the image and the original, and by measuring the angles with a compass.
::22. 在坐标平面上绘制三角形图,使无侧面为垂直或水平,并标明坐标。在任何给定的直线上进行反射,然后由给定的矢量进行翻译。一定要选择能够确保图像坐标的变换能够确定。这个变换序列的图像是否与原始变换相一致?为什么或为什么不?通过使用距离公式比较图像对应的侧面和原始的,并通过用罗盘测量角度,确认结果。

23. Graph a right triangle in the coordinate plane such that one leg is vertical. Reflect the triangle across any given line. Be sure to choose a line that ensures the coordinates of the image can be determined with certainty. Is the image of this reflection congruent to the original? Why or why not? Compare corresponding side lengths with the distance formula. How does the slope of the hypotenuse of the image compare with that of the original? Is there a relationship between the slope of the line and the measures of the acute angles?
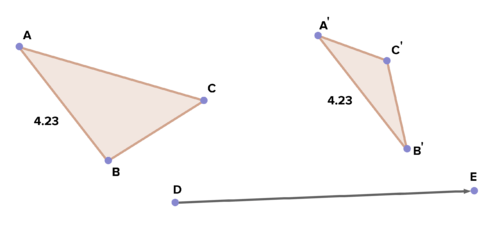
::23. 在坐标平面上绘制一个右三角形,使一个腿垂直。将三角形反射到任何给定的直线上。请确定选择一条确保图像坐标的直线。此反射图像是否与原始相容? 为什么或为什么不? 将相应的侧边长度与距离公式相比较。图像下方斜度与原始平面的斜度如何比较? 线的斜度与急性角的测量值之间是否有关系?

24.Given the triangles the image , is there a rigid motion transformation that will map $\begin{align*}\overline{AB}\end{align*}$ to $\begin{align*}\overline{A'B'}\end{align*}$ ? If so, describe it. Will the same transformation map $\begin{align*}\overline {BC}\end{align*}$ to $\begin{align*} \overline {B'C'}\end{align*}$ ? Why or why not? Are these triangles congruent? Why or why not?
::24. 鉴于三角形的图象,是否有一个僵硬的动作变形,可以绘制“AB”到“A'B”?如果是这样,请描述一下。同样的变形图会是“B'C”还是“B'C”?为什么或为什么没有?这些三角形是否一致?为什么或为什么没有?这些三角形是否一致?为什么或为什么没有?

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

共性的定义

What is Congruence? ::什么是共性?

Determining Congruence ::确定一致性

Drawing Conclusions ::绘图结论

Graphing and Translating ::制图和翻译

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX Interactive ::CK-12 PLIX 交互式互动

Review ::审查审查审查审查

Review (Answers) ::审查(答复)