课程： 3.2 ASA和AAS三角和谐-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

ASA 和 AAS 三角和谐

Identifying Congruent Triangles
::确定相容三角形

If two triangles are congruent it means that all corresponding angle pairs and sides are the same . However, you do not necessarily need to individually verify that all angle pairs and side pairs match exactly to be sure that two triangles are congruent .
::如果两个三角形是相似的,这意味着所有相应的角对和边是相同的。然而,您不一定需要单独核实所有角对和边对是否完全匹配,以确保两个三角形是相同的。

For instance:
::例如:

If you know the measures of two of the three angles in a triangle , there is only one other possible angle, since all three must add up to 180 degrees.
::如果您知道三角形中三个角度中两个角度的度量, 只有一个其他可能的角, 因为所有三个角度加起来必须达到180度。

SO...
::所以... ... So...

If you know that two triangles have two matching angles, then all three angles must be the same . You can see that knowing the right parts of two triangles match is basically the same as knowing that all the parts do.
::如果您知道两个三角形有两个匹配角度, 那么所有三个角度必须是相同的。您可以看到, 了解两个三角形匹配的正确部分基本上和知道所有部分都一样。

But be careful!
::但是要小心!

Two triangles can be exactly the same shape, but different sizes! To be sure the triangles are actually congruent, you also need to know the sides are the same. Fortunately there are shortcuts for that also.
::两个三角形可以是完全相同的形状, 但大小不同。要确定三角形实际上是相似的, 您也需要知道两边是相同的。幸运的是, 也有一些捷径。

Angle-Side-Angle or ASA
::角度- 双角或 ASA

There are a few specific sets of congruent parts of triangles that ensure two triangles are congruent. Each of these 'shortcuts' to proving congruence has an abbreviation that describes the specific parts of the triangles that must be the same to ensure that all corresponding parts are. The abbreviations are meant to be read in order from left-to-right, describing how the parts should relate to each other.
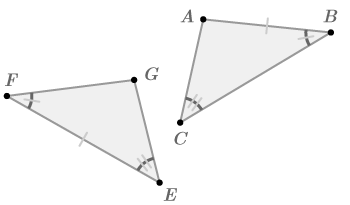
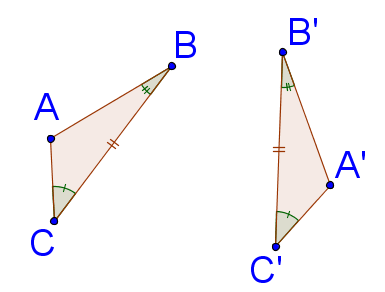
::三角形中有几组特定的一致部分, 以确保两个三角形的一致。每一个用来证明一致的“ 短切点” 都有一个缩略语, 缩略语描述三角形的具体部分, 以确保所有相应的部分都相同。缩略语的意思是按左对右的顺序阅读, 描述这些部分应该如何互相关联。

For example, consider the two triangles in the image :
::例如,在图像中考虑两个三角形:

In these triangles, you can see that there is a matching angle, then a matching side, then another matching angle: $\begin{align*}\angle A \cong \angle D\end{align*}$ , $\begin{align*}\overline{AB} \cong \overline{DE},\end{align*}$ and $\begin{align*}\angle B \cong \angle E.\end{align*}$ In other words, there is a congruent side between two congruent angles . This is commonly referred to as "angle-side-angle" or " ASA ." See how the abbreviation specifies how the congruent parts relate?
::在这些三角形中, 您可以看到一个匹配角度, 然后是匹配边, 然后是另一个匹配角度 : @AD, AB DE 和 {BE 。换句话说, 两个相似角度之间有一个一致的侧面。这通常被称为“ 角边角 ” 或“ ASA ” 。看看缩略语如何指定匹配部分的关联性 ?

The ASA criterion for triangle congruence states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent.
::ASA 三角一致标准规定,如果两个三角有两对相近角度,而一个三角的角的共同侧面与另一个三角的对应侧面相同,则三角是相近的。

ASA works because there is one and only one triangle that can be drawn with specific angle, side, angle information.
::ASA工作是因为只有一个三角形,可以用特定的角、侧、角信息绘制。

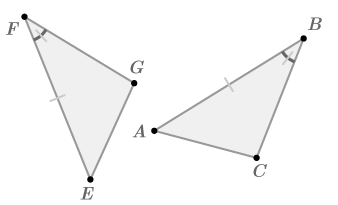
Try it yourself!
::你自己试试看!

Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle $\begin{align*}ABC\end{align*}$ and observe the other triangle $\begin{align*}DEF\end{align*}$ change accordingly to remain congruent.
::单击下方图像旁边的蓝色小箭头,然后拖动橙色的脊椎重塑三角形ABC,并观察其他三角形的DEF相应变化以保持一致。

Try to change either of the grey sides or the grey angle without changing one of the colored parts (the blue and green angles, and the pink/purple side).
::试着改变灰面或灰角, 不要改变有色部分( 蓝色和绿色角度, 粉红/ 粉色) 。

It can't be done! There is only one triangle possible with specific angle-side-angle information .
::无法做到这一点! 只有一个三角形, 可能有特定的角边信息。

Two triangles with congruent angle-side-angle descriptions are congruent across all other parts as well, because there is only one possible triangle with that information.
::两个三角形具有相同的角角角角角形描述,其他各部分的三角形也是一致的,因为该信息只有一个可能的三角形。

ASA Congruence by Rigid Transformation
::ASA 由硬质变换产生的共性

Above, you verified that two triangles must be congruent if they have a congruent side between two congruent angles, because there is only one possible triangle to make with that specific information.
::上面,您验证了两个三角必须一致, 如果两个三角在两个相近角度之间有一个相近的侧面, 因为只有一种三角形可以使用该特定信息进行匹配。

Here you will use rigid transformations to verify ASA in another way. Recall that rigid transformations are called 'rigid' because the figure being transformed is not modified in shape or size at all. In other words, performing rigid transformations on a figure only changes the position or orientation of the figure , not the shape or size.
::在此您将使用硬质变换来用另一种方式验证 ASA 。回顾硬性变换被称为“ 硬性变换 ” , 因为正在变换的数字根本没有形状或大小的改变。换句话说, 在图上进行硬性变换只会改变图的位置或方向, 而不是形状或大小。

Prove that two triangles $\begin{align*}\triangle ABC \text{ and } \triangle DEF\end{align*}$ are congruent, given three things :
::证明两个三角形QABC和QDEF是相容的,有三点:

Angle $\begin{align*}\angle CAB\end{align*}$ is congruent to $\begin{align*}\angle EDF\end{align*}$ (both measure 51 degrees)
::agleCAB 与 EDF 相近(两度为51度)

Side $\begin{align*}\overline{AB}\end{align*}$ is congruent to side $\begin{align*}\overline{ED}\end{align*}$ (both are 7 units long)
::SideAB 与 ED 站在一起是相同的(两个都是7个单元长)

Angle $\begin{align*}\angle ABC\end{align*}$ is congruent to $\begin{align*}\angle FED\end{align*}$ (both measure 45 degrees)
::AgleABC 与 FED 相近( 两度为45度)

Step 1. Perform a rigid transformation to bring point $\begin{align*}D\end{align*}$ to point $\begin{align*}A\end{align*}$ .
::步骤1. 进行僵硬的转变,将D点带入A点。

Draw a vector from point $\begin{align*}D\end{align*}$ to point $\begin{align*}A.\end{align*}$ Translate $\begin{align*}\triangle DEF\end{align*}$ along the vector to create $\begin{align*}\triangle D^\prime E^\prime F^\prime.\end{align*}$
::从 D 点到 A 点绘制矢量。沿矢量绘制一个矢量。 TranslateDEF 以创建 {D\ E_F} 。

Step 2. Measure $\begin{align*}\angle B D^\prime E^\prime\end{align*}$ .
::步骤2. 措施`BD'E。

In this case, $\begin{align*}m \angle BD^\prime E^\prime=84^\circ\end{align*}$ .
::在这种情况下,MBDE84。

Step 3. Rotate $\begin{align*}\triangle D^\prime E^\prime F^\prime\end{align*}$ clockwise that number of degrees about point $\begin{align*}D^\prime\end{align*}$ to create $\begin{align*}\triangle D^{\prime\prime} E^{\prime\prime} F^{\prime\prime}\!.\end{align*}$
::第3步旋转 D E F

Note that because $\begin{align*}\overline{DE} \cong \overline{AB}\end{align*}$ and rigid transformations preserve distance , $\begin{align*}\overline{D^{\prime\prime}E^{\prime\prime}}\end{align*}$ matches up perfectly with $\begin{align*}\overline{AB}.\end{align*}$
::请注意,因为 DE AB 和僵硬的转换保持距离, D E 和AB 完全吻合。

Step 4. Reflect $\begin{align*}\triangle D^{\prime\prime}E^{\prime\prime}F^{\prime\prime}\end{align*}$ across $\begin{align*}\overline{D^{\prime\prime}E^{\prime\prime}}\end{align*}$ (which is the same as $\begin{align*}\overline{AB}\end{align*}$ ).
::第四步,在DE(与AB相同)反射“DEF ” 。

Because $\begin{align*}\angle F^{\prime\prime\prime}D^{\prime\prime\prime}E^{\prime\prime\prime} \cong \angle CAB = 51^{\text{o}}\!,\end{align*}$ and $\begin{align*}\angle F^{\prime\prime\prime}E^{\prime\prime\prime}D^{\prime\prime\prime} \cong \angle CBA = 45^{\text{o}},\end{align*}$ the triangles match up exactly (in particular, $\begin{align*}F^{\prime\prime\prime}\end{align*}$ must map to $\begin{align*}C\end{align*}$ ), and the triangles are congruent.
::因为“F'D'E'CAB=51o”和“F'E'D'CBA=45o”, 三角形完全吻合(尤其是,F'必须绘制地图到C),

This means that even though you didn't know all the side lengths and angle measures, because you knew two pairs of angles and the included sides were congruent, the triangles had to be congruent overall.
::这意味着,即使你不知道所有的侧边长度和角度量, 因为你知道两对角度, 包括的两边是相同的, 三角形必须是相同的整体。

Now you can use the ASA criterion for showing triangles are congruent without having to go through all of these transformations each time, and you can explain why ASA works in terms of the rigid transformations if necessary.
::现在,您可以使用 ASA 标准来显示三角形是相同的, 不必每次经历所有这些变换, 您可以解释为什么 ASA 在必要时在硬质变换方面起作用。

Examples
::实例实例实例实例

Example 1
::例1

The information for the triangles below looks to be angle-angle-side, "AAS". How could you use "ASA" to verify that the triangles are congruent?
::下面三角形的信息看来是角度角形边的“ AAS ” 。您如何使用“ ASA” 来验证三角形是否相容 ?

T he three angles of a triangle always have a sum of $\begin{align*}180^{\text{o}}\!,\end{align*}$ $\begin{align*}m \angle B=56^{\text{o}},\end{align*}$ and $\begin{align*}m \angle E=56^{\text{o}}.\end{align*}$
::三角形的三个角度总有180o、mB=56o和mE=56o之和。

Therefore, the triangles are congruent by ASA due to the fact that $\begin{align*}\angle A \cong \angle D=66^{\text{o}},\end{align*}$ $\begin{align*}\overline{AB} \cong \overline{DE}=6,\end{align*}$ and $\begin{align*}\angle B \cong \angle E=56^{\text{o}}.\end{align*}$
::因此,由于AAD=66o,AB=DE=6,和ZB=56o,这些三角形与ASA是相同的。

This example shows that since ASA is a criterion for triangle congruence, then AAS must also be a criterion for triangle congruence.
::这个例子表明,由于ASA是三角一致性的一个标准,那么AAS也必须是三角一致性的一个标准。

Example 2
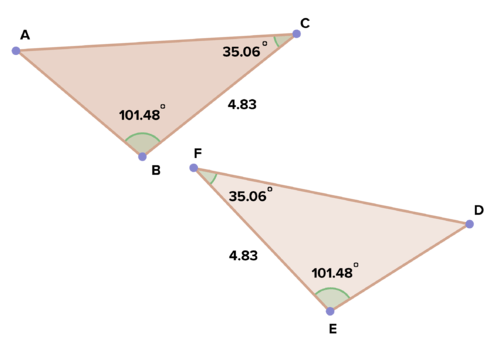
::例2

Are the following triangles congruent? Explain.
::以下三角形是否一致?解释。

The triangles are congruent by ASA.
::三角形与 ASA 相似。

Example 3
::例3

Are the following triangles congruent? Explain.
::以下三角形是否一致?解释。

Two triangles demonstrating congruence through ASA and AAS criteria.

The triangles are not necessarily congruent. The information for $\begin{align*}\triangle ABC\end{align*}$ is AAS while the information for $\begin{align*}\triangle EFG\end{align*}$ is ASA.
::三角不一定一致。 QABC 的信息为 AAS ,而 QEFG 的信息为 ASA 。

Although either ASA or AAS could be used to prove congruence, you are not actually given all three parts of either ASA or AAS for both triangles, so there is not enough information about corresponding sides that are congruent.
::虽然ASA或AAS可以用来证明一致,但对于两个三角,你实际上没有得到ASA或AAS的所有三个部分,因此没有足够关于对应的一致方面的信息。

Example 4
::例4

Are the following triangles congruent? Explain.
::以下三角形是否一致?解释。

What additional information would you need in order to be able to state that the triangles below are congruent?
::您需要哪些补充信息才能声明以下三角形是相同的?

Two triangles are shown, with marked angles and segments for congruence evaluation.

You would need to know that $\begin{align*}\angle G \cong \angle C\end{align*}$ (for AAS), or that $\begin{align*}\angle A \cong \angle E\end{align*}$ (for ASA).
::您需要知道 (AAS) 或 (ASA) 。

Summary

Congruent triangles have all corresponding angle pairs and sides the same, but not all pairs need to be individually verified for congruence.
If two triangles have two matching angles, all three angles must be the same.
::Congruent 三角形的所有对应角度对齐和侧面都相同, 但并非所有对齐都需要单独校验是否一致。如果两个三角形有两个匹配角度, 所有三个角度都必须相同。

Angle-Side-Angle (ASA) criterion states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent.
::角度- 角度- 角度( ASA) 标准指出, 如果两个三角具有两对相容角度, 一个三角的角的正向侧与另一个三角的对角相匹配, 那么三角是相容的。

Angle-Angle-Side (AAS) criterion states that if two triangles have two pairs of congruent angles and the opposite side of the angles in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent.
::角度- 角度- 角度- 角度( AAS) 标准表示, 如果两个三角有两对相近角度, 而一个三角中角的对面与另一个三角中对应的侧面相匹配, 那么三角是相近的。

Review
::审查审查审查审查

1. What does ASA stand for? How is it used?
::1. ASA代表什么?它是如何使用的?

2. What does AAS stand for? How is it used?
::2. AAS代表什么?它是如何使用的?

3. Draw an example of two triangles that must be congruent due to ASA.
::3. 举两个三角形的例子,这两个三角形必须因ASA而相容。

4. Draw an example of two triangles that must be congruent due to AAS.
::4. 举两个三角形的例子,这两个三角形因AAS而必须一致。

For each pair of triangles below, state if they are congruent by ASA, congruent by AAS, or if there is not enough information to determine whether or not they are congruent.
::对于以下每一对三角形,请说明它们是否与ASA一致,与AAS一致,或没有足够的信息来确定它们是否一致。

9. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by AAS? Assume that points $\begin{align*}B\end{align*}$ , $\begin{align*}C\end{align*}$ and $\begin{align*}E\end{align*}$ are collinear.
::9. 为了能够说明以下三角形与AAS相似,你需要哪些最低限度的额外信息?假设B、C和E点为圆线。

10. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by ASA? Assume that points $\begin{align*}B\end{align*}$ , $\begin{align*}C\end{align*}$ and $\begin{align*}E\end{align*}$ are collinear.
::10. 为了能够说明以下三角形与澳大利亚航天局相同,你需要哪些最低限度的额外信息?假设B、C和E点为圆线形。

11. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by AAS?
::11. 为了能够说明以下三角形与AAS相同,你最起码需要哪些补充信息?

12. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by ASA?
::12. 为了能够说明以下三角形与澳大利亚航天局的三角形一致,你需要哪些最低限度的额外信息?

13. If you can show that two triangles are congruent with AAS, can you also show that they are congruent with ASA?
::13. 如果你能证明两个三角形与AAS一致,你也能证明它们与ASA一致吗?

14. Show how the ASA criterion for triangle congruence works: use rigid transformations to help explain why the triangles below are congruent.
::14. 显示三角一致的 ASA 标准是如何运作的:使用硬质变换来解释以下三角为何是相同的。

15. If possible, describe a series of rigid motion transformations that maps $\begin{align*}\triangle ABC\end{align*}$ to $\begin{align*}\triangle DEF\end{align*}$ .
::15. 如有可能,请描述一系列刻板的动作变换,绘制ZQABC至ZDEF的地图。

16. With a partner or on your own, select a side length and two different angles for a triangle such that the third angle will also be different. Without looking at each other's paper (or your prior work), use a ruler and a protractor to sketch the triangle by arranging the sides and angles in two different ways. One person (or your first sketch) should show the selected side length as a side of both selected angles. The second person (or your second sketch) should show the selected side length as a side of only one of the selected angles. Are your triangles congruent or not? Why or why not? What does this tell you about the ASA Triangle Congruence Theorem?
::16. 一个人(或你的第一幅草图)应该将选定的侧边长度作为两个选定角度的侧面。第二个人(或你的第二幅草图)应该将选定的侧面长度显示为所选角度之一的侧面。你的三角形是否相容?为什么不行?这告诉了你什么?

17. If two angles of a triangle are congruent to two angles of another triangle, what must be true about the remaining corresponding angles? Why?
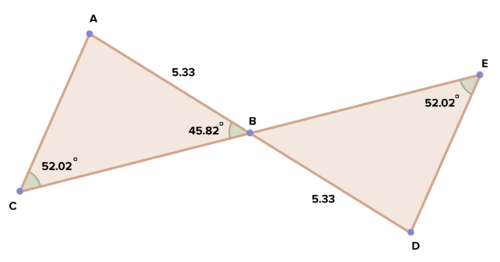
::17. 如果三角形的两个角度与另一个三角形的两个角度相容,那么其余相应角度究竟有什么真实之处? 为什么?

18. Given the diagram below, explain why $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\triangle DBE\end{align*}$ are or are not congruent.
::18. 鉴于下图,请解释为什么ZABC和ZZDBE不一致。

19. Given the diagram below, explain why $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\triangle DBF\end{align*}$ are or are not congruent.
::19. 如下图所示,请解释为什么ZABC和ZZDBF不一致。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

ASA 和 AAS 三角和谐

Identifying Congruent Triangles ::确定相容三角形

Angle-Side-Angle or ASA ::角度- 双角或 ASA

ASA Congruence by Rigid Transformation ::ASA 由硬质变换产生的共性

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::审查审查审查审查

Review (Answers) ::审查(答复)

Identifying Congruent Triangles
::确定相容三角形

Angle-Side-Angle or ASA
::角度- 双角或 ASA

ASA Congruence by Rigid Transformation
::ASA 由硬质变换产生的共性

Examples
::实例实例实例实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::审查审查审查审查

Review (Answers)
::审查(答复)