3.3 SAS三角相互配合-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节SAS 三角和谐

  折叠 展开

  SAS 三角和谐

  播放段落

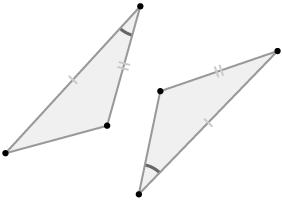
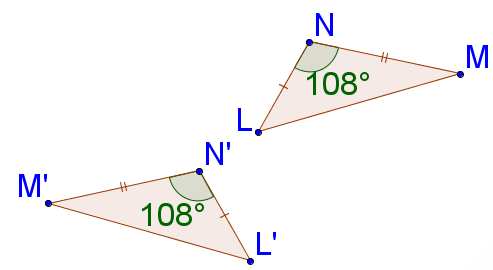
  If two triangles are congruent it means that all corresponding angle pairs and all corresponding sides are congruent. However, in order to be sure that two triangles are congruent, you do not necessarily need to know that all angle pairs and side pairs are congruent. Consider the triangles below.
  ::如果两个三角是相同的,这意味着所有相应的角对和所有对应的边是相同的。然而,为了确保两个三角是相同的,您不必知道所有角对和侧对都是相同的。请看看下面的三角。

  播放段落

  In these triangles, you can see that $\begin{align*}\angle G\cong \angle D\end{align*}$ , $\begin{align*}\overline{IG}\cong\overline{FD}\end{align*}$ and $\begin{align*}\overline{GH}\cong\overline{DE}.\end{align*}$ The information you know about the congruent corresponding parts of these triangles is a s ide, an a ngle, and then another s ide. This is commonly referred to as "side-angle-side" or "SAS".
  ::在这些三角形中, 您可以看到“ GQD ” 、 “ IG ” 、 “FD ” 和“ GH ” 。 您知道的关于这些三角形相匹配的相应部分的信息是侧面、 角度, 然后是另一边。 这通常被称为“ 侧角边 ” 或“ SAS ” 。

  播放段落
  • The criterion for triangle congruence states that if two triangles have two pairs of congruent sides and the included angle (the one between the congruent sides) in one triangle is congruent to the included angle in the other triangle, then the triangles are congruent.
    ::三角一致的标准是,如果两个三角有两对相近的两边,而一个三角中包含的角(相近的两边之间的角)与另一个三角中包含的角一致,那么三角是相同的。

  播放段落

  SAS Triangle Congruence
  ::SAS 三角和谐

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle $\begin{align*}ABC\end{align*}$ and observe the other triangle $\begin{align*}DEF\end{align*}$ changing accordingly to remain congruent.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色的脊椎重塑三角形ABC,并观察其他三角形DEF相应变化以保持一致。

  ---

  播放段落

  In the example, you will use rigid transformations to show why the above SAS triangles must be congruent overall, even though you don't know the lengths of all the sides and the measures of all the angles .
  ::举例来说,你将使用僵硬的变形来显示为什么上述SAS三角形在总体上必须一致,即使你不知道所有方的长度和所有角度的度量。

  播放段落

  SAS by Basic Rigid Transformation
  ::SAS 基本硬变换

  播放段落

  1. Perform a rigid transformation to bring point $\begin{align*}G\end{align*}$ to point $\begin{align*}D\end{align*}$ .
  ::1. 进行僵硬的转变,使G点达到D点。

  播放段落

  Draw a vector from point $\begin{align*}G\end{align*}$ to point $\begin{align*}D\end{align*}$ . Translate $\begin{align*}\triangle GHI\end{align*}$ along the vector to create $\begin{align*}\triangle G^\prime H^\prime I^\prime\end{align*}$ .
  ::从 G 点到 D 点绘制矢量。 沿矢量翻译@GH=GH=I, 以创建 +G$H=I# 。

  播放段落

  2. Measure $\begin{align*}\angle I^\prime DF\end{align*}$ .
  ::2. 措施I`DF。

  播放段落

  In this case, $\begin{align*}m\angle I^\prime DF=148^\circ\end{align*}$ .
  ::在这种情况下,MI'DF=148。

  播放段落

  3. Rotate $\begin{align*}\triangle G^\prime H^\prime I^\prime\end{align*}$ counterclockwise 148 degrees (the measure of $\begin{align*}\angle I’DF\end{align*}$ ) about point $\begin{align*}G^\prime\end{align*}$ to create $\begin{align*}\triangle G^{\prime\prime} H^{\prime\prime} I^{\prime\prime}\end{align*}$ .
  ::3. 逆时针旋转 148 度(I`DF的度量) 约G 点, 以创建 QG H I 。

  播放段落

  Note that because $\begin{align*}\overline{GI}\cong\overline{DF}\end{align*}$ and rigid transformations preserve distance , $\begin{align*}\overline{G^{\prime \prime}I^{\prime \prime}}\end{align*}$ matches up perfectly with $\begin{align*}\overline{DF}\end{align*}$ .
  ::注意,因为GI & DF和僵硬的变换 保持距离,GI"完全匹配的DF'。

  播放段落

  4. Reflect $\begin{align*}\triangle G^{\prime \prime} H^{\prime \prime} I^{\prime \prime}\end{align*}$ across $\begin{align*}\overline {G^{\prime\prime}I^{\prime\prime}}\end{align*}$ (which is the same as $\begin{align*}\overline{DF}\end{align*}$ ).
  ::4. 反射G*H*I* 横跨G*I"(这与FD相同)。

  播放段落

  Because $\begin{align*}\angle EDF\cong \angle{H^{\prime\prime} G^{\prime\prime} I^{\prime\prime}}\end{align*}$ and $\begin{align*}\overline {G^{\prime\prime} H^{\prime\prime}}\cong \overline{DE}\end{align*}$ , the triangles must match up exactly (in particular, $\begin{align*}H^{\prime \prime \prime}\end{align*}$ must map to $\begin{align*}E\end{align*}$ ), and the triangles are congruent.
  ::因为“EDFHGI”和“GHQQDDDDD,三角形必须完全吻合(特别是,H必须绘制地图到E),三角形是相同的。

  播放段落
  • This means that even though you didn't know all the side and angle measures, because you knew two pairs of sides and the included angles were congruent, the triangles had to be congruent overall.
    ::这意味着,即使你不知道所有的侧面和角度量, 因为你知道两对侧, 包括的角度是相同的, 三角形必须是相同的整体。
  播放段落
  • Now you can use the SAS criterion for showing triangles are congruent without having to go through all of these transformations each time, and you can explain why SAS works in terms of the rigid transformations.
    ::现在您可以使用 SAS 标准来显示三角形是相容的, 不必每次经历所有这些变换, 你可以解释为什么SAS 使用硬变换方式。

  ---

  播放段落

  Determining if Two Triangles are Congruent
  ::确定两个三角是否为共字三角

  播放段落

  Is the pair of triangles congruent? If so, write the congruence statement and why.
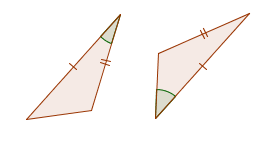
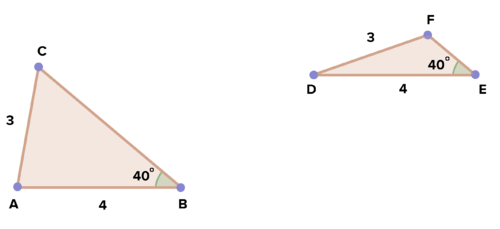
  ::三角形是否一致?如果一致,请写出一致声明和原因。

  播放段落

  While the triangles have two pairs of sides and one pair of angles that are congruent, the angle is not in the same place in both triangles. The first triangle fits with SAS, but the second triangle is SSA. There is not enough information for us to know whether or not these triangles are congruent.
  ::虽然三角形有两对侧面和一对角度,但角在两个三角形中的位置不同。 第一个三角形符合SAS, 但第二个三角形是SSA。没有足够的信息让我们知道这些三角形是否一致。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  When two triangles have two pairs of sides and their included angles congruent, the triangles are congruent. What if the angles aren't included angles?
  ::当两个三角形有两对两对边和它们包括的角相同时,三角形是相同的。如果角度不包括角度呢?

  播放段落

  Even though these triangles have two pairs of sides and one pair of angles that are congruent, the triangles are clearly not congruent .
  ::尽管这些三角形有两对两对侧面和一对角度,但三角形显然并不一致。

  播放段落

  SSA is NOT a criterion for triangle congruence. In order to use two pairs of sides and one pair of angles to show that triangles are congruent, the pair of angles must be included between the pairs of congruent sides.
  ::SSA不是三角一致的标准。 为了使用两对边和一对角来显示三角是一致的,必须把两对角包括在对齐的两对角之间。

  播放段落

  Example 2
  ::例2

  播放段落

  Are the following triangles congruent? Explain.
  ::以下三角形是否一致?解释。

  播放段落

  The triangles are congruent by SAS.
  ::三角形与 SAS 的三角形一致 。

  播放段落

  Example 3
  ::例3

  播放段落

  Are the following triangles congruent? Explain.
  ::以下三角形是否一致?解释。

  

  播放段落

  The triangles are not necessarily congruent. The given angle is not the included angle in both triangles.
  ::三角形不一定一致。给定角度不是两个三角形中包含的角度。

  播放段落

  Example 4
  ::例4

  播放段落

  What additional information would you need in order to be able to state that the triangles below are congruent by SAS?
  ::您需要哪些补充信息才能声明以下三角形与 SAS 一致?

  

  播放段落

  You would need to know that $\begin{align*}\overline{AB}\cong\overline{AD}\end{align*}$ .
  ::你需要知道AB没有。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  Summary

  播放段落 Side-Angle-Side (SAS) criterion states that if two triangles have two pairs of congruent sides and the included angle in one triangle is congruent to the included angle in the other triangle, then the triangles are congruent. ::侧角-侧角-侧角(SAS)标准规定,如果两个三角形有两对相容的两对角,而一个三角形中包括角的角与另一个三角形中包含角的角一致,则三角形是相容的。 播放段落 If a pair of triangles has two pairs of congruent sides and one pair of congruent angles, but the angle is not in the same place in both triangles (SSA), there is not enough information to determine if the triangles are congruent. ::如果一对三角形有两对一致的两面和一对一致的角,但角在两个三角形(SSA)中的位置不同,则没有足够的信息来确定三角形是否一致。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. What does SAS stand for? What does it have to do with congruent triangles?
  ::1. SAS代表什么?它与相容三角有何关系?

  播放段落

  2. What does SSA stand for? What does it have to do with congruent triangles?
  ::2. SSA代表什么?它与相容三角有何关系?

  播放段落

  3. Draw an example of two triangles that must be congruent due to SAS.
  ::3. 举两个三角形的例子,由于SAS,这两个三角形必须一致。

  播放段落

  4. Draw an example of two triangles that are not congruent because all you know is SSA.
  ::4. 举两个三角形为例,两个三角形不相容,因为你们只知道特别服务协定。

  播放段落

  For each pair of triangles below, state if they are congruent by SAS or if there is not enough information to determine whether or not they are congruent.
  ::对于以下每一对三角形,请说明它们是否与SAS一致,或者是否没有足够的信息来确定它们是否一致。

  5.

  

  6.

  

  7.

  

  8.

  

  9.

  

  播放段落

  10. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by SAS? Assume that points $\begin{align*}B\end{align*}$ , $\begin{align*}C\end{align*}$ , and $\begin{align*}E\end{align*}$ are collinear.
  ::10. 为了能够说明以下三角形与SAS相似,你需要哪些最低限度的额外信息?假设B、C和E点为圆线。

  

  播放段落

  11. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by SAS?
  ::11. 为了能够说明以下三角形与SAS相同,你需要哪些最低限度的额外信息?

  

  播放段落

  12. What is the minimum additional information you would need in order to be able to state that the triangles below are congruent by SAS?
  ::12. 为了能够说明以下三角形与SAS相同,你需要哪些最低限度的额外信息?

  

  播放段落

  13. Do you think you always need at least three pairs of congruent sides/angles to show that two triangles are congruent? Explain.
  ::13. 你认为你总是需要至少三对一致的边/角来显示两个三角形是一致的吗?请解释。

  播放段落

  14. If the two pairs of legs are congruent on two right triangles, are the triangles congruent? Explain. Draw a picture to support your reasoning.
  ::14. 如果两双双腿在两个右三角形上吻合,三角形是否吻合?解释。绘制照片支持你的推理。

  播放段落

  15. Show how the SAS criterion for triangle congruence works: use rigid transformations to help explain why the triangles below are congruent.
  ::15. 显示三角一致的SAS标准是如何运作的:使用硬质变换来解释为何以下三角是相同的。

  

  播放段落

  16. Given the diagram below, is there a rigid motion transformation that maps $\begin{align*}\overline{AB}\end{align*}$ to $\begin{align*}\overline{DE}\end{align*}$ ? If so, describe. Is there such a transformation that maps $\begin{align*}\angle ABC\end{align*}$ to $\begin{align*}\angle DEF\end{align*}$ ? If so, is it the same transformation that mapped $\begin{align*}\overline{AB}\end{align*}$ to $\begin{align*}\overline{DE}\end{align*}$ ? Explain. Finally, is there a rigid motion transformation that maps $\begin{align*}\overline{AC}\end{align*}$ to $\begin{align*}\overline{DF}\end{align*}$ ? If so, is it the same transformation as those used for the previous objects? Explain any difference. Can it be concluded that the triangles are congruent? Explain.
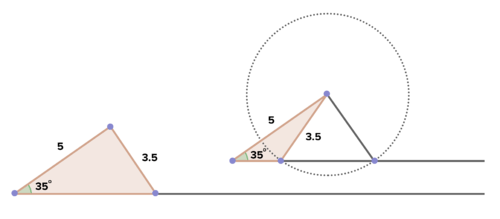
  ::16. 下面的图表显示,是否有一个刻板的动作变换,绘制AB 至 DEF?如果有的话,请描述一下。如果有这样的变换,绘制 ABC 至 DEF ?如果有,那么它是否与绘制AB 至 DEF 的变换相同?解释一下。最后,绘制AC 至 DF 的变换是否是僵硬的变换?如果有,它是否与以前对象的变换相同?解释任何区别。可以断定三角是相同的吗?解释一下。

  

  播放段落

  17. Explain how the diagram below shows that there is not a single rigid motion transformation that maps all the parts of the triangle on the left to the triangle on the right.
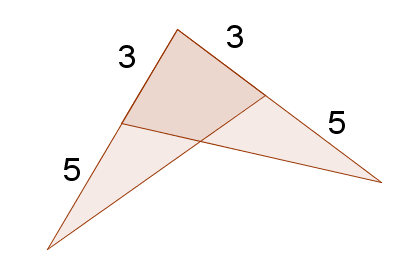
  ::17. 解释下图如何显示没有一个硬动作转换能够将左侧三角形的所有部分映射到右侧三角形。

  

  播放段落

  18. Referring to the side of length 3.5 in the above diagram, is there a length to which this side could be changed that would make it so that the two triangles are congruent? What would be the relationship between this segment and the horizontal ray? Explain.
  ::18. 提到上述图中长度3.5的侧面,是否有一段长度可以改变这一侧,使两边的三角形相容?这一段与水平线之间的关系是什么?请解释。

  播放段落

  Review (Answers) 
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。