4.1 理论和证明-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节理论和证明

  折叠 展开

  理论和证明

  播放段落

  In geometry, a postulate is a statement that is assumed to be true based on basic geometric principles. An example of a postulate is the statement "exactly one line may be drawn through any two points . "  A long time ago, postulates were the ideas that were thought to be so obviously true they did not require a proof.
  ::在几何学中,一个假设是假设基于基本几何原则的正确声明。一个假设的例子就是“一行可以通过任何两个点划出。” 很久以前,假设是那些被认为显然真实的想法,它们不需要证据。

  播放段落

  A theorem is a mathematical statement that can and must be proven to be true. You may have been first exposed to the term when learning about . L earning different theorems and proving they are true is an important part of Geometry.
  ::定理是一个数学语句,它可以而且必须被证明是真实的。在学习 。 学习不同的定理并证明它们的真实性是几何的一个重要部分。

  播放段落

  Theorems and postulates may be more easily understood and applied via conditional statements . Conditional statements are a study in themselves, but as a quick introduction , h ere are a few examples of theorems and postulates written as c onditional statements (also known as if-then statements) :
  ::有条件声明本身就是一项研究,但作为简短的介绍,这里仅举几例作为有条件声明(也称为 " 如果当时的声明 " )书写的理论和假设:

  播放段落
  • Postulate: Through any two points exists one straight line .
    播放段落
    • Conditional statement : If any two points are defined, then exactly one line may be drawn through them both.
      ::有条件说明:如果界定了任何两个点,则可以通过这两个点划出一行。
    
    ::假设: 通过任何两个点存在一条直线。 有条件的语句 : 如果定义了两个点, 则可以通过这两个点划出一条直线 。
  播放段落
  • Postulate: A circle may be drawn with any given radius and center .
    播放段落
    • Conditional statement: If you have a radius and center, then you may draw a circle.
      ::有条件的语句 : 如果您有一个半径和中心, 那么您可以绘制一个圆 。
    
    ::假设 : 一个圆可以与任何给定的半径和中心绘制。 有条件的语句 : 如果您有一个半径和中心, 那么您可以绘制一个圆 。
  播放段落
  • Theorem: Angles that form a linear pair are supplementary .
    播放段落
    • Conditional statement: If two angles form a linear pair, then they are supplementary.
      ::条件说明:如果两个角度形成线性对,则它们是补充性的。
    
    ::理论: 构成线性对的角是补充的。 条件说明: 如果两个角度形成线性对, 那么它们就是补充的 。

  播放段落

  What does it mean to "prove" something? In the past you have often been asked to " justify your answer " or " explain your reasoning. " This is because it is important to be able to show your thinking to others so that ideally they can follow it and agree that you must be right. A proof is just a formal way of justifying your answer. In a proof, your goal is to use given information and facts that everyone agrees are true to show that a new statement must also be true.
  ::何谓“ 证明” ? 过去你经常被要求“ 证明你的回答合理” 或“ 解释你的推理 ” 。 这是因为必须能够向别人展示你的思维, 以便他们最好能遵循, 并同意你必须正确。 证明只是证明你答案的正式方式。 在证据中,你的目标是利用大家同意的信息和事实来证明新声明必须真实。

  播放段落

  Suppose you are given the picture below and asked to prove that $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ . This means that you need to give a convincing mathematical argument as to why the line segments MUST be congruent .
  ::假设您得到了下面的照片, 并被要求证明 AD $ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

  播放段落

  Here is an example of a paragraph-style proof. This is similar to a detailed explanation you might have given in the past.
  ::以下是一段文字式证据的例子,这与你过去可能作出的详细解释类似。

  播放段落

  $\begin{array}{r}\overline{AB}\cong \overline{BC}\end{array}$ because it is marked in the diagram . Also, $\begin{array}{r}\mathrm{\angle }ADB\end{array}$ and $\begin{array}{r}\mathrm{\angle }CDB\end{array}$ are both right angles because it is marked in the diagram. This means that $\begin{array}{r}\mathrm{△}ADB\end{array}$ and $\begin{array}{r}\mathrm{△}CDB\end{array}$ are right triangles because right triangles are triangles with right angles. Both triangles contain segment $\begin{array}{r}\overline{BD}\end{array}$ . $\begin{array}{r}\overline{BD}\cong \overline{BD}\end{array}$ because of the reflexive property that any segment is congruent to itself. $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}CDB\end{array}$ by $\begin{array}{r}HL\cong \end{array}$ because they are right triangles with a pair of congruent legs and congruent hypotenuses. $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ because they are corresponding segments and corresponding parts of must be congruent.
  ::AB {BC\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  There are two key components of any proof -- statements and reasons .
  ::任何证据有两个关键组成部分 -- -- 陈述和理由。

  播放段落
  • The statements are the claims that you are making throughout your proof that lead to what you are ultimately trying to prove is true. Statements are written in blue throughout the previous proof.
    ::声明是您在证明最终证明是真实的的整个证据过程中所做的陈述。 声明在以前的证明中都是以蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。 声明是用蓝色写成的。
  播放段落
  • The reasons are the reasons you give for why the statements must be true. Reasons  generally start with 'because'   in the previous proof. If you don't give reasons, your proof is not convincing and so is not complete.
    ::原因是您给出为什么这些陈述必须是真实的原因。 原因通常以先前的证据中的“ 因为”开头。 如果您不给出理由, 您的证据无法令人信服, 因而不完整 。

  播放段落

  When writing a proof, your job is to make everything as clear as possible, because you need other people to be able to understand and believe your proof. Skipping steps and using complicated words is not helpful!
  ::当写证据时,你的工作就是尽可能地把一切都弄清楚,因为你需要其他人能够理解和相信你的证明。 跳过步骤和使用复杂的词汇是没有帮助的!

  播放段落

  There are many different styles for writing proofs.
  ::写作证明有许多不同的样式 。

  播放段落
  • In American high schools, a style of proof called the two-column proof has traditionally been the most common.

    • 

    
    ::在美国的高中中,一种叫作两栏证明的证明风格历来最为常见。
  播放段落
  • In college and beyond, paragraph proofs like the one above are common.
    ::在大学内外,像上述那样的段落证明是常见的。
  播放段落
  • A style of proof that is more visual is a flow diagram proof .

    • 

    
    ::更直观的证明方式就是流程图证明。

  播放段落

  No matter what style is used, the key components of statements and reasons must be present. You should be familiar with different styles of proof, but ultimately can use whichever style you prefer.
  ::无论使用哪种风格, 语句和理由的关键组成部分都必须存在。 您应该熟悉不同的举证风格, 但最终可以使用您喜欢的样式 。

  播放段落

  Learning to write proofs can be difficult. One of the best ways to learn is to study examples to get a sense for what proofs look like.
  ::学习写证据可能很困难。 学习的最佳方法之一是学习实例,以了解证据的外观。

  ---

  播放段落

  Rewriting Proofs
  ::重写证明

  播放段落

  1.  Restate the proof from the  beginning of the lesson in a two-column format.
  ::1. 以两栏格式从课中开始重写证据。

  播放段落

  Using the picture below, prove that $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ .
  ::用下面的图片来证明AD DDC

  播放段落

  In a two-column proof, the statements and reasons are organized into two columns. All of the same logic that was used in the paragraph proof will be used here. Look at the proof below and compare it to the paragraph proof from the guidance.
  ::在两栏证据中,将说明和理由分为两栏,此处将使用段落证据中使用的所有相同逻辑。看看下面的证据,并将其与指南中的段落证据进行比较。

  Statements	Reasons
  $\begin{array}{r}AB\cong BC\end{array}$	Given
  $\begin{array}{r}\mathrm{\angle }ADB\end{array}$ and $\begin{array}{r}\mathrm{\angle }CDB\end{array}$ are right angles	Given
  $\begin{array}{r}\mathrm{△}ADB\end{array}$ and $\begin{array}{r}\mathrm{△}CDB\end{array}$ are right triangles	Definition of right triangles
  $\begin{array}{r}\overline{BD}\cong \overline{BD}\end{array}$	Reflexive property
  $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}CDB\end{array}$	$\begin{array}{r}HL\cong \end{array}$
  $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$	(corresponding parts of congruent triangles must be congruent)

  播放段落

  There are a couple of points to note about two-column proofs.
  ::有两点需要指出,关于两栏证据。

  播放段落
  1. For a two-column proof, instead of saying "it is marked in the diagram" as a reason, you just write "given". You can use the reason "given" for anything that was stated up front or marked in a diagram. Typically, the first few rows of your proof will always be the "givens".
     ::用两栏证明, 而不是说“ 图表中标记了” 是一个原因, 你只需写“ 设定 ” 。 您可以使用“ 授予 ” 的理由来表示任何在图表中标出或标出的东西。 通常, 您的证据的前几行总是“ 设定 ” 。
  播放段落
  2. In a two-column proof you will use less words than in a paragraph proof, because you are not writing in complete sentences.
     播放段落
     • $\begin{array}{r}HL\cong \end{array}$ and the other criteria for triangle congruence are always acceptable reasons if you have shown in earlier rows that each part of the criteria has been met. You do not need to write a sentence explaining why you can use $\begin{array}{r}HL\cong \end{array}$ .
       ::HL和其他三角一致性标准都是可以接受的理由,如果您在前几行显示每个部分都符合标准。您不需要写句子来解释为什么您可以使用HL。
     播放段落
     • Instead of stating right triangles are triangles with right angles as a reason, you can just say "definition of right triangles". Definitions are always acceptable reasons.
       ::与其说右三角是带有右角度的三角形,倒不如说“右三角形的定义”。定义总是可以接受的理由。
     播放段落
     • CPCTC is an abbreviation for the statement "corresponding parts of congruent triangles are congruent". The abbreviation was developed because this reason is used often, and it can be cumbersome to write it over and over.
       ::CPCTC是“对齐三角形的对应部分是相同的”的缩略语的缩略语。缩略语的写法是因为它经常使用这一理由,而一而再而三地写起来可能很麻烦。
     
     ::在双栏证明中,您将使用比段落证据少的词句,因为您没有以完整句子写字。 HL和三角一致的其他标准总是可以接受的理由,如果您在前面的行中显示每个部分都符合标准。您不需要写一个句子来解释为什么可以使用HL。使用右三角是带有正确角度的三角形,而只是说“对右三角形的定义”而已。定义总是可以接受的理由。 CPCTC是“对齐三角形部分的缩写”的缩写。 缩写是因为经常使用这个理由, 反复写起来可能很麻烦 。

  播放段落

  2. Restate the proof  in a flow diagram format.
  ::2. 以流程图格式重写证明。

  播放段落

  Using the picture below, prove that $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ .
  ::用下面的图片来证明AD DDC

  

  播放段落

  In the flow diagram proof below, statements are written inside and reasons are written below the boxes. In a flow diagram, the statements and reasons  are organized into boxes  and are connected with arrows to show the flow of logic. Look at the proof below and compare it to the two-column and paragraph versions of the same proof.
  ::在下面的流程图证明中,报表在内部写,理由在框下写,在流程图中,报表和理由分为方框,与箭头相连,以显示逻辑流。看看下面的证明,并将其与同一证据的两栏和段落版本进行比较。

  

  播放段落

  There are a couple of points to note about flow diagram proofs.
  ::关于流程图证据,有两点需要注意。

  播放段落
  1. Statements are written inside the boxes and the reasons the statements must be true are written below the boxes.
     ::声明写在方框内,声明必须真实的理由写在方框下。
  播放段落
  2. The arrows show the flow of logic. If two boxes are connected by arrows it means that the statement in the lower box can be made because the statement in the upper box is true. Notice that three boxes point towards the statement that $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}CDB\end{array}$ . This is because all three of those statements were necessary for making the conclusion that the two triangles are congruent.
     ::箭头显示逻辑流。 如果两个框用箭头连接, 这意味着下方框中的语句可以作出, 因为上方框中的语句是真实的。 请注意, 3个框指向 ADBCDB 的语句。 这是因为所有3个语句对于得出两个三角形一致的结论都是必要的 。
  播放段落
  3. Just like in the two-column format, "given" is the reason used for anything that was stated up front or marked in the diagram. The "given" reasons will be towards the top of the flow diagram.
     ::和两栏格式一样,“ 给” 是用于图前方或图中标注的任何东西的理由。 “ 给” 理由将指向流程图的顶部 。
  播放段落
  4. Just like in the two-column format, you use abbreviations where possible. For example:  $\begin{array}{r}HL\cong \end{array}$ , $\begin{array}{r}ASA\cong ,\end{array}$   CPCTC , and definitions are all acceptable reasons.
     ::就像两栏格式一样,尽可能使用缩略语。例如:HL、ASA、CPCTC和定义都是可以接受的理由。

  ---

  播放段落

  Identifying Mistakes
  ::识别错误

  播放段落

  Each proof below has a mistake, can you figure out where the mistake is and why it is a mistake?
  ::下面的每个证据都有错误, 你能找出错误在哪里, 为什么它是一个错误吗?

  播放段落

  Using the picture below, prove that $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ .
  ::用下面的图片来证明AD DDC

  

  播放段落

  PROOF A :
  ::依据A:

  Statements	Reasons
  $\begin{array}{r}\overline{AB}\cong \overline{BC}\end{array}$	Given
  $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}CDB\end{array}$	$\begin{array}{r}HL\cong \end{array}$
  $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$	CPCTC (corresponding parts of congruent triangles must be congruent)

  播放段落

  PROOF B :
  ::B部分: B部分: B部分: B部分: B部分: B部分: B部分:

  播放段落

  $\begin{array}{r}\mathrm{△}ABD\end{array}$ looks to be the same size and shape as $\begin{array}{r}\mathrm{△}CBD\end{array}$ , so the two triangles are congruent . $\begin{array}{r}\overline{AD}\cong \overline{DC}\end{array}$ because they are corresponding segments and corresponding parts of congruent triangles must be congruent.
  ::ABD看起来和CBD的大小和形状相同, 所以两个三角是相同的。 AD {DC} 因为它们是对应的区块, 对应的三角的对应部分必须是相同的 。

  播放段落

  PROOF A is incorrect because it is missing steps. You can't say that the two triangles are congruent by $\begin{array}{r}HL\cong \end{array}$ without having shown that all the parts of the $\begin{array}{r}HL\end{array}$ criteria have been met (congruent leg pair, congruent hypotenuse pair, right triangles). Be careful when writing proofs that you don't skip over steps, even if the steps seem obvious.
  ::PROOF A 不正确, 因为它缺少了步骤 。 您不能说两个三角形与 HLQ 一致, 而没有显示 HL 标准的所有部分都符合 。 ( 相容的腿对、 相近的下垂对、 右三角 ) 。 当写证据证明您不会跳过步骤时要小心, 即使步骤看似明显 。

  播放段落

  PROOF B is incorrect because it did not convincingly explain why the two triangles have to be congruent. Looking congruent is not a good enough reason. For proving triangles are congruent, there are five triangle congruence criteria to use. If you don't have enough information to use one of those five criteria, you can't prove that the triangles are congruent.
  ::PROOF B 不正确, 因为它没有令人信服地解释两个三角为何必须一致。 查看一致并不足以说明理由。 要证明三角是一致的, 需要使用五个三角一致标准。 如果您没有足够的信息来使用这五个标准中的一个, 您无法证明三角是一致的 。

  播放段落

  Remember, your goal when writing a proof is to convince everyone else that what you are trying to show is true actually is true . If you skip steps or use reasons that aren't convincing, other people won't believe your proof. 
  ::记住,你写证据的目的是要让其他人相信,你所要展示的其实是真的。如果你跳过台阶或使用没有说服力的理由,其他人不会相信你的证据。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Most of the geometry concepts and theorems that are taught at the high school level today were first discovered and proved by mathematicians such as Euclid thousands of years ago. Given that these geometry concepts and theorems have been known to be true for thousands of years, why is it important that you learn how to prove them for yourself?
  ::今天在高中教授的几何概念和理论大多是几千年前由欧几里德等数学家首次发现和证明的。 鉴于这些几何概念和理论数千年来一直为人所知,为什么你必须学会如何为自己证明这些概念和理论呢?

  播放段落

  There are many reasons why it is valuable to learn to write proofs for yourself. Even though all of the theorems you will learn in geometry have already been proven, mathematicians today are working on trying to prove new ideas that will hopefully help to advance science/technology/medicine. Writing proofs in geometry class allows you to see what proofs are all about and practice writing them. That way, when you someday want to prove something new, you can feel confident in your proof writing abilities.
  ::学习自己写证据的价值有很多原因。 尽管您在几何学中将学到的所有理论都已经得到证明,但数学家们今天正在努力证明新的想法,希望这些想法能有助于推进科学/技术/医学。 几何学类的写作证明可以使您看到哪些证据,并练习写这些证据。 这样,当你有一天想证明一些新的东西时,你可以对自己的写作能力有信心。

  播放段落

  Writing proofs is all about logic. If you get good at writing proofs, this logical thinking can transfer to other subjects. Writing a persuasive essay about any topic is very similar to writing a paragraph proof. Knowing how to persuade others to believe your way of thinking can be very helpful in many careers and life in general.
  ::写作证明完全与逻辑有关。 如果你擅长写作证明, 这种逻辑思维可以转移到其他科目。 写一篇关于任何主题的有说服力的论文与写一段证明非常相似。 了解如何说服他人相信你的思维方式可以对很多职业和一般生活很有帮助。

  播放段落

  Example 1
  ::例1

  播放段落

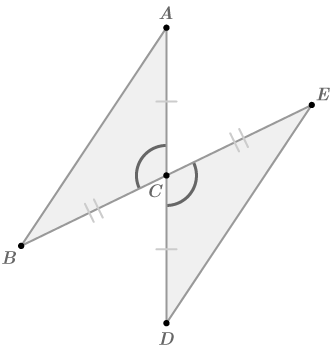
  Given: $\begin{array}{r}C\end{array}$ is the midpoint of $\begin{array}{r}\overline{BE}\end{array}$ and of $\begin{array}{r}\overline{AD}\end{array}$ . $\begin{array}{r}\mathrm{\angle }ACB\cong \mathrm{\angle }DCE\end{array}$ .
  ::C是AD的中点。 'ACB'DCE'。

  播放段落

  Prove: $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$
  ::证明:AB

  播放段落

  No matter which style of proof you use, before starting to write you should brainstorm what you will say in your proof. Start by looking at the given information and thinking about what you know based on each given fact.
  ::无论你使用哪种类型的证据,在开始写作之前,你都应该集思广益地思考你将在证据中说的话。首先从查看给定的信息开始,并根据每个给定的事实来思考你所知道的。

  播放段落
  • The fact that $\begin{array}{r}C\end{array}$ is a midpoint means it is right in the middle of the two line segments. This means there are two pairs of segments that must be congruent. Mark these congruent segments on the diagram as you brainstorm. This will help you to keep track of what you know!
    ::C 是一个中点, 表示它在两个线段的中间。 这意味着有两对相对的区段必须一致。 当您集思广益时, 请在图表中标注这些相对的区段。 这将帮助您跟踪您知道的 !

  播放段落
  • You also are given that $\begin{array}{r}\mathrm{\angle }ACB\cong \mathrm{\angle }DCE\end{array}$ . This should be marked on the diagram as well.
    ::您也可在 QACBDCE 上标注 。 这也应该在图表上标注 。

  

  播放段落

  Next think about what other conclusions you can make based on what you have now marked on the diagram. You have $\begin{array}{r}\cong \end{array}$ criteria marked, so you can say that the two triangles are congruent. This will allow you to be able to say that $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$ , because they are corresponding parts of the triangles.
  ::接下来想想根据您在图表上标记的内容可以得出哪些其他结论。 您已经标记了 {{{{{{{{{{{{{{}} 标准, 这样您就可以说这两个三角是相同的。 这将允许您说 AB {{{{{}}} , 因为它们是三角的对应部分 。

   

  播放段落

  Example 2
  ::例2

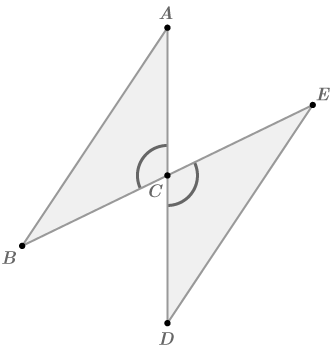
  播放段落

  Write a paragraph proof that shows that $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$ .
  ::写一个段落证据 表明AB 'DE'。

  播放段落

  $\begin{array}{r}C\end{array}$ is the midpoint of $\begin{array}{r}\overline{BE}\end{array}$ and $\begin{array}{r}\overline{AD}\end{array}$ because it is given information . This means that $\begin{array}{r}\overline{AC}\cong \overline{CD}\end{array}$ and $\begin{array}{r}\overline{EC}\cong \overline{CB}\end{array}$ , because midpoints divide segments into two congruent segments. Also, $\begin{array}{r}\mathrm{\angle }ACB\cong \mathrm{\angle }DCE\end{array}$ because it is given information. $\begin{array}{r}\mathrm{△}ACB\cong \mathrm{△}DCE\end{array}$ by $\begin{array}{r}SAS\cong \end{array}$ because they are triangles with two pairs of corresponding sides congruent and included angles congruent. $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$ because they are corresponding segments and corresponding parts of congruent triangles must be congruent.
  ::CIS BE 的中点, 并且因为信息被给出了, 这意味着 AC = CD 和 EC = CB = CB =, 因为中点将部分分割成两个相近的段。 另外, ACB =DCE = 因为它被给出了信息 。 由 SAS = ACB = DCE = ACB = 因为他们是三角形, 对应的两对对对对相近, 包括角度一致 。 AB = = DE = 因为它们是对应的段, 对应的三角形的对应部分必须是相近的 。

  播放段落

  Example 3
  ::例3

  播放段落

  Write a two-column proof that shows that $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$ .
  ::写两栏证据 证明AB=DE

  Statements	Reasons
  $\begin{array}{r}C\end{array}$ is the midpoint of $\begin{array}{r}\overline{BE}\end{array}$ and $\begin{array}{r}\overline{AD}\end{array}$	Given
  $\begin{array}{r}\overline{AC}\cong \overline{CD}\end{array}$ and $\begin{array}{r}\overline{EC}\cong \overline{CB}\end{array}$	Definition of midpoint
  $\begin{array}{r}\mathrm{\angle }ACB\cong \mathrm{\angle }DCE\end{array}$	Given
  $\begin{array}{r}\mathrm{△}ACB\cong \mathrm{△}DCE\end{array}$	$\begin{array}{r}SAS\cong \end{array}$
  $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$	CPCTC

  播放段落

  Example 4
  ::例4

  播放段落

  Write a flow diagram proof that shows that $\begin{array}{r}\overline{AB}\cong \overline{DE}\end{array}$ .
  ::写一个流程图证明 表明AB=DE。

  

  

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  Summary

  播放段落 In geometry, a postulate is a statement that is assumed to be true based on basic geometric principles.  ::在几何学中,假设是一种根据基本几何原则假定属实的声明。 播放段落 A theorem is a mathematical statement that can and must be proven to be true.  ::定理是一种数学说明,可以而且必须证明是真实的。 播放段落 A conditional statement (also called an if-then statement) is a statement with a hypothesis followed by a conclusion.  ::有条件声明(也称为 " 如果当时的声明 " )是附有假设的声明,然后是结论。 播放段落 The statements are the claims that you are making throughout your proof that lead to what you are ultimately trying to prove is true.  ::这些说法就是你们在举证过程中 所说的那些说法 最终证明你所要证明的都是真实的 播放段落 The reasons are the reasons you give for why the statements must be true. Reasons generally start with 'because'. ::原因就在于你为什么这些言论必须真实的原因。 原因通常以“ 因为 ” 开头 。 播放段落 The styles of proofs are two-column proof, paragraph proof, and visual is a flow diagram proof. ::证据的风格是两栏证明,段落证明,视觉是流程图证明。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. What's the difference between a postulate and a theorem?
  ::1. 假设和定理有什么区别?

  播放段落

  2. What are the two main components of any proof?
  ::2. 任何证据的两个主要组成部分是什么?

  播放段落

  3. What does it mean when a reason in a proof is "given"?
  ::3. 当证据的一个理由被 " 赋予 " 时,这意味着什么?

  播放段落

  4. What should the last line/sentence/box for any proof be?
  ::4. 任何证据的最后一行/判决/框应该是什么?

  播放段落

  5. What are three styles of proof?
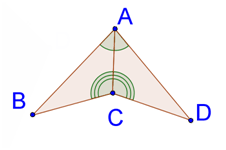
  ::5. 证据的三种形式是什么?

  播放段落

  Use the following image and information to answer 6-8.
  ::使用以下图像和信息回答 6-8 。

  播放段落

  Given triangles $\begin{array}{r}\mathrm{△}ACB\end{array}$ and $\begin{array}{r}\mathrm{△}ACD\end{array}$ as marked, prove that $\begin{array}{r}\overline{AB}\cong \overline{AD}\end{array}$ .
  ::以标记的三角形 ZACB 和 ACD 来证明AB AD 。

  

  播放段落

  6. Fill in the missing statements and reasons in this two-column proof.
  ::6. 填写这一两栏证据中缺失的陈述和理由。

  播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  $\begin{array}{r}???\end{array}$	播放段落 Given ::给
  $\begin{array}{r}\mathrm{\angle }BAC\cong \mathrm{\angle }DAC\end{array}$	播放段落 Given ::给
  $\begin{array}{r}\overline{AC}\cong \overline{AC}\end{array}$	???
  $\begin{array}{r}\mathrm{△}ACB\cong \mathrm{△}ACD\end{array}$	???
  $\begin{array}{r}???\end{array}$	播放段落 CPCTC (corresponding parts of congruent triangles must be congruent) ::CPCCTC(对等三角形的对应部分必须一致)

  播放段落

  7. Rewrite the above proof as a paragraph proof.
  ::7. 将上述证据重写为段落证据。

  播放段落

  8. Rewrite the above proof as a flow diagram proof.
  ::8. 将上述证明重写为流程图证明。

  播放段落

  Use the following image and information to answer 9-11.
  ::使用以下图像和信息回答 9-11 。

  播放段落

  Given the circle with center $\begin{array}{r}G\end{array}$ and  $\begin{array}{r}\mathrm{\angle }HGI\cong \mathrm{\angle }JGK,\end{array}$ prove that $\begin{array}{r}\mathrm{△}HGI\cong \mathrm{△}JGK.\end{array}$
  ::以G和HGIQJGK为核心的圆形 证明是HGIQJGK

  

  播放段落

  9. Fill in the blanks for this paragraph proof:
  ::9. 填写本段证据的空白:

  播放段落

  _______________________ because it is given information. Point $\begin{array}{r}G\end{array}$ is the center of the circle because _______________________. $\begin{array}{r}\overline{HG}\end{array}$ , $\begin{array}{r}\overline{GI}\end{array}$ , $\begin{array}{r}\overline{GJ}\end{array}$ , $\begin{array}{r}\overline{GK}\end{array}$ are all radii of the circle, because they are segments that connect the center of the circle with the circle. $\begin{array}{r}\overline{HG}\cong \overline{GJ}\end{array}$ and $\begin{array}{r}\overline{GI}\cong \overline{GK}\end{array}$ because all ______ are congruent. $\begin{array}{r}\mathrm{△}HGI\cong \mathrm{△}JGK\end{array}$ by _______  because they are triangles with two pairs of corresponding sides congruent and included angles congruent.
  ::G点是圆圈的中心,因為"HG,GJ,GK"是圆圈的半径, 因为它们是连接圆圈中心的部分。"HG"GJ"和GIGK"是因为它们都是相同的。"HGI"JGKby" 因为它们是三角形,有两对对应的对齐, 包括角度一致。

  播放段落

  10. Rewrite the above proof as a two-column proof.
  ::10. 将上述证据重写为两栏证据。

  播放段落

  11. Rewrite the above proof as a flow diagram proof.
  ::11. 将上述证明重写为流程图证明。

  播放段落

  Use the following image and information to answer 12-14.
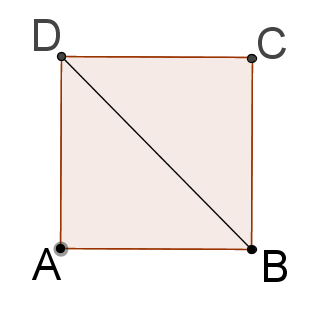
  ::使用以下图像和信息回答 12-14 。

  播放段落

  Given the square  $\begin{array}{r}ABCD,\end{array}$  prove that $\begin{array}{r}\mathrm{△}ABD\cong \mathrm{△}CBD.\end{array}$
  
  ::鉴于正方形ABCD,证明是ABDCBD。

  

  播放段落

  12. Fill in the missing boxes and reasons for this flow diagram proof.
  ::12. 填充缺失的方框和该流程图证明的理由。

  

  播放段落

  13. Rewrite the above proof as a paragraph proof.
  ::13. 将上述证据重写为段落证据。

  播放段落

  14. Rewrite the above proof as a two-column proof.
  ::14. 将上述证据重写为两栏证据。

  播放段落

  15. Give an example of a real life situation where being able to persuade someone else that something is true with a proof.
  ::15. 举一个真实生活状况的例子,即能够说服别人用证据来证明某种事情是真实的。

  播放段落

  16. Before proving something in geometry, one often begins with a conjecture, that is, a prospective idea of something that might be true. For each of the following conjectures, state whether you think the conjecture is true or not. If not, provide a counter-example, that is, an example that shows the statement is false.
  ::16. 在用几何法来证明某事之前,人们往往先从一种推测开始,即预想某事可能属实,对以下每一猜想,都说明你是否认为推测属实,如果不是,则提供反例,即说明声明的事例是假的。

  播放段落
  1. If two rectangles have the same area, their dimensions are the same.
     ::如果两个矩形具有相同的区域,它们的尺寸是相同的。
  播放段落
  2. If two triangles have the same angle measures, their areas are the same.
     ::如果两个三角具有相同的角度度量,则其区域相同。
  播放段落
  3. Any two lines in the same plane which do not intersect are parallel.
     ::同一平面上任何两条不交叉的线是平行的。
  播放段落
  4. If two circles have the same radius, their circumferences are the same.
     ::如果两个圆圈的半径相同,它们的环形相同。
  播放段落
  5. If two circles intersect in two points, they must have radii of different length.
     ::如果两个圆在两点交叉,它们必须具有不同长度的半径。
  播放段落
  6. Two angles that are complementary must be adjacent to each other.
     ::互补的两个角度必须彼此相邻。
  播放段落
  7. Two angles that are vertical must have the same measure.
     ::垂直的两个角度必须具有相同的度量。

  播放段落

  17. Geometry includes definitions, postulates, theorems, and properties. Each of these can be written as conditional statements, that is, if-then statements. For example, the Pythagorean Theorem states that, if a triangle is right with hypotenuse c, then $\begin{array}{r}{a}^2+b^2=c^2\end{array}$ . Rewrite each of the following as conditional statements.
  ::17. 几何包括定义、假设、定理和属性,其中每一种都可以作为有条件的语句,即如果当时的语句来写,例如,Pythagorean 定理称,如果三角形对准下限 c,则a2+b2=c2。以下每一种语句都作为有条件的语句重写。

  播放段落
  1. Supplementary angles sum to $\begin{array}{r}{180}^{\circ }\end{array}$ .
     ::补充角度和180+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  播放段落
  2. Vertical angles have the same measure.
     ::垂直角度具有相同的度量。
  播放段落
  3. All rectangles are parallelograms .
     ::所有矩形都是平行图。
  播放段落
  4. All right triangles have a $\begin{array}{r}{90}^{\circ }\end{array}$  angle.
     ::右三角形有90角角角
  播放段落
  5. In a right triangle, $\begin{array}{r}{a}^2+b^2=c^2\end{array}$ .
     ::在右三角形中, a2+b2=c2。
  播放段落
  6. Opposite sides are parallel in a rhombus.
     ::对面的两面平行在暴风雨中。

  播放段落

  18. There is a big difference between a conditional statement and its converse. The converse of a conditional statement reverses the order. So if the original conditional is if a then b , the converse is if b then a . Sometimes the original conditional will be true and the converse will be false. For example:
  ::18. 有条件声明与其反面之间有很大的区别,条件声明的反面反倒了顺序。因此,如果原始条件是如果a,b,反面是b。有时原始条件是真实的,反面是虚假的。例如:

  播放段落

  If a quadrilateral is a square, then it's a parallelogram. True.
  ::如果四边形是方形,那么就是平行图。

  播放段落

  If a quadrilateral is a parallelogram, then it's a square. False.
  ::如果四边形是一个平行图,那么它就是一个方形。假的。

  播放段落

  In other cases, the original can be false and the converse true, or they can both be true, or they can both be false. Write each of the following as a conditional statement and decide if the statement is true or not. Then write the converse and decide if the converse is true or not.
  ::在其他情况下,原件可能是假的,反之亦然,或两者皆属真实,或两者皆属虚假。 将以下各点写成有条件的声明,并决定声明是否属实。 然后写反之,决定反之是否属实。

  播放段落
  1. The area of a rectangle is given by the formula $\begin{array}{r}\text{Area}=\text{base}\times \text{height}\end{array}$ .
     ::矩形区域由公式“区域”=Basexh8给定。
  播放段落
  2. Lines that intersect at a $\begin{array}{r}{90}^{\circ }\end{array}$ angle are perpendicular.
     ::以 90 角相交的直线是垂直的。
  播放段落
  3. The sum of the interior angles of a triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ .
     ::三角形内部角度的总和是180。
  播放段落
  4. All quadrilaterals are trapezoids.
     ::所有四边形都是类。
  播放段落
  5. Congruent triangles have congruent corresponding angles.
     ::Congruent 三角形具有相似的对应角度 。
  播放段落
  6. A figure has reflection symmetry also has rotation symmetry.
     ::数字的反射对称也有旋转对称。

  播放段落

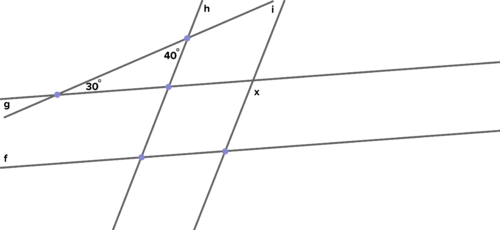
  19. Given $\begin{array}{r}h\parallel i\end{array}$ , and the information in the diagram as shown, find the measure of angle $\begin{array}{r}x.\end{array}$   Add labels to angles as needed, then u se a flow chart, paragraph, or two column proof to explain and justify each step in your solution.
  ::19. 鉴于 hi 和图中显示的信息,找到角度x的度量。 必要时在角度上添加标签,然后使用流程图、段落或两列证明来解释和说明解决方案中每个步骤的理由。

  

  播放段落

  Review (Answers) 
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。