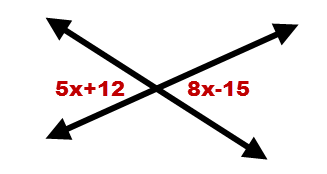4.3 线线和角定理的应用-interactive
Section outline
-
There are four categories of theorems to remember that have to do with lines and angles :
1. When two lines intersect, two pairs of vertical angles are formed.
::1. 当两条线交叉时,形成两对垂直角度。In the diagram above, and are . and are also vertical angles. Vertical angles are always congruent .
::在上图中,%1和%3是.%2和%4也是垂直角度。垂直角度总是一致的。2. When two lines are cut by a transversal , many different angle pairs are formed. If the two lines are parallel , these angle pairs have special properties.
::2. 当两条线被横切切割时,会形成许多不同的角对,如果两条线是平行的,这些角对具有特殊特性。All Angles
::全部角-
and
are
corresponding angles
because their locations are
corresponding
. If lines are parallel, then
are congruent. Other examples of corresponding angles are
and
,
and
, and
and
::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\4\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -
and
are
same side interior angles
because they are inside the lines and on the same side of the
transversal
. If lines are parallel, then
are supplementary. Another example of same side interior angles is
and
::4 和 5 是相同的侧内侧角度, 因为它们位于线内, 并且位于横跨线的同一侧。 如果线是平行的, 那么是补充的 。 相同的侧内侧角度的另一个例子是 3 和 6 。 -
and
are
alternate interior angles
because they are inside the lines and on
opposite
sides of the transversal. If lines are parallel, then
are congruent. Another example of alternate interior angles is
and
::3 和 5 是其它内部角度, 因为它们在横贯线的内侧和对面。 如果线是平行的, 那么是相似的。 另一个替代内部角度的例子就是 4 和 6 。 -
and
are
alternate exterior angles
. If lines are parallel, then
are congruent. Another example of alternate exterior angles is
and
::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\8\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -
and
are
same side exterior angles
. If lines are parallel, then same side
exterior angles
are supplementary. Another example of same side exterior angles is
and
::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
3. The converses of all of the above theorems and postulates are also true and are ways to show that lines are parallel.
::3. 上述所有理论和假设的对立面也是真实的,是显示线条平行的方法。For example, if corresponding angles are congruent then the lines that form them must be parallel. Similarly, if same side interior angles are supplementary then the lines that form them must be parallel.
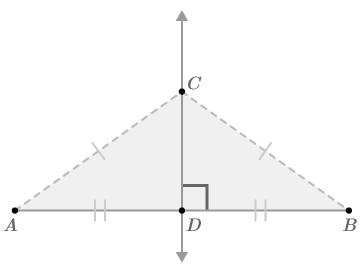
::例如,如果相应的角度是相似的,则构成这些角度的线条必须是平行的。 同样,如果相同的侧侧内角是补充的,则构成这些角度的线条必须是平行的。4. When a line segment is bisected by a perpendicular line , all points on the perpendicular bisector are exactly equidistant from the segment's endpoints (points and in the image below).
::4. 当一条线段被一条垂直线分两部分时,横直线两部分上的所有点与该段端点(下图中的A点和B点)完全相等。For the figure above, as moves along the perpendicular bisector, it will always be true that .
::上图中,C在直角两侧区域移动时,AC ZCB永远是真实的。+Do you want to reset the PLIX?If you remember all of the above postulates and theorems, you can use them to help solve problems.
::如果您记得上面所有的假设和定理, 您可以用它们来帮助解决问题 。
Measuring Angles
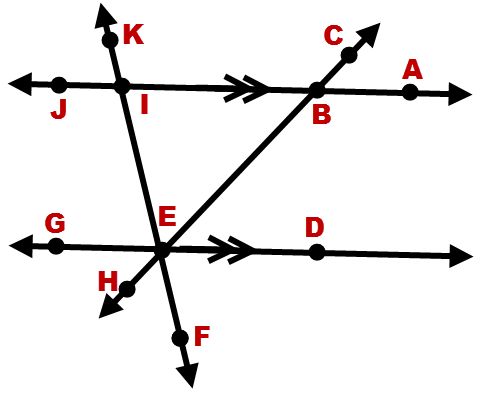
::测量角度If , what is:
::如果MKIB=105,什么是:a.
::a. 公 约-
because it is a
vertical angle
with
and vertical angles are congruent.
::mJIE=105,因为它是一个垂直角度,与 KIB 相近,而垂直角度是相近的。
b.
::b. m DEI-
because it is a
corresponding angle
with
and corresponding angles are congruent when lines are parallel (note that the
markings indicate that the lines are parallel).
::mDEI=105 因为它是一个与 KIB 相对应的角,而当线线平行时对应的角是相同的(注意 > 标记表示线线是平行的)。
c.
::c. m GEI-
because it forms a straight line with
and so those angles are
supplementary
.
::mGEI=75 因为它与 DEI 形成直线, 所以这些角度是补充的 。
+Do you want to reset the PLIX?
Measuring Line Segments
::测量线段Find the length of .
::查找 CB 的长度 。The markings in the picture indicate that is the midpoint of and is a right angle . This means that is the perpendicular bisector of . Therefore, must be equidistant from and , and .
::图片中的标记显示 D 是 AB 的中点, 并且 {CDB 是一个正确角度。 这意味着 CD {} 是 AB 的垂直双形区块。 因此, C 必须与 A 和 B 等距, 和 CB = 2 cm 。
Writing a Proof
::a 写作证明书is shown below. Prove that .
::ABC+CDA 证明这一点。Recall that the definition of a parallelogram is a quadrilateral with two pairs of parallel sides. Since this is a parallelogram, you know that and (Remember that means parallel). With parallel lines comes lots of congruent angles. These angles will help you to show that the triangles are congruent.
::回顾平行图形的定义是一个具有两对平行边的四边形。 由于这是一个平行图, 你知道 AD {BC} 和 AB {DC } (记住 {BC 和 AB {DC 意指平行 ) 。 平行线有很多相似角度。 这些角度会帮助您显示三角形是相似的 。Statements
::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明Reasons
::原因原因原因原因and
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}AB 和AB DC {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}ABDefinition of a parallelogram
::平行图的定义,
::* DACBCA, ACDCABAlternate interior angles are congruent if lines are parallel
::如果线条平行, 替代的内侧角度是相似的Reflexive Property
::弹性财产
::亚塞俄比亚州If you have trouble seeing the alternate interior angles, try extending the lines that form the parallelogram and focusing on one pair of parallel lines at a time.
::如果您无法看到其它的内部角度, 请尝试扩展形成平行图的线条, 并一次关注一对平行线条 。
Examples
::实例实例实例实例Example 1
::例1What can you say about the relationship between and ? What does this have to do with ?
::你能对AB和CD之间的关系说些什么?From the markings in the picture, you can see that and . This means that both and are equidistant from and . Therefore, both and are on the perpendicular bisector of . Therefore, must BE the perpendicular bisector of .
::从照片中的标记中,你可以看到AC {CB}和AD {DB}。这意味着 C和D都与A和B相距相当。因此,C和D都位于AB的垂直两侧区块上。因此,CD必须是AB的垂直两侧区块。Quadrilateral is a because it has two pairs of adjacent congruent sides. The above reasoning shows that one of the diagonals of a kite is the perpendicular bisector of the other diagonal .
::“四边ACBD”是因为它有两对相邻相近的对等面。 以上推理表明风筝的对角是另一对对角的垂直对角。Example 2
::例2In the diagram below, and .
::在下图中, mABC=50 和 mKIJ=80 。1. Find .
::1. 寻找MQEBI。because it is a vertical angle with and vertical angles are congruent.
::mEBI=50 因为它是一个垂直角度 与 ABC 具有相似的垂直角度 。2. Find .
::2. 找到MBIE。because it is a vertical angle with and vertical angles are congruent.
::mBIE=80 因为它是一个垂直角度 与 KIJ 和垂直角度是相似的。3. Find .
::3. 找到MBEI。because , , and form a triangle , and the sum of the measures of the interior angles of a triangle is .
::mBEI=180-(80+50)=50,因为 @EBI、ZBIE和ZBEI组成三角形,三角形内角的测量总和是180+。4. Find .
::4. 寻找MQGEI。because it is a corresponding angle with and corresponding angles are congruent when lines are parallel.
::mGEI=80 因为它是QKIJ的对应角度, 当线条平行时相应的角度是相同的 。+Do you want to reset the PLIX?+Do you want to reset the PLIX?
CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动Summary -
Alternate exterior angles
are two angles that are on the exterior of two parallel lines, but on the opposite sides of the transversal.
::不同的外部角度是两个角度 位于两条平行线的外侧, 而在横向的对面。 -
Corresponding angles
are called that because their locations correspond: they are formed on different lines but in the same position.
::相应的角度被称作, 因为它们的位置相对应: 它们由不同的线条组成, 但位置相同 。 -
Same side interior angles
(sometimes called consecutive interior angles) are on the interior of the figure (between the parallel lines) and on the same side of the transversal.
::同侧内角(有时称为连续内角)位于图的内部(平行线之间)和横向的同一侧。 -
Alternate interior angles
are also on the interior of the figure, but on opposite sides of the transversal.
::其他内部角度也位于图的内侧,但位于横面的对面。 -
For same s
ide exterior angles
(sometimes consecutive exterior angles), if lines are parallel, then same side exterior angles are supplementary.
::对于相同的侧外部角度(有时是连续的外部角度),如果线条平行,则相同的侧外部角度是补充的。
Review
::审查审查审查审查1. Draw an example of vertical angles.
::1. 举一个垂直角度的例子。Use the diagram below for questions 2-4.
::问题2-4使用下图。2. Give an example of same side interior angles. Name each angle with three letters.
::2. 举一个同侧内部角度的例子,用三个字母给每个角度命名。3. Give an example of alternate interior angles. Name each angle with three letters.
::3. 举一个替代内部角度的例子,用三个字母给每个角度命名。4. Give an example of corresponding angles. Name each angle with three letters.
::4. 举一个相应角度的例子,用三个字母给每个角度命名。5. If lines are not parallel, are corresponding angles still congruent?
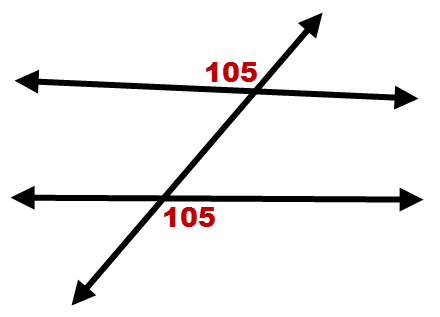
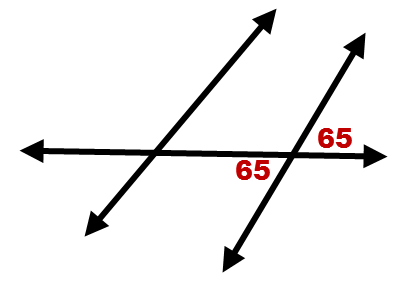
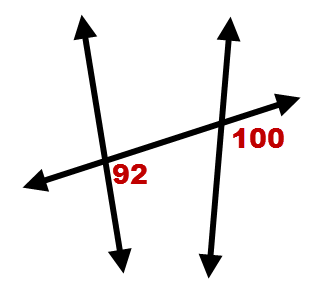
::5. 如果线条不平行,相应的角度是否仍然一致?For 6-9, determine whether or not the lines are parallel based on the given angle measures. Explain your answer in each case.
::对于 6- 9, 根据给定角度计量, 确定线条是否平行。 请解释您在每种情况下的回答 。6.
7.
8.
9.
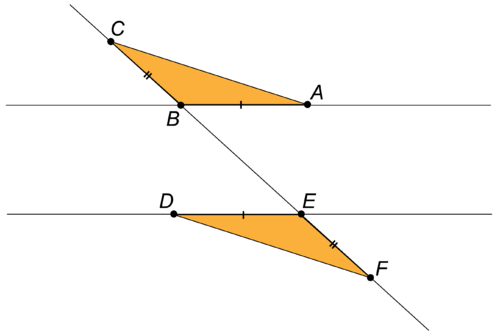
10. In the diagram below, is the midpoint of . Prove that .
::10. 在下图中,C是BD的中点。11. Extend your proof from #10 to prove that .
::11. 将证据从10号延伸至10号 以证明AC CE。12. Which two line segments must be parallel in the picture below?
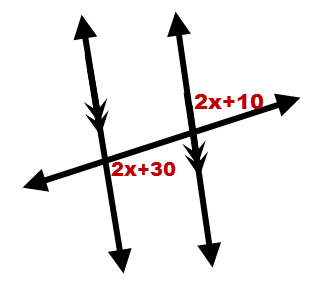
::12. 在下文中,哪些线段必须平行?13. The measures of two angles are given below. Solve for .
::13. 以下列出两个角度的计量。14. The measures of two angles are given below. Solve for .
::14. 以下列出两个角度的计量。15. is the midpoint of and . Find the length of .
::15. D是AB和AC CB的中点。16. Given: ; ;
::16. 鉴于:AB-DE_;AB_DE_;AB_DE_;CB_EF_Prove:
::证明:_BCA_EFD17. Given: ;
::17. 参照:%1 @%2;图表中标注的相近区段Prove:
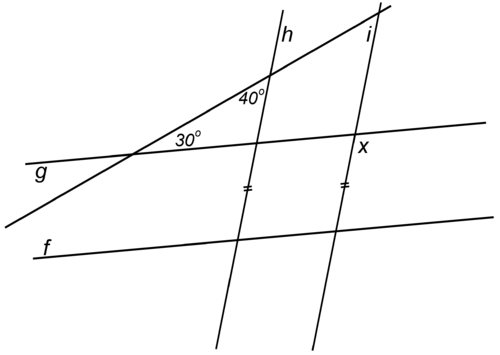
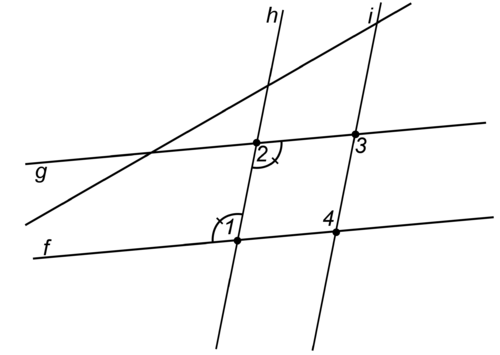
::证明:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________18. Given , f ind in the diagram shown.
::18. 鉴于hi,请在图表中找到x。19. Given:
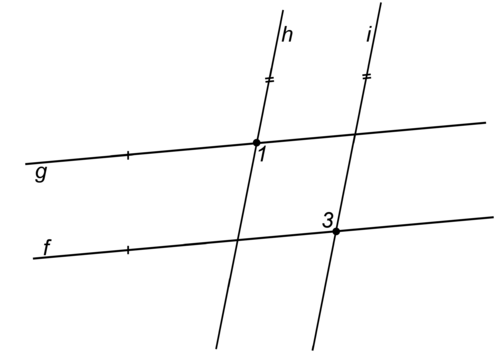
::19. 参照:f_____________________________________________________________________________________Prove: and are supplementary
::证明:%1和%3是补充的20. Given: ;
::20. 参照:f___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Prove: and are congruent
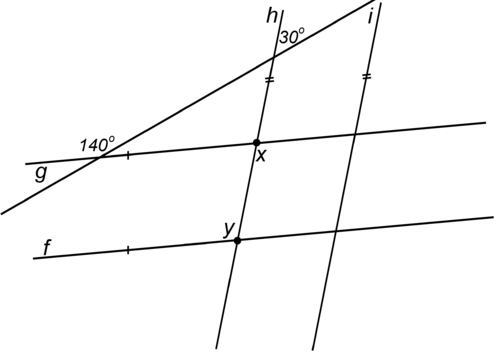
::证明:% 1 和% 3 相同21. Given , find and in the diagram below.
::21. 根据fg,在下图中找到x和y。22. Given:
::22. 鉴于:%1%2Prove:
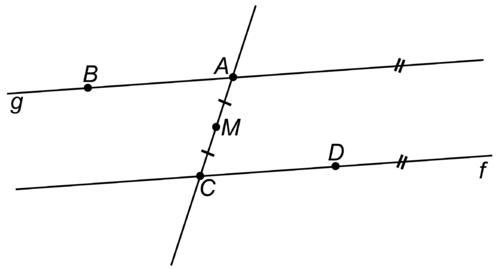
::证明:23. Given: and is the midpoint of . Describe a rigid motion transformation that maps to .
::23. 鉴于:gf和M是AC的中点。描述一个刻板的动作转换,将 BAM 映射为 DCM 。Review (Answers)
::审查(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
and
are
corresponding angles
because their locations are
corresponding
. If lines are parallel, then
are congruent. Other examples of corresponding angles are
and
,
and
, and
and