4.8 四方理论的应用-interactive
章节大纲
-
M any properties of special quadrilaterals can be proved from the specific definitions of the quadrilaterals.
::从四边形的具体定义中可以证明特殊四边形的许多特性。Below is a summary of quadrilateral definitions and properties .
::以下是四边定义和属性摘要。
Parallelogram
::平行图A quadrilateral with two pairs of parallel sides.
::一个四边形,两对平行面-
Parallelogram Theorem #1
: Each
diagonal
of a
divides the parallelogram into two
congruent
triangles.
::平行图定理# # 1: 每个对角将平行图分为两个相似的三角形。 -
Parallelogram
Theorem
#1 Converse: If each of the
diagonals
of a quadrilateral divide the quadrilateral into two congruent triangles, then the quadrilateral is a parallelogram.
::平行图定理# 1 反面 : 如果四边形的对角将四边形分为两个相似的三角形, 那么四边形就是一个平行图。 -
Parallelogram Theorem #2
: The
opposite
sides of a parallelogram are congruent.
::平行图定理 # 2 : 平行图的对面是相似的 。 -
Parallelogram Theorem #2 Converse: If the opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
::平行图定理#2 反面:如果四边形的对面是相似的,那么四边形是平行图。 -
Parallelogram Theorem #3
: The opposite
angles
of a parallelogram are congruent.
::3号平行图定理:平行图的相反角度是相同的。 -
Parallelogram Theorem #3 Converse: If the opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
::3 反面:如果四边形的相反角度是相似的,那么四边形是平行的。 -
Parallelogram Theorem #4
: The diagonals of a parallelogram bisect each other.
::平行图定理4: 平行图双形的对角。 -
Parallelogram Theorem #4 Converse: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
::平行图定理 # 4 : 如果四边形的对角相对, 则四边形是平行图。
Rectangle
::矩形A quadrilateral with four right angles.
::一个四边形,有四个右角度-
Rectangle Theorem #1
: A
rectangle
is a parallelogram.
::矩形定理 # 1 : 矩形是平行图。 -
Rectangle Theorem #2
: A rectangle has congruent diagonals.
::矩形定理 #2: 矩形具有相似的对数法。 -
Rectangle Theorem #2 Converse: If a parallelogram has congruent diagonals, then it is a rectangle.
::矩形定理 # 2 反面 : 如果平行图具有相似的对角线, 那么它是一个矩形 。
Rhombus
::滚轮A quadrilateral with four congruent sides.
::一个四边形 四个对齐面-
Rhombus Theorem #1
: A
rhombus
is a parallelogram.
::Rhombus Theorem # 1 : 暴风车是一个平行图。 -
Rhombus Theorem #2
: The diagonals of a rhombus are
perpendicular
.
::Rhombus Theorem # 2: 伦布鲁斯的对角是垂直的。 -
Rhombus Theorem #3
: The diagonals of a rhombus bisect its angles.
::Rhombus Theorem # 3: 龙卷风的对角线,
Square : A quadrilateral with four right angles and four congruent sides.
::方形:四边形,有四个右角和四个相近的两面。
Kite
::Kite 键A quadrilateral with two pairs of adjacent, congruent sides.
::一个四边形,有两对相邻、相近的两面。-
Kite Theorem #1
: One diagonal of a
bisects the other diagonal.
::Kite Theorem #1:一个对角线,一个对角线,一个对角线,一个对角线,一个对角线,另一个对角线。 -
Kite Theorem #2
: The diagonals of a kite are perpendicular.
::Kite Theorem # 2 : 风筝的对角是垂直的 。 -
Kite Theorem #3
: One diagonal of a kite bisects its angles.
::Kite Theorem # 3: 风筝两角的一个对角, -
Kite Theorem #4
: A kite has one pair of opposite angles congruent.
::Kite Theorem # 4: 风筝有一对相反角度的对齐。
Investigate Kites and Rhombi
::调查Kites和Rhombi
Finding the Perimeter
::寻找周边Find the perimeter of the quadrilateral below.
::在下面找到四边形的周界The markings indicate that the quadrilateral has four congruent sides . This means that the quadrilateral is a rhombus. One property of a rhombus is that its diagonals are perpendicular . This means that the four inner triangles are actually right triangles . You can use to find the hypotenuse of one of these triangles, which will be the length of each side of the rhombus.
::标记显示,四边形有四个相近面。 这意味着四边形是圆柱形。 圆柱形的一个属性是其对角形是垂直的。 这意味着四个内三角形实际上是右三角形。 您可以找到这些三角形中的一个, 也就是圆柱形两侧的长度。
::32+42=c29+16=c25=cSince each side of the rhombus is 5 units long, the perimeter of the rhombus is units.
::由于暴风车的两侧各有5个长,因此暴风车的周边是P=54=20个。
Making and Proving Conjectures
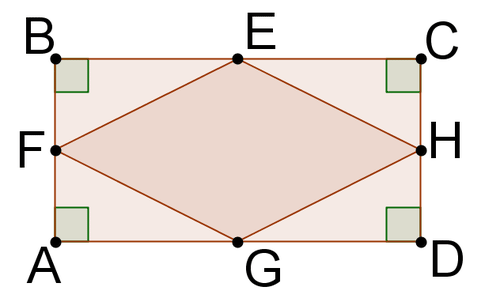
::预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测 预测The midpoints of each of the sides of parallelogram have been connected, as shown below. Make a conjecture about the inner quadrilateral that has been formed. Then, prove the conjecture.
::平行图形 ABCD 的两侧的中点已经连接, 如下文所示。 对已经形成的内四边进行猜测。 然后, 证明这一猜测 。The inner quadrilateral looks to be a parallelogram. To prove it is a parallelogram, prove that its opposite sides are congruent. (Parallelogram Theorem #2 Converse states that if the opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.)
::内四边形看起来是一个平行图。 要证明它是一个平行图, 请证明它的对面是相似的 。 ( Parallelect Theorem # 2 相形之下说, 如果四边形的对面是相似的, 那么四边形是平行图 。 )Given: Parallelogram with midpoints , , , .
::中点为E、F、H、G的平行ABCDProve: is a parallelogram
::证明:EFHG是一个平行图Here is paragraph proof:
::此处为防排段落 :Because is a parallelogram , its opposite sides and angles are congruent. This means that , , , and . , , and are midpoints , so they divide each segment into two congruent segments. Because opposite sides of are congruent, it must be true that , , , and . Therefore, and by . This means that corresponding parts of these triangles are congruent and therefore and . Because opposite sides of are congruent, is a parallelogram .
::因为ABCD是一个平行图, 其对面和角度是相近的。 这意味着 C A, B D, AB DC, 和 AD B B 。 E, F, G 和 H 是中点 。 因此, 它们将每个段分为两个相近的段。 由于ABCD 的对面是相近的, AE CH , 和 ED B 。 因此, AEFCHG 和 BH DG 由 SAS 组成。 这意味着这些三角的对应部分是相近的, 因此 EFG 和 FH G。 因为 EFHG 的对面是相近的, EFHG 是一个平行的图表 。
Naming Shapes
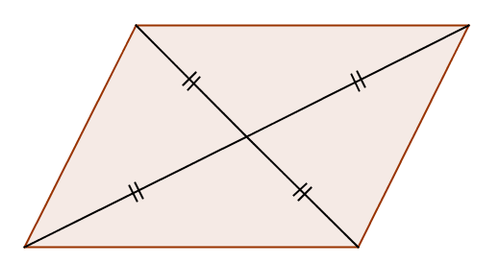
::命名形状Name the shape below based on its markings as precisely as you can. Don't assume that the shape is drawn to scale.
::尽可能精确地根据形状的标记命名下面的形状。 不要假设形状是被画成比例的 。All that is marked is that the shape has four congruent sides. This is the definition of a rhombus so it must be a rhombus. Note that even though it might look like a square , if you don't know for sure that the shape has right angles, you cannot be sure it is a square.
::标记的只是形状有四个相容的面。 这是一个 rhombus 的定义, 所以它必须是一个 rhombus 。 请注意, 即使它看起来像一个正方形, 如果您不确定形状有正确的角度, 您也不能确定它是一个正方形 。
Examples
::实例实例实例实例Example 1
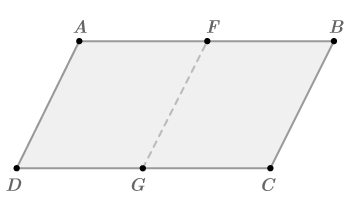
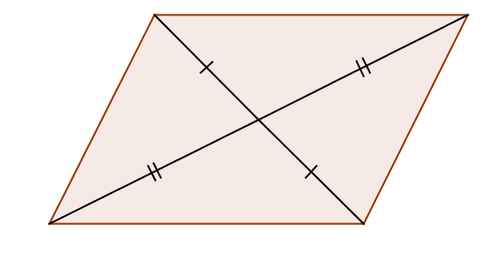
::例1Consider parallelogram below. is the midpoint of and is the midpoint of . Make at least one conjecture about how is related to .
::F是AB的中点,G是DC的中点。至少猜测一下FG与AD的关系。Two possible conjectures are:
::两种可能的假设是:-
::FG 自动 -
::FG 发声
Example 2
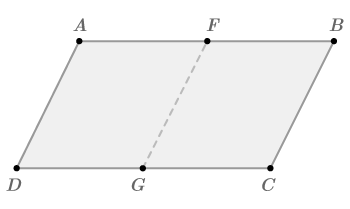
::例2In parallelogram , is the midpoint of and is the midpoint of . Prove that .
::F是AB的中点,G是DC的中点。Draw in . Prove that the two triangles formed are congruent, and therefore corresponding parts (the desired sides) are congruent.
::绘制在 AG 中。 证明形成的两个三角形是相近的, 因此相应的部分( 期望的侧面) 是相匹配的 。Statements Reasons Parallelogram with midpoints and Given , Opposite sides of a parallelogram are congruent and parallel , Definition of midpoint Half of congruent segments are congruent Reflexive Property If lines are parallel then are congruent Example 3
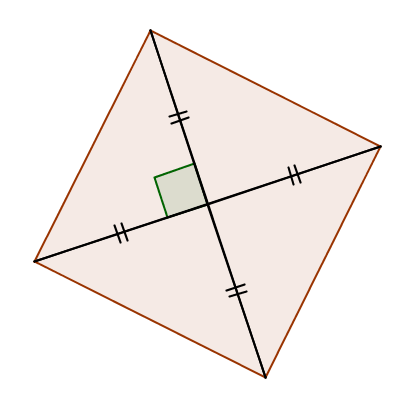
::例3Name the shape below based on its markings as precisely as you can. Don't assume that the shape is drawn to scale.
::尽可能精确地根据形状的标记命名下面的形状。 不要假设形状是被画成比例的 。It is marked that the diagonals are perpendicular. Shapes with perpendicular diagonals are rhombuses, , and squares. Without additional information, you cannot say whether this is a rhombus, a kite, or a square. Therefore, all you can say for certain is that this shape is a quadrilateral.
::标记二角形是垂直的。 具有垂直对角形的形状是正方形, 和正方形。 没有其他信息, 您不能说它是圆柱形、 风筝还是正方形。 因此, 您只能说这个形状是四边形 。Example 4
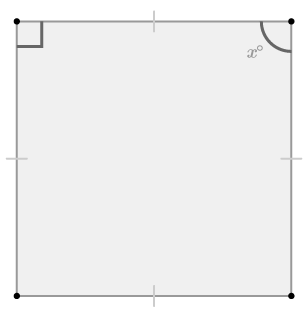
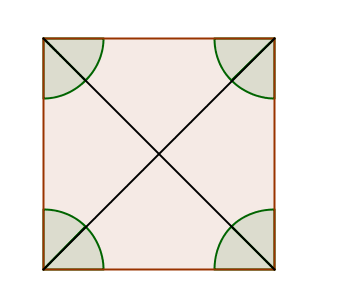
::例4Use the markings on the shape to name the shape. Then, solve for .
::使用形状上的标记来命名形状。 然后, 解析 x 。The shape has four congruent sides which makes it a rhombus. It also has one right angle . Opposite sides of a rhombus are parallel, so are supplementary. This means that . Because opposite angles of a rhombus are congruent, all four angles must be right angles. Therefore, a more precise name for this shape is a square.
::形状有四个相容的边, 使它成为圆柱形。 它也有一个右角。 圆柱形的对面面是平行的, 也是补充的。 这意味着 x=90。 因为圆柱形的对角是相近的, 所有四个角度必须是正角。 因此, 这个形状的更精确的名称是正方形 。
CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动Summary -
A
parallelogram
is a quadrilateral with two pairs of parallel sides.
-
Each diagonal of a parallelogram divides the parallelogram into two congruent triangles.
::每个平行方形的对角将平行方形分为两个相似的三角形。 -
The opposite sides of a parallelogram are congruent.
::平行图的对面是相同的。 -
The opposite angles of a parallelogram are congruent.
::平行图的相反角度是相同的。 -
The diagonals of a parallelogram bisect each other.
::平行相形对齐的对角线
::平行图是一个四边形, 有两对平行边。 平行图的对角将平行图分为两个相似的三角形。 平行图的对角是相似的。 平行图的对角是相似的。 平行图的对角是相似的。 平行图的对角是相似的。 平行图的对角是双形的对角。 -
Each diagonal of a parallelogram divides the parallelogram into two congruent triangles.
-
A
rectangle
is a quadrilateral with four right angles.
-
A rectangle is a parallelogram.
::矩形是一个平行图。 -
A rectangle has congruent diagonals.
::矩形具有相容的对角学。
::矩形是四个右角度的四边形。矩形是平行图。矩形具有相同的对角形。 -
A rectangle is a parallelogram.
-
A
rhombus
is a quadrilateral with four congruent sides.
-
A rhombus is a parallelogram.
::暴风车是平行图。 -
The diagonals of a rhombus are perpendicular.
::暴龙的对角是垂直的。 -
The diagonals of a rhombus bisect its angles.
::龙卷风的对角线 将它的角度分成两部分
::圆柱是一个四边形的四边形。 圆柱形是一个平行图。 圆柱形的对角是垂直的。 圆柱形的对角是两面的对角。 圆柱形的对角是其角度的对角。 -
A rhombus is a parallelogram.
-
A
kite
is a quadrilateral with two pairs of adjacent, congruent sides.
-
One diagonal of a kite bisects the other diagonal.
::一只风筝的对角线 另一只对角线的对角线 -
The diagonals of a kite are perpendicular.
::风筝的对角是垂直的。 -
One diagonal of a kite bisects its angles.
::风筝两面的对角 将它的角度分解成两面 -
A kite has one pair of opposite angles congruent.
::风筝有一对相反角度的对立面
::风筝是一种四边形, 配有两对相邻、 相近的两面。 一对风筝的对角分解了另一对对角。 一对风筝的对角是垂直的。 一对风筝的对角是垂直的。 一对风筝的对角是其角度的对角。 一对风筝的对角是相近的对角。 -
One diagonal of a kite bisects the other diagonal.
Review
::审查审查审查审查1. True or false: A rectangle is always a square.
::1. 真实或虚假:矩形始终是方形。2. True or false: A rhombus is always a parallelogram.
::2. 真实或虚假:暴风雪总是平行图。3. True or false: A square is always a rectangle.
::3. 真实或虚假:方形总是矩形。4. True or false: A kite is always a quadrilateral.
::4. 真实的或虚假的:风筝始终是四边形。Name each shape below based on its markings as precisely as you can. Don't assume that the shape is drawn to scale.
::根据每个形状的标记, 请尽可能精确地在下面命名每个形状。 不要假设形状是被拉到比例的 。5.
6.
7.
8.
For each quadrilateral below, name the shape. Then, solve for .
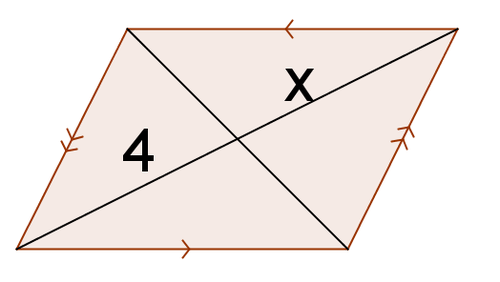
::对于以下的每个四边形, 命名形状。 然后, 解答 x 。9.
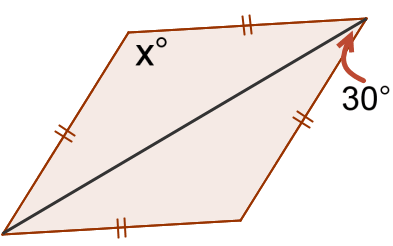
10.
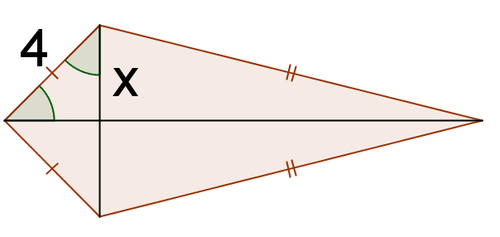
11.
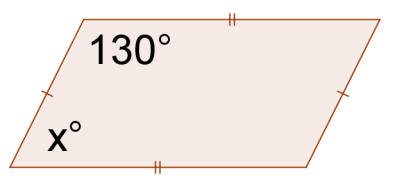
12.
13. Earlier you proved that if points and are midpoints on the edges of parallelogram then Given this, prove that .
::13. 早些时候,你证明如果F点和G点是ABCD平面边缘的中点,那么“AGF+GAD”。 有鉴于此,你证明FG'AD'。14. The midpoints of each of the sides of rectangle have been connected, as shown below. Make a conjecture about the inner quadrilateral that has been formed.
::14. 如下文所示,矩形ABCD两侧的中点相互连接,对所形成的内四边作出推测。15. Prove your conjecture from #14.
::15. 从14号证明你的猜想。16. Given: ; ;
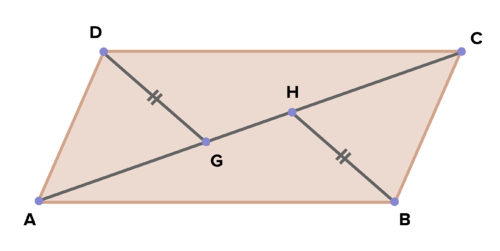
::16. 鉴于:AH ZGC;DG HB;DG HBProve: is a parallelogram
::证明: ABCD 是平行图17. Given: is a parallelogram;
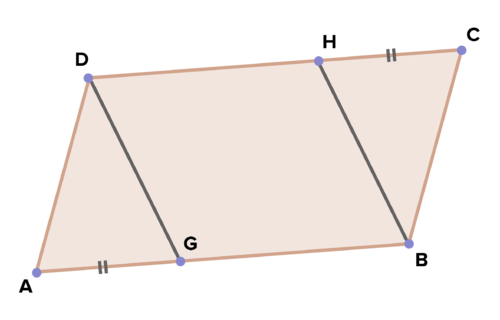
::17. 参考:ABCD是一个平行图;AG CHProve: is a parallelogram
::证明: DGBH 是一个平行图示Review (Answers)
::审查(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
Parallelogram Theorem #1
: Each
diagonal
of a
divides the parallelogram into two
congruent
triangles.