6.3A 三角相似性-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节AA三角相似性

  折叠 展开

  AA三角相似性

  播放段落

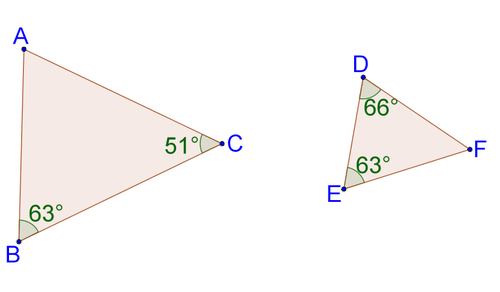
  If two triangles are similar , it means that all corresponding angle pairs are congruent and all corresponding sides are proportional . However, in order to be sure that two triangles are similar, you do not necessarily need to have information about all sides and all angles . 
  ::如果两个三角形相似, 这意味着所有相应的角对是相近的, 所有对应的边是比例的。 但是, 为了确定两个三角形是相似的, 您并不一定需要获得关于所有边和所有角的信息 。

  播放段落
  • The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar.
    ::三角形相似性AA标准规定,如果两个三角形有两对相近角,三角形就相似。

  播放段落

  This statement can be expressed as follows:
  ::这一陈述可表述如下:

  播放段落

  If two triangles $\begin{align*}ABC\end{align*}$ and $\begin{align*}DEF\end{align*}$ are such that $\begin{align*}\angle A = \angle D\end{align*}$ , and  $\begin{align*}\angle B = \angle E\end{align*}$ ,  then   $\begin{align*}\angle C = \angle F\end{align*}$ ,
  ::如果两个三角的ABC和DEF 都达到AQD和BBE 然后是CF

  播放段落

  and  $\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ ,  indicating  that   $\begin{align*}\frac{BC}{EF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AC}{DF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AB}{DE}\end{align*}$
  ::以及 ABC-DEF, 表明BCEF=ACDF=ABDE

  ---

  播放段落

  AA Triangle Similarity
  ::AA三角相似性

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle  $\begin{align*}ABC\end{align*}$  and observe the other triangle  $\begin{align*}DEF\end{align*}$  change accordingly to remain similar.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色顶部以重塑三角形ABC,并观察其他三角形的DEF相应变化以保持相似。

  播放段落

  1. Consider the triangles below. Dilate $\begin{align*}\triangle ABC\end{align*}$ with a scale factor of $\begin{align*}\frac{FE}{AB}\end{align*}$ to create $\begin{align*}\triangle A^\prime B^\prime C^\prime.\end{align*}$  What do you know about the sides and angles of $\begin{align*}\triangle A^\prime B^\prime C^\prime?\end{align*}$
  ::1. 考虑下方三角形。将 QABC 与 FEAB 比例因数相配,以创建 QABC。你对 QABC 的侧面和角度了解多少?

  

  播放段落

  Below, $\begin{align*}\triangle ABC\end{align*}$ is dilated about point $\begin{align*}P\end{align*}$ with a scale factor of $\begin{align*}\frac{FE}{AB}\end{align*}$ to create $\begin{align*}\triangle A^\prime B^\prime C^\prime.\end{align*}$
  ::以下为“ABC”扩展至P点,其比例系数为“FEAB”,以创建“A'B'C”。

  播放段落

  are congruent after a dilation is performed, so $\begin{align*}\angle B \cong \angle B^\prime.\end{align*}$  Therefore, $\begin{align*}\angle B^\prime \cong \angle E\end{align*}$ as well.
  ::进行比照后是相同的, 所以 B B。 因此, B E 也是一样 。

  播放段落

  Similarly, $\begin{align*}\angle A \cong \angle A^\prime,\end{align*}$  and therefore $\begin{align*}\angle A^\prime \cong \angle F\end{align*}$ .
  ::同样,AAAAA,因此AAAF。

  播放段落

  Because the scale factor was $\begin{align*}\frac{FE}{AB}\end{align*}$ , you know that  $\begin{align*}A^\prime B^\prime=\frac{FE}{\cancel{AB}} \cdot \cancel{AB}=FE.\end{align*}$
  ::因为比额表系数是FEAB, 你知道A'B'FEABAB=FE。

  播放段落

  Therefore:  $\begin{align*}\overline{A^\prime B^\prime} \cong \overline{FE}.\end{align*}$
  ::因此:A'B'FE。

  播放段落

  2) P rove that $\begin{align*}\triangle ABC \sim \triangle FED.\end{align*}$
  ::2) 证明ABCFED。

  播放段落

  Y ou know now that $\begin{align*}\angle B^\prime \cong \angle E\end{align*}$ , $\begin{align*}\angle A^\prime \cong \angle F\end{align*}$ and $\begin{align*}\overline{A^\prime B^\prime} \cong \overline{FE}\end{align*}$ . This means that $\begin{align*}\triangle A^\prime B^\prime C^\prime \cong \triangle FED\end{align*}$ by $\begin{align*}ASA \cong\end{align*}$ . Therefore, there must exist a sequence of rigid transformations that will carry $\begin{align*}\triangle FED\end{align*}$ to $\begin{align*}\triangle A^\prime B^\prime C^\prime\end{align*}$ .
  ::现在你知道"B"、"A"、"A"、"B"和"A"了。这意味着"A"B'C" 和"A'C"。因此,必须存在一系列的僵硬变换, 将"FED"带到"A'B'C"。

  播放段落

  $\begin{align*}\triangle ABC \sim \triangle FED\end{align*}$ because a series of rigid transformations will carry $\begin{align*}\triangle FED\end{align*}$ to $\begin{align*}\triangle A^\prime B^\prime C^\prime\end{align*}$ , and then a dilation will carry $\begin{align*}\triangle A^\prime B^\prime C^\prime\end{align*}$ to $\begin{align*}\triangle ABC\end{align*}$ .
  ::ABC=FED,因为一系列的硬质变换 将携带FEED到AAB=C}然后放大 将携带AB=C=ABC

  播放段落

  All that was known about the original two triangles in #1 was two pairs of congruent angles. Therefore, you have proved that AA is a criterion for triangle similarity.
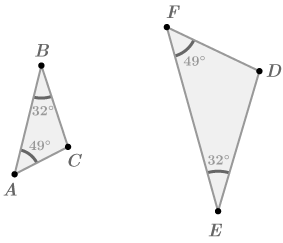
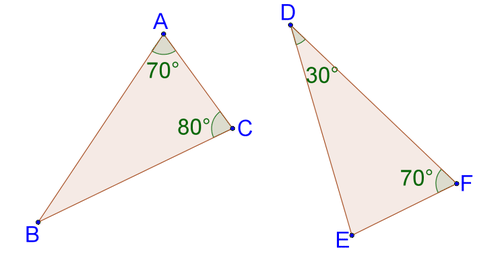
  ::在 # 1 中, 最初的两个三角形的已知点只有两对相似角度。 因此, 您已经证明了 AAA 是三角形相似性的标准 。

  播放段落

  3) Are the triangles below similar? Explain.
  ::3) 三角形以下是否相似?请解释。

  播放段落

  One pair of angles is marked as being congruent.
  ::一对角度被标记为相似 。

  播放段落

  You also  know   another pair of congruent angles due to the in the center of the picture.
  ::您还知道另一对相近角度, 是由图片的中间部分造成的。

  播放段落

  Therefore, the triangles are similar by $\begin{align*}AA \sim.\end{align*}$
  ::因此,三角形与AAQQ相似。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Why don't you have to verify that all three pairs of corresponding angles are congruent in order to show that two triangles are similar?
  ::你何不核实这三对对应角度是否吻合 才能证明两个三角形是相似的呢?

  播放段落

  If two pairs of angles are congruent, then three pairs of angles must be congruent due to the fact that the sum of the measures of the interior angles of a triangle is $\begin{align*}180^\circ.\end{align*}$
  ::如果两对角度一致,那么三对角度必须一致,因为三角形内角的测量总和是180。

  播放段落

  Therefore, three pairs of congruent angles is more information than you need.
  ::因此,三对一致的角度 比你需要的信息更多。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Prove that $\begin{align*}\triangle CBA \sim \triangle GDA\end{align*}$ .
  ::证明那个CBAGDA

  播放段落

  Note that $\begin{align*}\overline{CB} \ \| \ \overline{GD}\end{align*}$ . This means that $\begin{align*}\angle AGD\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle ACB\end{align*}$ because they are corresponding angles. $\begin{align*}\angle A\end{align*}$ is shared by both triangles. Two pairs of angles are congruent, so $\begin{align*}\triangle CBA \sim \triangle GDA\end{align*}$ by $\begin{align*}AA \sim.\end{align*}$
  ::注意CB = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

  播放段落

  Example 3
  ::例3

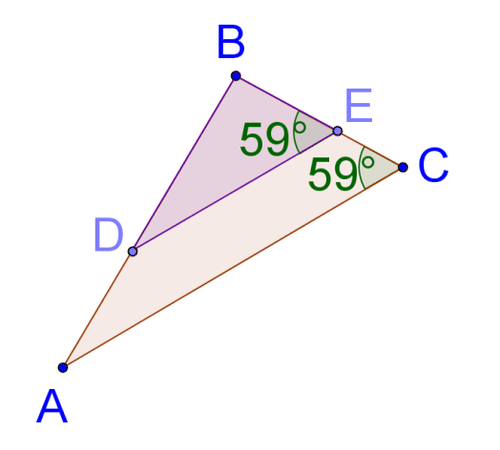
  播放段落

  Prove that $\begin{align*}\triangle CBA \sim \triangle CEF\end{align*}$ .
  ::证明一下CBACEF

  播放段落

  Note that $\begin{align*}\overline{AB} \ \| \ \overline{FE}\end{align*}$ . This means that $\begin{align*}\angle BAC\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle EFC\end{align*}$ because they are corresponding angles. $\begin{align*}\angle C\end{align*}$ is shared by both triangles. Two pairs of angles are congruent, so $\begin{align*}\triangle CBA \sim \triangle CEF\end{align*}$ by $\begin{align*}AA \sim.\end{align*}$
  ::注意 AB {FE} 。 这表示 {BAC {EFC} 因为它们是相应的角度 。 <C} 由两个三角共有。 两对角是相同的, 所以 {CBA} {CEF by AA} 。

  播放段落

  Example 4
  ::例4

  播放段落

  Prove that $\begin{align*}\triangle CBA \sim \triangle GHF\end{align*}$ .
  ::证明那个"CBAGHF"

  播放段落

  In Example #2 you found that $\begin{align*}\angle AGD\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle ACB\end{align*}$ . In Example #3 you found that $\begin{align*}\angle BAC\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle EFC\end{align*}$ . Two pairs of angles are congruent, so $\begin{align*}\triangle CBA \sim \triangle GHF\end{align*}$ by $\begin{align*}AA \sim.\end{align*}$
  ::在例#2中,你发现了AGDACB。在例#3中,你发现了BACEFC。两对角度是相容的,所以AAQQ的CBAGHF。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  播放段落

  AA Similarity
  ::AA 类似性

  Summary

  播放段落 If two triangles are similar , it means that all corresponding angle pairs are congruent and all corresponding sides are proportional.  ::如果两个三角形相似,则意味着所有相应的角对均匀,所有相应的边均成正比。 播放段落 The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar. ::三角形相似性AA标准规定,如果两个三角形有两对相近角,三角形就相似。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. What does AA stand for? How is it used?
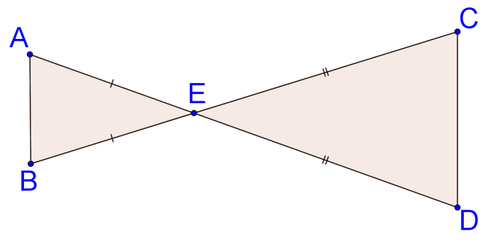
  ::1. AA代表什么?它是如何使用的?

  播放段落

  2. Draw an example of two triangles that must be similar due to AA.
  ::2. 举两个三角形的例子,这两个三角形因AA而必须相似。

  播放段落

  For each pair of triangles below, state if they are congruent, similar or not enough information. If they are similar or congruent, write a similarity or congruence statement. Explain your answer.
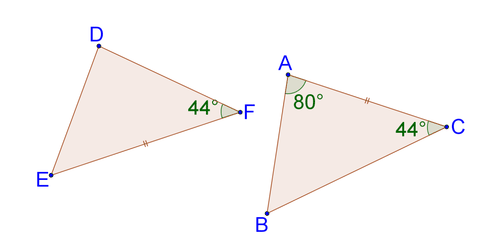
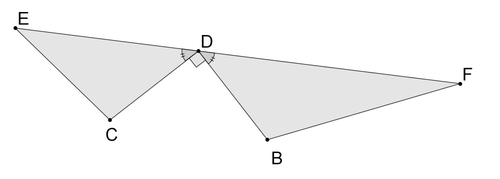
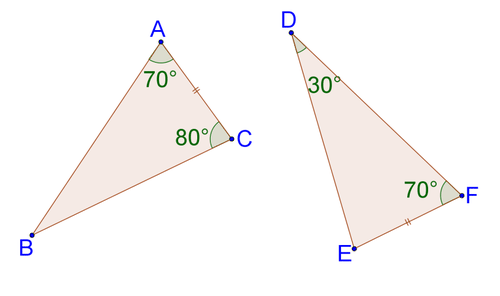
  ::对于下面的每对三角形,请说明它们是否一致、相似或不够充分的信息。如果它们相似或一致,请写一个相似或一致的语句。请解释您的回答。

  3.

  

  4.

  

  5.

  

  6.

  

  7.

  

  8.

  

  9.

  

  10.

  

  11.

  

  12.

  

  13.

  

  播放段落

  14. Can you use the AA criteria to show that other shapes besides triangles are similar?
  ::14. 您能否使用 AA 标准来显示除三角形之外的其他形状相似?

  播放段落

  15. Use similarity transformations to explain in your own words why two triangles with two pairs of congruent angles must be similar.
  ::15. 使用相似性转换用你自己的字眼来解释为什么两个三角形和两对相同角度必须相似。

  播放段落

  16. Prove that if two triangles have two pairs of congruent angles, the third pair must be congruent.
  ::16. 证明如果两个三角形有两对相同角度,第三对必须是相同的。

  播放段落

  17. For the two triangles below, corresponding angles are congruent. Is there a sequence of transformations that would map one to the other? Describe it. Are the triangles similar? Explain.
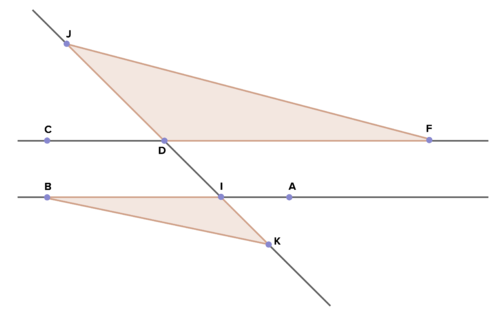
  ::17. 对于以下两个三角形,相应的角度是相同的。是否有一个变形序列可以绘制一个变形图到另一个变形图?描述一下。三角形相似吗?解释一下。

  

  播放段落

  18. Given: $\begin{align*}\overline{CF} \parallel \overline{BA}\end{align*}$ ; $\begin{align*}\angle DFJ \cong \angle IBK\end{align*}$
  ::18. 鉴于:CF_BA;DFJ_BBK

  播放段落

  Prove: $\begin{align*}\triangle DFJ \cong \triangle IBK\end{align*}$ .
  ::证明:"DFJIBK"。

  

  播放段落

  19. Given: $\begin{align*}\overline {DE} \parallel \overline {BC}\end{align*}$
  ::19. 鉴于:

  播放段落

  Prove: $\begin{align*}\triangle ABC \cong \triangle ADE\end{align*}$ .
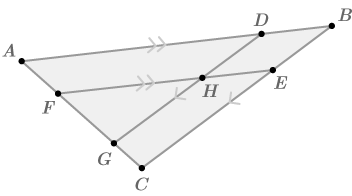
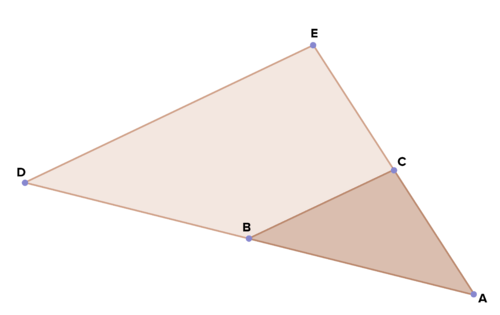
  ::证明:ABCADE。

  

  播放段落

  20. Prove the three triangles in the diagram below are similar to each other.
  ::20. 证明下图中的三个三角是相似的。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。