6.5 SSS 三角相似性-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节SSS SSS 三角相似性

  折叠 展开

  SSS SSS 三角相似性

  S imilar triangles  have congruent  corresponding angle pairs  and proportional corresponding sides .

  Y ou do not necessarily need to have information about all sides and all angles in order to be certain that two triangles are similar . 

  播放段落
  • The criterion for triangle similarity states that if three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar.
    ::三角形相似性的标准是,如果一个三角形的三边与另一个三角形的三边成正比,那么三角形是相似的。

  播放段落

  This statement can be expressed as follows:
  ::这一陈述可表述如下:

  播放段落

  If two triangles $\begin{align*}ABC\end{align*}$ and $\begin{align*}DEF\end{align*}$ are such that  $\begin{align*}\frac{BC}{EF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AC}{DF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AB}{DE}\end{align*}$ , then  $\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ .
  ::如果ABC和DEF两个三角如ABC和DEF,则BCEF=ACDF=ABDE,则ZABC=DEF。

  播放段落

  This implies that $\begin{align*}\angle A = \angle D\end{align*}$ , $\begin{align*}\angle B = \angle E\end{align*}$ and $\begin{align*}\angle C = \angle F\end{align*}$ .
  ::这意味着“AD”、“BE”和“CF”。

  ---

  播放段落

  SSS Triangle Similarity
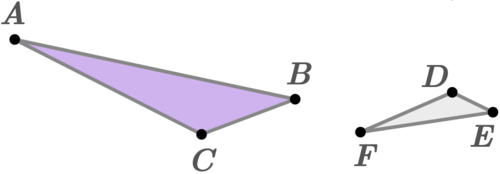
  ::SSS SSS 三角相似性

  播放段落

  Click the small blue arrow next to the image below, and then drag the orange vertices to reshape the triangle $\begin{align*}ABC.\end{align*}$   O bserve triangle $\begin{align*}DEF\end{align*}$ changing accordingly to remain similar.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色的脊椎重塑三角形ABC。观察三角形DEF相应变化以保持相似 。

  播放段落

  Try it yourself - See that the side lengths of  $\begin{align*}\triangle ABC,\end{align*}$  multiplied by 1/2, always yield the corresponding side lengths of $\begin{align*}\triangle DEF:\end{align*}$  
  ::试试你自己 - 注意 QABC 的侧边长度乘以 1/2 , 总是产生 QDEF 的相应侧边长度 :

  播放段落
  • When $\begin{align*}\overline{AB} = 17,\end{align*}$  corresponding side  $\begin{align*}\overline{DE} = 8.5.\end{align*}$  
    •   $\begin{align*}\large{17 \left( \frac{1}{2} \right) = 8.5} \vphantom{{\sum}}\end{align*}$  
    
    ::当AB=17时,对应方是8.5 17(12)=8.5
  播放段落
  • When $\begin{align*}\overline{AC} = 11.6,\end{align*}$  corresponding side $\begin{align*}\overline{DF}=5.8.\end{align*}$  
    •   $\begin{align*}\large{11.6 \left( \frac{1}{2} \right) = 5.8} \vphantom{{\sum}}\end{align*}$  
    
    ::当AC=11.6时,对应方的DF=5.8。 11.6(12)=5.8
  播放段落
  • When $\begin{align*}\overline{BC} = 18.4,\end{align*}$  corresponding side $\begin{align*}\overline{EF}=9.2.\end{align*}$  
    •   $\begin{align*}\large{18.4 \left( \frac{1}{2} \right) = 9.2} \vphantom{{\sum}}\end{align*}$    
    
    ::当“BC=18.4”时,对应方的EF=9.2 18.4(12)=9.2

   

   

  播放段落

  Consider  a couple of problems regarding SSS triangle similarity:
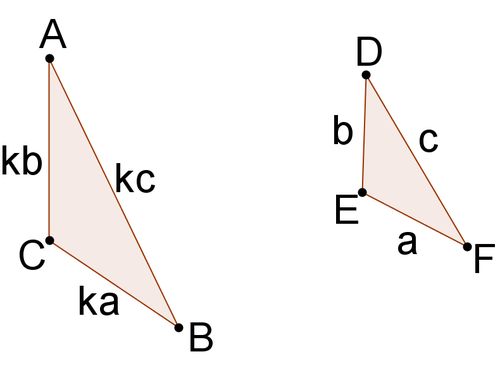
  ::考虑几个有关SSS三角相似性的问题:

  播放段落

  1.  In the triangles below,  $\begin{align*}\frac{AB}{FE}=\frac{CA}{DF}=\frac{CB}{DE}=k.\end{align*}$
  ::1. 在以下三角形中,ABFE=CADF=CBDE=K。

  

  播放段落

  Dilate $\begin{align*}\triangle DEF\end{align*}$   by a scale factor of $\begin{align*}k\end{align*}$   to create $\begin{align*}\triangle D^\prime E^\prime F^\prime.\end{align*}$   What can you say about the relationship between the sides of $\begin{align*}\triangle D^\prime E^\prime F^\prime\end{align*}$  and $\begin{align*}\triangle ABC?\end{align*}$
  ::以 k 的比例因子来将 DEF 扩展为 D EF。 您对 D EF 和 ABC 之间的关系有什么看法 ?

  播放段落

  Below, $\begin{align*}\triangle DEF\end{align*}$ is dilated about point $\begin{align*}P\end{align*}$ with a scale factor of $\begin{align*}k\end{align*}$ to create $\begin{align*}\triangle D^\prime E^\prime F^\prime.\end{align*}$
  ::DEF在P点上放大, 比例因子为 k , 以创建 D§E§F§。

  播放段落

  The scale factor is $\begin{align*}k\end{align*}$ , which is the ratio of the lengths of the corresponding sides of the two similar triangles :  $\begin{align*}\frac{AB}{FE}\end{align*}$ ,   $\begin{align*}\frac{CA}{DF}\end{align*}$ and $\begin{align*}\frac{CB}{DE}.\end{align*}$
  ::比例系数为k,即两个类似三角形(ABFE、CADF和CBDE)对应侧长度之比。

  播放段落

  This means:
  ::这意味着:

  播放段落
  •   $\begin{align*}D^\prime F^\prime=k\cdot DF=\frac{CA}{\cancel{DF}}\cdot \cancel{DF}=CA \vphantom{\sum^X_X}\end{align*}$  :  Therefore, $\begin{align*}\overline{D^\prime F^\prime} \cong \overline{CA}\end{align*}$ .
    ::DF=CADF=CAX=CAX=CAX:所以,FA=CA。
  播放段落
  •   $\begin{align*}D^\prime E^\prime=k\cdot DE=\frac{CB}{\cancel{DE}}\cdot \cancel{DE}=CB \vphantom{\sum^X_X}\end{align*}$  :  Therefore, $\begin{align*}\overline{D^\prime E^\prime} \cong \overline{CB}\end{align*}$ .
    ::D'E'k'DE=商用八溴二苯醚=CBXX:因此,可以。
  播放段落
  •   $\begin{align*}F^\prime E^\prime=k\cdot FE=\frac{AB}{\cancel{FE}}\cdot \cancel{FE}=AB \vphantom{\sum^X_X}\end{align*}$  :   Therefore, $\begin{align*}\overline{F^\prime E^\prime} \cong \overline{AB}\end{align*}$ .
    :笑声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声)

  播放段落

  2. Use your work from the previous problem to prove that $\begin{align*}\triangle ABC\thicksim\triangle FED\end{align*}$ .
  ::2. 利用上一个问题中你的工作证明是ABC-FED。

  播放段落

  You know that $\begin{align*}\overline{D^\prime F^\prime}\cong \overline{CA}\end{align*}$ , $\begin{align*}\overline{D^\prime E^\prime}\cong \overline{CB}\end{align*}$ and $\begin{align*}\overline{F^\prime E^\prime}\cong \overline{AB}\end{align*}$ . This means $\begin{align*}\triangle ABC \cong \triangle F^\prime E^\prime D^\prime\end{align*}$ by SSS   $\begin{align*}\! \cong.\end{align*}$
  ::你知道这很重要,这代表SSS的"ABC'F'D"

  播放段落

  Therefore, there must exist a sequence of rigid transformations that will carry $\begin{align*}\triangle ABC\end{align*}$ to $\begin{align*}\triangle F^\prime E^\prime D^\prime.\end{align*}$
  ::因此,必须存在一系列的僵硬变换,将ABC 带到 QFED。

  播放段落

  $\begin{align*}\triangle ABC\thicksim\triangle FED\end{align*}$ because a series of rigid transformations will carry $\begin{align*}\triangle ABC\end{align*}$ to $\begin{align*}\triangle F^\prime E^\prime D^\prime\end{align*}$ , and then a dilation will carry $\begin{align*}\triangle F^\prime E^\prime D^\prime\end{align*}$ to $\begin{align*}\triangle FED\end{align*}$ .
  ::ABC=FEED,因为一系列的硬质变换 将会把ABC 带到FFED=DD}然后一个放大镜会把FED 带到FEED=FEED=FED。

  播放段落

  All that was given  regarding the original two triangles was that they have three pairs of proportional sides. You have proved that  SSS  is a criterion for triangle similarity.
  ::关于最初的两个三角形,所给出的只是它们有三对成比例边。你已经证明SSS是三角形相似性的标准。

  ---

  播放段落

  Use SSS to Prove Triangles are Similar
  ::使用 SSS 来验证三角形相似

  播放段落

  You want to show that the triangles below are similar by SSS  $\begin{align*}\! \thicksim.\end{align*}$  What additional information do you need?
  ::您想要显示下面的三角形与 SSS Q 相似。 您需要哪些补充信息 ?

  播放段落

  You have three side lengths for $\begin{align*}\triangle ABC,\end{align*}$  and you are given  $\begin{align*}\frac{AB}{FE}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AC}{FD}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}3\end{align*}$ .
  ::“ABC”有三个侧长,给您提供ABFE=ACFD=3。

  播放段落

  Since $\begin{align*}CB=6\end{align*}$ , you need to know that $\begin{align*}DE=2\end{align*}$ (so that $\begin{align*}\frac{CB}{DE}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}3\end{align*}$ ) in order to show that the triangles are similar by SSS $\begin{align*}\! \thicksim.\end{align*}$
  ::自CB=6以来,你需要知道DE=2(因此CBDE=3),以表明SSS=3的三角形相似。

   

   

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  How can you use the SSS similarity criterion to show that the triangles below are similar?
  ::您如何使用 SSS 相似性标准来显示下面的三角形相似 ?

  

  播放段落

  Only two pairs of sides and  one pair of non- included angles are given. You can't say these triangles are similar by SSA, because that is not a criterion for triangle similarity. However, because these are right triangles , you know that the third side of each triangle can be found with the Pythagorean Theorem .
  ::仅给出两对边和一对未包含角度。 您不能说这些三角形与 SSA 相似, 因为这不是三角形相似的标准 。 但是, 由于这些三角形是右三角形, 您知道每个三角形的第三面可以与 Pythagorean Theorem 一起找到 。

  播放段落

  $\begin{align*}\bullet \ \text{ Smaller triangle: }12^2+x^2=15^2\rightarrow & x = \sqrt{{15}^2 - {12}^2} \\ & x = \sqrt{225 -144} \\ & x= \sqrt{81}\\ & x = 9\\\end{align*}$
  ::* 小三角形:122+x2=152x 152-122x225-144x81x=9

  播放段落

  $\begin{align*}\bullet \text{ Larger triangle: } \ 36^2+x^2=45^2\rightarrow & x=\sqrt{{45}^2- {36}^2}\\ & x = \sqrt{2025 - 1296} \\ & x = \sqrt{729}\\ & x = 27 \\\end{align*}$
  ::* 大三角形:362+x2=452xx*452-362x}2025-1296x=729x=27

  播放段落

  All three pairs of sides are proportional with a ratio of 3. Therefore, the triangles are similar due to SSS.
  ::所有三对两侧的比例为3。 因此,三角形与特殊安保服务相似。

  播放段落

  Example 2
  ::例2

  播放段落

  Are the triangles similar? Explain.
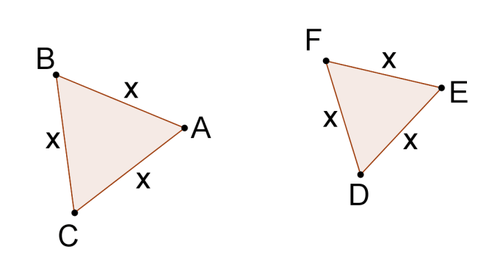
  ::三角形相似吗?

  播放段落

  All three sides of each triangle are the same . The ratio between each pair of sides is $\begin{align*}\frac{4x}{x}=4.\end{align*}$  Because three pairs of sides are proportional, the triangles are similar by SSS.
  ::每个三角形的所有三边都是相同的。 每两边的比重是 4xx=4。 因为三对的边是比例的, 三角形与 SSS 相似 。

  播放段落

  Example 3
  ::例3

  播放段落

  Are the triangles similar? Explain.
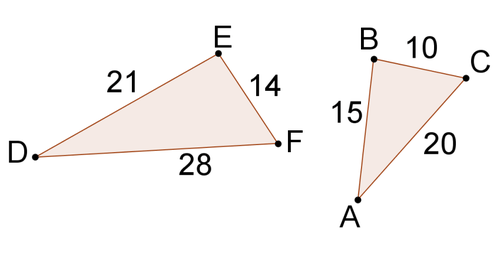
  ::三角形相似吗?

  播放段落

  Match each side of one triangle with the corresponding side on the other . Check all three ratios:
  ::将一个三角形的两侧与另一个三角形对应的一侧匹配。 请检查所有三个比例 :

  播放段落
  • $\begin{align*}\frac{DF}{AC}\end{align*}$ $\begin{align*}= \frac{18}{6} = 3\\ \ \\\end{align*}$
    ::DFAC=186=3
  播放段落
  • $\begin{align*}\frac{DE}{AB}\end{align*}$ $\begin{align*}=\frac{15}{5}=3\end{align*}$
    ::DEB=155=3
  播放段落
  • $\begin{align*}\frac{EF}{BC}\end{align*}$ $\begin{align*}\ \\ = \frac{6}{4}= 1.5\end{align*}$
    ::EFBC=64=1.5

  播放段落

  Because the three pairs of sides are not proportional (the ratios are not the same - two are  $\begin{align*}\frac31\end{align*}$  and one is $\begin{align*}\frac32\end{align*}$ ), the triangles are not similar.
  ::因为三对对配对不相称(比率不同——两对31,一对32),三角形并不相似。

  播放段落

  Example 4
  ::例4

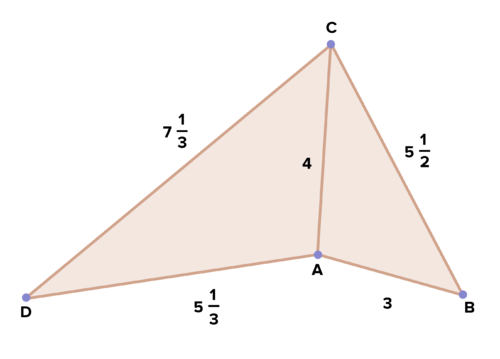
  播放段落

  What additional information is necessary to show that the triangles below are similar by SSS similarity? 
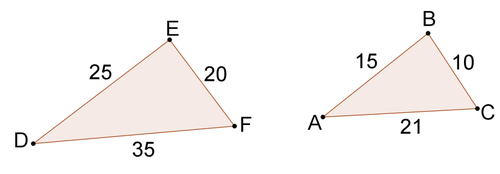
  ::需要哪些补充信息来显示以下三角形与SSS相似性相似?

  播放段落

  Look for two pairs of sides with lengths in the same ratio.
  ::寻找两对长度相同比例的对立方。

  播放段落
  • $\begin{align*}\frac{DE}{AB}\end{align*}$ $\begin{align*}=\frac{25}{15}=\frac{5}{3}\\ \ \\\end{align*}$
    ::DEB=2515=53
  播放段落
  • $\begin{align*}\frac{DF}{AC}\end{align*}$ $\begin{align*}=\frac{35}{21}=\frac{5}{3}\end{align*}$
    ::DFAC=3521=53

  播放段落

  The common ratio is $\begin{align*}\frac{5}{3}\end{align*}$ . This means that if the triangles are indeed similar,  $\begin{align*}\frac{EF}{BC}\end{align*}$ must equal $\begin{align*}\frac{5}{3}\end{align*}$ as well.

  $$\begin{align*}\frac{15}{BC}&=\frac{5}{3}\\ 45 &=5(BC) \vphantom{\frac{-}{.}} \\ 9 &=BC\end{align*}$$
  ::共同比率是53,这意味着,如果三角形确实相似,则EFBC必须等于53,还有15BC=5345=5(BC)-9=BC。

  播放段落

  For the triangles to be similar by SSS similarity, you need to know that $\begin{align*}BC=9.\end{align*}$
  ::要让三角形与 SSS 相似性相似, 您需要知道 BC=9 。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  播放段落

  SSS Similarity
  ::SSSS 相似性

   

   

  Summary

  播放段落 The SSS criterion for triangle similarity states that if three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar. ::三角形相似性SSS标准规定,如果一个三角形的三边与另一个三角形的三边成正比,那么三角形是相似的。

  ---

  播放段落

  Reviews
  ::审查

  播放段落

  1. What does SSS stand for? What does it have to do with similar triangles?
  ::1. SSS代表什么?它与类似的三角有什么关系?

  播放段落

  2. Draw an example of two triangles that must be similar due to SSS.
  ::2. 举两个三角形的例子,这两个三角形必须因特殊安全服务而相似。

  播放段落

  For each pair of triangles below state if they are similar, congruent, or if there is not enough information to specify. If they are similar or congruent, write a similarity or congruence statement.
  ::对于以下每对三角形,如果它们相似、相似,或者没有足够信息可以指定,则要说明。如果它们相似或一致,请写一个相似或一致的语句。

  3.

  

  4.

  

  5.

  

  6.

  

  7.

  

  播放段落

  8. What does the previous problem tell you about equilateral triangles?
  ::8. 前一个问题对等三角形有什么看法?

  播放段落

  9. How are the perimeters of two similar triangles related?
  ::9. 两个类似三角形的周边如何相关?

  播放段落

  10. One triangle has side lengths of 6, 8 and 10. A similar triangle has a perimeter of 60. What are the lengths of the sides of the similar triangle?
  ::10. 一个三角形的侧边长度为6、8和10。 一个类似的三角形的周边长度为60。 类似三角形两侧的长度是多少?

  播放段落

  11. One triangle has side lengths of 7, 8 and 14. A similar triangle has a perimeter of 87. What is the ratio between corresponding sides?
  ::11. 一个三角形的侧边长度为7、8和14。 一个类似的三角形的周边长度为87。 对应方之间的比例是多少?

  播放段落

  12. One triangle has side lengths of 2, 4 and 4. A similar triangle has a perimeter of 30. What are the lengths of the sides of the similar triangle?
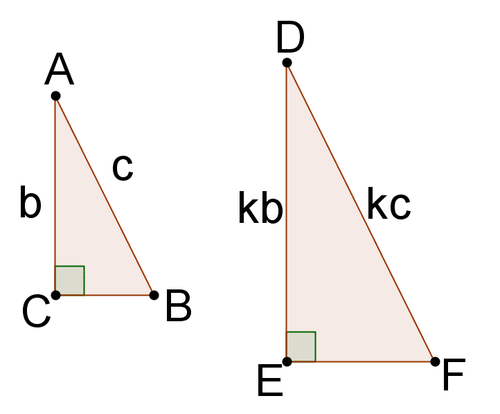
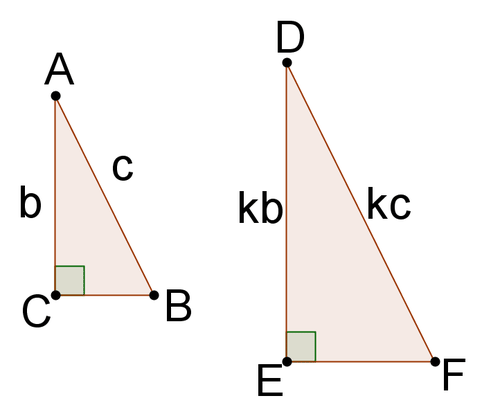
  ::12. 一个三角形的侧长为2、4和4。 一个类似的三角形的周边长度为30。 类似三角形两侧的长度是多少?

  播放段落

  13. Find the length of the unmarked side of each triangle in terms of $\begin{align*}c\end{align*}$ , $\begin{align*}b\end{align*}$ and $\begin{align*}k\end{align*}$ .
  ::13. 以 c、 b 和 k 来查找每个三角形无标记方的长度。

  

  播放段落

  14. P rove that the two triangles are similar. You may reference your prior work. What does this tell you about one method for proving that right triangles are similar?
  ::14. 证明这两个三角是相似的。您可以参考您先前的工作。这告诉您,用一种方法来证明右三角是相似的吗?

  

  播放段落

  15. Show how the SSS criterion for triangle similarity works: use transformations to help explain why the triangles below are similar. Hint: See  the examples in the lesson for help.
  ::15. 显示三角相近性 SSS 标准是如何运作的:使用变换来解释以下三角为何相似。 提示: 请参见课程中的帮助示例 。

  

  播放段落

  16. Are all congruent triangles similar? Are all similar triangles congruent? Explain.
  ::16. 所有相似的三角形是否都相似?所有相似的三角形是否都相似?解释。

  播放段落

  17. We use the abbreviations SSS and SAS for similarity and congruence. What do these expressions mean?
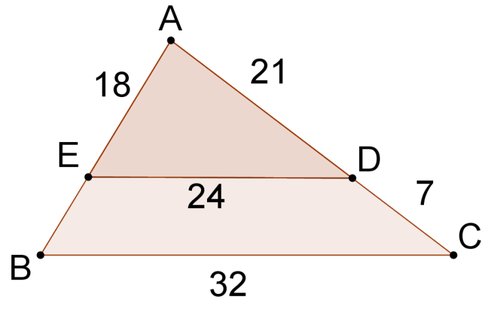
  ::17. 我们使用缩略语SSS和SAS的相似性和一致性,这些表达方式意味着什么?

  播放段落

  18. Given the diagram as shown below, determine if the triangles are similar or not. Explain.
  ::18. 鉴于下图所示,请确定三角形是否相似,请解释。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.
  ::要查看本书的答案键, 请在“ ” 选项下点击答案键 。