6.7 类似三角的应用-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节类似三角的应用

  折叠 展开

  类似三角的应用

  Similar triangles have congruent and proportional  corresponding sides .

  There are three common sets of criteria for proving that triangles are similar:

  播放段落
  1. AA: If two triangles have two pairs of congruent angles , then the triangles are similar. To learn more about AA Triangle Similarity (and play with the interactive), click  .  
     
     
     ::AA: 如果两个三角形有两对相近角度, 那么三角形是相似的。 要了解更多关于 AA 三角形相似性( 并与互动游戏一起玩) , 请单击 。
  播放段落
  2. : If two sides of one triangle are proportional to two sides of another triangle and their included angles are congruent, then the triangles are similar. To  learn more about  SAS Triangle Similarity, and play with an interactive, click  . 
     
     
     :::如果一个三角形的两面与另一个三角形的两面成正比,而且它们包含的角是相同的,那么三角形是相似的。要更多地了解SAS三角形的相似性,请单击互动游戏。
  播放段落
  3. : If three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar. To play with an interactive and learn more about SSS Triangle Similarity, click  . 
     
     
     :::如果一个三角形的三边与另一个三角形的三边成正比,则三角形是相似的。要与互动游戏并更多地了解 SSS 三角相似性,请单击 。

  ---

  播放段落

  Triangle Similarity  and 30-60-90 Triangles
  ::三角相近和30-60-90三角

  播放段落

  Once you know that two triangles are similar, you can use the fact that their corresponding sides are proportional and their corresponding angles are congruent to solve problems.
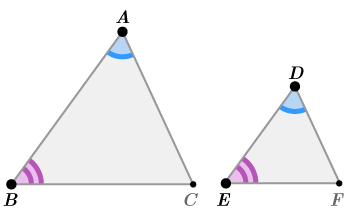
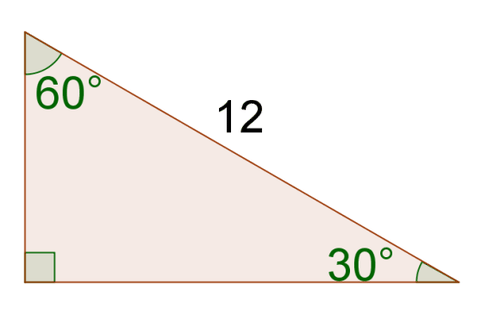
  ::一旦你知道两个三角形是相似的, 你可以使用一个事实, 即它们对应的两边是比例的, 它们对应的角度在解决问题上是一致的。

  播放段落

  Consider the triangles in the image below.
  ::考虑下方图像中的三角形 。

  播放段落

      a. Prove that the triangles are similar.
  ::a. 证明三角形相似。

  播放段落

  The triangles are similar by $\begin{align*}AA \sim\end{align*}$ because they have at least two pairs of congruent angles, i.e.,
  ::三角形与AA相似,因为它们至少有两对相近角度,即:

  播放段落

  $\begin{align*}\angle ABC = \angle DEF= 90^\circ\end{align*}$ , $\begin{align*}\angle BCA = \angle EFD = 30^\circ\end{align*}$ , $\begin{align*}\angle CAB = \angle FDE = 60^\circ\end{align*}$
  ::ABCDEF=90, BCEFD=30, CABFDE=60

  播放段落

      b. Use the Pythagorean Theorem to find $\begin{align*}DE\end{align*}$ .
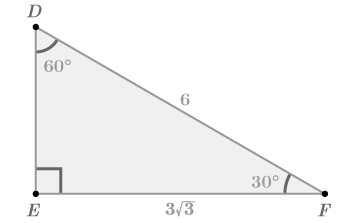
  ::b. 利用毕达哥里理论查找DE。

  播放段落

  According to the Pythagorean Theorem, in $\begin{align*}\triangle DEF\end{align*}$ :
  ::根据《毕达哥里安神论》,

  播放段落

  $\begin{align*}EF^2 + DE^2 & = FD^2\\ \left (3 \sqrt{3} \right )^2 + DE^2 &= 6^2 \\ (9\cdot 3) + DE^2 & = 6^2 \\ 27+DE^2 &= 36 \\ DE^2 & = 36 -27 \\ DE^2 &= 9 \\ DE &= 3 \end{align*}$
  ::EF2+DE2=FD2(33)2+DE2=62(93)+DE2=6227+DE2=36DE2=36-27DE2=9DE=3

  播放段落

      c. Use the fact that the triangles are similar to find the missing sides of $\begin{align*}\triangle ABC\end{align*}$ .
  ::c. 利用三角形相似这一事实来找到QABC缺失的侧面。

  播放段落

  $\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ , which means that the corresponding sides are proportional. Therefore,
  ::ABCDEF,这意味着对应的两面是成比例的。

  播放段落

  $\begin{align*}\frac{AB}{DE}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{BC}{EF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AC}{DF}\end{align*}$
  ::ABDEB = BCEF = ACDF = ABDEF = ABCEF = ACDF

  播放段落

  $\begin{align*}\frac{AC}{DF} = \frac{18}{6} = 3\end{align*}$ , so the scale factor is 3.
  ::ACDF=186=3,因此比额表系数为3。

  播放段落
  •    $\begin{align*}\frac{AB}{DE} = 3 \rightarrow \frac{AB}{3} = 3 \rightarrow AB = 9 \vphantom{\Huge{X}}\end{align*}$
    ::ABDE=3AB3=3ABB=9X
  播放段落
  •   $\begin{align*}\frac{BC}{EF} = 3 \rightarrow\frac{BC}{3 \sqrt{3}} = 3 \rightarrow BC = 9 \sqrt{3} \vphantom{\Huge{X}}\end{align*}$
    ::BCEF=3-BC3-3=3-BC=9-3X

  播放段落

  Triangles of this configuration are called 30-60-90 triangles because of their angle measures.
  ::此配置的三角因其角度大小而被称为 30- 60- 90 三角形。

  播放段落

      d. Explain why all 30-60-90 triangles are similar.
  ::d. 解释为什么所有30-60-90三角形都相似。

  播放段落

  All 30-60-90 triangles are similar by $\begin{align*}AA \sim\end{align*}$ because they all have at least two pairs of congruent angles.
  ::AA的所有30-60-90三角形都相似,因为它们至少有两对相同的角。

  ---

  播放段落

  30-60-90 Triangle Side Ratios
  ::30-60-90 三角边际比率

  播放段落

  1. F ind the ratios between the three sides of any 30-60-90 triangle . 
  ::1. 找出任何30-60-90三角形三边之间的比率。

  

  播放段落

  From the reference image: $\begin{align*}\triangle DEF\end{align*}$ has sides 
  $\begin{align*}DE = 3, \, EF= 3\sqrt{3},\end{align*}$  and  $\begin{align*}FD = 6.\end{align*}$  This ratio of $\begin{align*}3:3 \sqrt{3}:6\end{align*}$ reduces to $\begin{align*}1:\sqrt{3}:2.\end{align*}$
  ::从参考图象来看: " DEF " 的侧面是:DE=3,EF=3,33,FD=6。 3:3:3:6的比例降至1:3:2。

  播放段落

  The three sides of any 30-60-90 triangle will be in this ratio: $\begin{align*}\bf{1 : \sqrt{3} \, : \, 2.}\end{align*}$
  
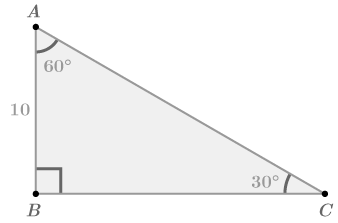
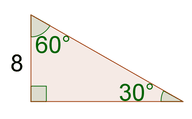
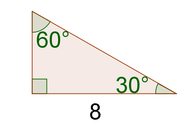
  ::任何30-60-90三角形的三边都将是这个比例:1:%3:2。

  播放段落

  2 . Find the missing sides of the triangle below.
  ::2. 找出以下三角形的缺失侧。

  

  播放段落

  The side opposite the $\begin{align*}30^\circ\end{align*}$ angle is the smallest side because $\begin{align*}30^\circ\end{align*}$ is the smallest angle. Therefore, the length of 10 corresponds to the length of 1 in the ratio $\begin{align*}1:\sqrt{3}:2\end{align*}$ . The scale factor is 10. The other sides of the triangle will be $\begin{align*}10 \sqrt{3 }\end{align*}$ and 20, because $\begin{align*}10:10 \sqrt{3}:20\end{align*}$ is equivalent to $\begin{align*}1: \sqrt{3}:2.\end{align*}$   $\begin{align*}BC=10 \sqrt{3}\end{align*}$ and $\begin{align*}AC=20.\end{align*}$
  ::30角对面是最小的一面, 因为30角是最小的。 因此, 10的长度相当于1: 3: 2. 比例的长度 1 : 3: 3。 比例系数是 10。 三角形的另一边是 10: 3: 3: 20, 因为 10: 10: 3: 3: 20 等于 1: 3: 2. BC= 10: 3 和 AC=20 。

  ---

  播放段落

  Similar Triangle Applications
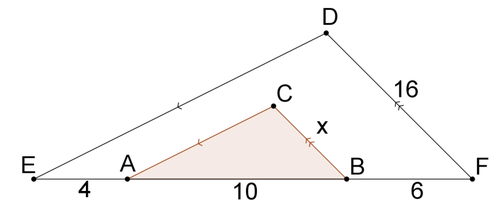
  ::类似三角三角应用

  播放段落

  Create similar triangles in order to solve for $\begin{align*}x\end{align*}$ .
  ::创建相似的三角形以解析 x 。

  

  播放段落

  Extend $\begin{align*}\overline{AD}\end{align*}$ and $\begin{align*}\overline{BC}\end{align*}$ to create point $\begin{align*}G\end{align*}$ .
  ::扩大和BC 创建G点。

    播放段落

  $\begin{align*}\triangle DGC\end{align*}$ $\begin{align*}\sim\end{align*}$ $\begin{align*}\triangle EGF\end{align*}$ $\begin{align*}\sim\end{align*}$ $\begin{align*}\triangle AGB\end{align*}$ by $\begin{align*}AA \sim\end{align*}$ because angles $\begin{align*}\angle DCG\end{align*}$ , $\begin{align*}\angle EFG\end{align*}$ , $\begin{align*}\angle ABG\end{align*}$ are all right angles and are therefore congruent and all triangles share $\begin{align*}\angle G\end{align*}$ . This means that their corresponding sides are proportional. First, solve for $\begin{align*}GC\end{align*}$ by looking at $\begin{align*}\triangle DGC\end{align*}$ and $\begin{align*}\triangle EGF.\end{align*}$   $\begin{align*}\triangle DGC \sim \triangle EGF\end{align*}$ which means that corresponding sides are proportional.
  ::由AAQO的DGCEGAGAGB, 因为角度 ZQDCG, EFG, ABG都是正对角度, 因此是相近的, 所有三角都分享了QG。 这意味着它们对应的一面是正比的。 首先, 通过查看 QDGC 和 QEGF, 解决GC 。 DGCEGF, 表示对应的一面是正比的 。

  播放段落

  Therefore:
  ::因此:

  播放段落

  $\begin{align*} \frac{DG}{EG}& = \frac{GC}{GF} = \frac{DC}{EF} \\ \frac{DC}{GC} & = \frac{EF}{GF} \vphantom{\Huge{X}}\\ \frac{2}{GC} &= \frac{3.5}{2.5 + GC}\vphantom{\Huge{X}}\\ 5 + 2GC &= 3.5 GC \vphantom{\huge{X}}\\ 5 &= 1.5 GC \\ GC & \approx \ 3.33 \end{align*}$
  ::DGEG=GCGF=DCEFDCGC=EFGFX2GC=3.52.5+GCX5+2GC=3.5GCX5=1.5GCGCGC3.33

  播放段落

  Next, solve for $\begin{align*}x\end{align*}$ by looking at $\begin{align*}\triangle DGC\end{align*}$ and $\begin{align*}\triangle AGB.\end{align*}$   $\begin{align*}\triangle DGC \sim \triangle AGB\end{align*}$ which means that corresponding sides are proportional.
  ::接下来,通过查看“DGC”和“AGB”来解答 x。“DGC”和“AGB。“DGC”意味着相应的两面是成比例的。

  播放段落

  Therefore:
  ::因此:

  播放段落

  $\begin{align*}\frac{DG}{AG} & = \frac{GC}{GB} = \frac{DC}{AB} \\ \frac{DC}{GC} & = \frac{AB}{GB} \vphantom{\Huge{X}}\\ \frac{2}{3.33} &= \frac{x}{1.5+2.5+3.33} \vphantom{\Huge{X}}\\ \frac{2}{3.33} &= \frac{x}{7.33} \vphantom{\Huge{X}}\\ x &= 4.4 \vphantom{\huge{X}} \end{align*}$
  ::DGAG=GCGB=DCABDCDCGC=ABGBX23.33=x1.5+2.5+3.333X23.33=x7.33Xx=4.4X

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Michael is 6 feet tall and is standing outside next to his younger sister. He notices that he can see both of their shadows and decides to measure each shadow. His shadow is 8 feet long and his sister's shadow is 5 feet long. How tall is Michael's sister?
  ::迈克尔身高6英尺,站在他妹妹的旁边。他注意到,他能看见他们的两个影子,并且决定测量每个阴影。他的影子长8英尺,妹妹的影子长5英尺。迈克尔的妹妹有多高?

  播放段落

  You can answer this question  by   applying what you know about  similar triangles.
  ::您可以应用您对相似三角形的了解来回答这个问题。

  播放段落

  The sun creates shadows at the same angle for both Michael and his sister. Assuming they are both standing up straight and making right angles with the ground, similar triangles are created.
  ::太阳为迈克尔和他妹妹以同样的角度创造阴影。 假设它们都站立直,用地面做右角度,就会产生相似的三角形。

  

  播放段落

  Corresponding sides are proportional because the triangles are similar.
  ::对应边是成比例的,因为三角形是相似的。

  播放段落

  $\begin{align*}\frac{\text{Michael's Height}}{\text{Sister's Height}} &= \frac{\text{Length of Michael's Shadow}}{\text{Length of Sister's Shadow}} \\ \frac{6 \ \text{ft}}{\text{Sister's Height}} &= \frac{8 \ \text{ft}}{5 \ \text{ft}} \\ \text{Sister's Height} & = \frac{6 \cdot 5}{8} \\ & = 3.75 \ \text{ft} \end{align*}$
  ::Michael's HeightSister's HeightSister's Height's Height's Height #迈克尔's Height's Height's Height's Height's Hight's Hight's Hight's Length 迈克尔's Height's Height's Height's Height's Height's Hight's length 迈克尔's ShowLength of sister's sister's show6's ft Sister's height=8 ft5 sister's height=658=3.75英尺

  播放段落

  His sister is 3.75 feet tall.
  ::他妹妹高3.75英尺

  播放段落

  Example 2
  ::例2

  播放段落

  Prove that all isosceles right triangles are similar.
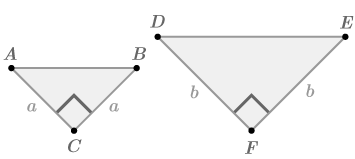
  ::证明右三角形的所有等分层都是相似的。

  播放段落

  Consider two generic isosceles right triangles:
  ::考虑两个通用的右等分形三角形 :

  

  播放段落

  Two pairs of sides are proportional with a ratio of $\begin{align*}\frac{b}{a}\end{align*}$ . Also, $\begin{align*}\angle C \cong \angle F\end{align*}$ . Therefore, the two triangles are similar by $\begin{align*}SAS \sim.\end{align*}$
  ::两对边与巴比成正比。同样,ZCQF。因此,两个三角与SASQ是相似的。

  播放段落

  Example 3
  ::例3

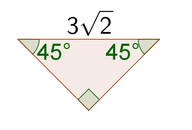
  播放段落

  Find the measures of the angles of an isosceles right triangle . Why are isosceles right triangles called 45-45-90 triangles?
  ::查找一个等离子体右三角形角度的度量。 为什么等离子体右三角形叫做 45 - 45 - 90 三角形?

  播放段落

  The base angles of an isosceles triangle are congruent. If the vertex angle is $\begin{align*}90^\circ \end{align*}$ , each base angle is $\begin{align*}\frac{180^\circ - 90^\circ}{2} = 45^\circ\end{align*}$ . The measures of the angles of an isosceles right triangle are 45, 45, and 90.
  ::等分三角形的基角是相同的。如果顶端角是 90 ,则每个基角是 180 90 2 = 45 。等分三角形右角的度量为 45、45 和 90。

  播放段落
  • An isosceles right triangle is called a 45-45-90 triangle because those are its angle measures.
    ::右三角的等离子体被称作 45 -45 -90 三角体, 因为这些是它的角度量。

    

  播放段落

  Example 4
  ::例4

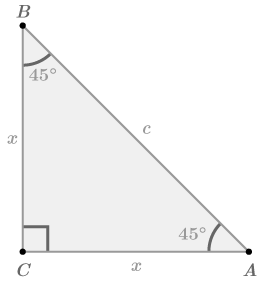
  播放段落

  Use the Pythagorean Theorem to find the missing side of an isosceles right triangle whose legs are each length $\begin{align*}x\end{align*}$ .
  ::使用 Pythagorean 理论来找到一个右三角形缺失的一面, 右三角形的腿每长x 。

  

  播放段落

  The missing side is the hypotenuse of the right triangle, labeled  $\begin{align*}c.\end{align*}$
  ::缺失的一面是右三角形的下方 标记为C

  播放段落

  By the Pythagorean Theorem,
  ::以毕达哥里安神话盟誓,

  播放段落

  $\begin{align*}AB^2 & = AC^2 + BC^2 \\ c^2 & = x^2 + x^2 \\ c^2 & = 2 x^2 \\ c & = \sqrt{2 x^2 } \\ c & = x \sqrt{2} \end{align*}$
  ::AB2=AC2+BC2c2=x2+x2c2=2x2c=2x2c=2x2c=x2c=x2c=x2c=x2c=x2c=x2c

  播放段落
  • The ratio of the sides of any isosceles right triangle will be $\begin{align*}\boldsymbol{x:x:x \sqrt{2}}\end{align*}$ which simplifies to $\begin{align*}\bf{1:1:\sqrt{2}}.\end{align*}$
    ::任何右三角等星边的比为x:x:x=2,该方形简化为1:#2。

  播放段落

  Example 5
  ::例5

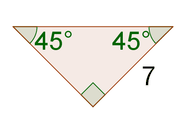
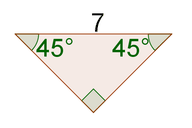
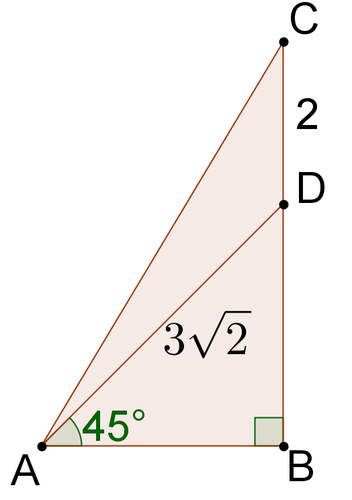
  播放段落

  F ind the missing sides of the right triangle below without using the Pythagorean Theorem.
  ::在不使用毕达哥伦神话的情况下 找到右三角形下面的缺失侧面

  

  播放段落

  If one of the legs is 3, then the other leg is also 3, so $\begin{align*}AC=3\end{align*}$ . The ratio of the sides of an isosceles right triangle is $\begin{align*}1:1:\sqrt{2}\end{align*}$ . Therefore, the hypotenuse will be $\begin{align*}3 \sqrt{2},\end{align*}$  so $\begin{align*}AB = 3 \sqrt{2}\end{align*}$ .
  ::如果其中一条腿是3条,另一条腿也是3条,那么AC=3。 右三角一等骨的两侧比例是1:#2。 因此,下限为32, 所以AB=32。

  Summary

  播放段落 Similar triangles have congruent corresponding angles and proportional corresponding sides. ::类似的三角形具有相近对应的角度和比例对应的两边。 播放段落 The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar. ::三角形相似性AA标准规定,如果两个三角形有两对相近角,三角形就相似。 播放段落 The SAS criterion for triangle similarity states that if two sides of one triangle are proportional to two sides of another triangle and their included angles are congruent, then the triangles are similar. ::关于三角相似性的SAS标准规定,如果一个三角的两面与另一个三角的两面成正比,而且其中的角是相同的,那么三角就是相似的。 播放段落 The SSS criterion for triangle similarity states that if three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar. ::三角形相似性SSS标准规定,如果一个三角形的三边与另一个三角形的三边成正比,那么三角形是相似的。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. Explain why all 30-60-90 triangles are similar.
  ::1. 解释为什么所有30-60-90三角都相似。

  播放段落

  2. The ratio between the sides of any 30-60-90 triangle is ________:________:________.
  ::2. 任何30-60-90三角形两侧的比率为_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Find the missing sides of each triangle:
  ::找到每个三角形的缺失边 :

  3.

  

  4.

  

  5.

  

  播放段落

  6. Explain why all 45-45-90 triangles are similar.
  ::6. 解释为什么所有45-45-90三角形都相似。

  播放段落

  7. The ratio between the sides of any 45-45-90 triangle is ________:________:________.
  ::7. 任何45-45-90三角形两侧之间的比率为________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Find the missing sides of each triangle:
  ::找到每个三角形的缺失边 :

  8.

  

  9.

  

  10.

  

  播放段落

  Use the figure below for #11 and #12.
  ::使用下图的 #11和#12。

  

  播放段落

  11. Prove that $\begin{align*}\triangle ABC \sim \triangle EFD\end{align*}$ .
  ::11. 证明ABC-EFD。

  播放段落

  12. Find the value of $\begin{align*}x\end{align*}$ .
  ::12. 查找x的值。

  播放段落

  Use the figure below for #13-#15.
  ::使用下图的 #13-#15。

  

  播放段落

  13. Find $\begin{align*}m \angle ADB\end{align*}$ . What type of triangle is $\begin{align*}\triangle ADB\end{align*}$ ?
  ::13) 找到亚银 哪一种三角形是亚银?

  播放段落

  14. Find $\begin{align*}BD\end{align*}$ and $\begin{align*}AB\end{align*}$ .
  ::14. 找到BD和AB。

  播放段落

  15. Find $\begin{align*}AC\end{align*}$ .
  ::15. 寻找AC。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。