7.1 更替比率-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节相近比率

  折叠 展开

  相近比率

  播放段落

  We know that two triangles are geometrically similar if they have two pairs of congruent angles.
  ::我们知道两个三角形的几何相似 如果它们有两对相似角度的话

  播放段落

  This means that two right triangles are similar if they have one (additional) pair of congruent angles .
  ::这意味着两个右三角如果有一个(额外)对齐角度, 则相似 。

  播放段落

  Since they are similar triangles, their corresponding sides are proportional. Knowing the sides are proportional means you can easily solve for the length of  an unknown  side  in one triangle just by multiplying the length of the corresponding side by the ratio of a given pair of corresponding sides.
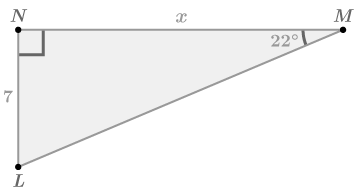
  ::由于它们相似的三角形, 它们对应的两边是成比例的。 了解两边是成比例的, 意味着一个三角形中未知的两边的长度很容易解决, 只需将对应的两边的长度乘以给定的两边的比。

  播放段落

  Consider the missing side $\begin{array}{r}x,\end{array}$  in the triangle below:
  ::考虑缺失的侧面 x, 在以下三角形中 :

  播放段落

  The two right triangles are similar because they have two pairs of congruent angles.
  ::两个右三角是相似的, 因为它们有两对相似的角度。

  播放段落

  Sides  $\begin{array}{r}\overline{DF}\end{array}$ and $\begin{array}{r}\overline{AC}\end{array}$ are corresponding because they are both opposite the $\begin{array}{r}{22}^{\circ }\end{array}$ angle.
  ::DF和AC是对应的 因为它们都在22号角对面

  播放段落

  The ratio of the two known side lengths is:  $\begin{array}{r}\frac{DF}{AC}=\frac{4}{2}=2\end{array}$ , so the scale factor between the two triangles is 2.
  ::两个已知侧边长度的比率是:DFAC=42=2,所以两个三角之间的比例系数是2。

  播放段落

  Th erefore   $\begin{array}{r}x=10\end{array}$ , because $\begin{array}{r}\frac{FE}{CB}=\frac{10}{5}=2\end{array}$ .
  ::因此x=10,因为FECB=105=2。

  ---

  播放段落

  The Tangent  Ratio
  ::相近比率

  播放段落

  In fact, t he ratio between the two legs of any $\begin{array}{r}{22}^{\circ }\end{array}$ right triangle will always be the same, because all $\begin{array}{r}{22}^{\circ }\end{array}$ right triangles are similar , since they all have the same angle measures.
  ::事实上,任何22右三角形的两腿之间的比例总是一样,因为所有22右三角形是相似的,因为它们都有相同的角度量。

  播放段落

  In a $\begin{array}{r}{22}^{\circ }\end{array}$  right triangle, t he ratio of the length of the leg opposite the $\begin{array}{r}{22}^{\circ }\end{array}$ angle to the length of the leg adjacent to the $\begin{array}{r}{22}^{\circ }\end{array}$ angle will always be $\begin{array}{r}\frac{2}{5}=0.4\end{array}$ . You can use this fact to find a missing side of another $\begin{array}{r}{22}^{\circ }\end{array}$  right triangle, which means it actually takes surprisingly little information to 'solve' a right triangle. 
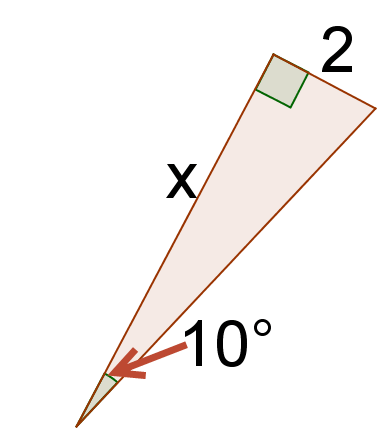
  ::在 22 右三角形中, 22 角对面的腿长度与 22 角对面的腿长度之比总是 25 = 0.4。 您可以使用这个事实来找到另一个 22 右三角形中缺失的一面, 这意味着“ 解决” 右三角形需要的信息少得惊人。

  播放段落

  1. What is the length of side $\begin{array}{r}x\end{array}$ ?
  ::1. 侧x的长度是多少?

    

  

  播放段落

  Because this is a $\begin{array}{r}{22}^{\circ }\end{array}$ right triangle, you know that $\begin{array}{r}\frac{\text{opposite leg}}{\text{adjacent leg}}=\frac{2}{5}=0.4\end{array}$ .
  ::因为这是一个22右三角形, 你知道对面的腿腿=25=0.4。

  播放段落

  F ollow the solution steps in the interactive image: 
  ::在交互式图像中遵循解决方案步骤 :

  播放段落

  The ratio between the opposite leg and the adjacent leg for a given angle in a right triangle is called the tangent ratio . Your scientific or graphing calculator has tangent programmed into it, so that you can determine the $\begin{array}{r}\frac{\text{opposite leg}}{\text{adjacent leg}}\end{array}$ ratio for any angle within a right triangle.
  ::在右三角形中,对立腿和相邻腿对一个角度的比被称为正切比。您的科学或图形计算器已经将正切率编入其中,以便您能够确定右三角形中任何角的对立腿比。

  播放段落

  The abbreviation for tangent is .
  ::相切缩略语缩略语是

  播放段落

  2. In the right triangle below, if angle $\begin{array}{r}C\end{array}$ is acute, find the value of $\begin{array}{r}\tan C\end{array}$ .
  ::2. 在下方右三角形,如果角C为急性,则找到TanC的价值。

  播放段落

  The value of $\begin{array}{r}\tan C\end{array}$ is .
  ::tanC的值是 。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  播放段落

  Tangent Graphs
  ::正切图

  ---

  播放段落

  Solving for Unknown Values
  ::解决未知值

  播放段落

  1. Solve for $\begin{array}{r}x\end{array}$ .
  ::1. 解决x.

  播放段落

  Use your calculator to find the tangent of $\begin{array}{r}{75}^{\circ }\end{array}$ .
  ::使用您的计算器查找 75 的正切值 。

  播放段落

  Make sure your calculator is in degree mode. Then, type " $\begin{array}{r}\tan (75)\end{array}$ ".
  ::确保您的计算器在度模式中。 然后, 输入“ tan( 75) ” 。

  播放段落

  $\begin{array}{r}\tan ({75}^{\circ })\approx 3.732\end{array}$
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ~ ~~ ~ ~ ~~ ~~ ~~ ~ ~~ ~~ ~ ~~ ~~~ ~~ ~~ ~ ~~ ~

  播放段落

  This means that the ratio of the length of the opposite leg to the length of the adjacent leg for a $\begin{array}{r}{75}^{\circ }\end{array}$ angle within a right triangle will be approximately 3.732.
  ::这意味着右三角内75角的对立腿长度与相邻腿长度之比将约为3.732。

  播放段落

  Now y ou know that the ratio $\begin{array}{r}\frac{\text{opposite leg}}{\text{adjacent leg}}\approx 3.732\end{array}$ . You can use this to solve for $\begin{array}{r}x:\end{array}$
  ::现在你知道对立腿的比数=3.732。 您可以用这个来解答 x:

  播放段落

  2. Solve for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ .
  ::2. 解决x和y。

  

  播放段落

  You can use the $\begin{array}{r}{65}^{\circ }\end{array}$ angle to find the correct ratio between 24 and $\begin{array}{r}x\end{array}$ . 
  ::您可以使用65角来找到24和x之间的正确比例。

  播放段落

  Note that this answer is only approximate because you rounded the value of $\begin{array}{r}\tan {65}^{\circ }.\end{array}$  An exact answer will include " $\begin{array}{r}\tan \end{array}$ ". The exact answer is:
  ::请注意,这个答案只是粗略的,因为您四舍五入了 tan\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  $$\begin{array}{r}x=\frac{24}{\tan {65}^{\circ }}\end{array}$$

  
  ::x=24tan65

  播放段落

  To solve for $\begin{array}{r}y\end{array}$ , use :  
  ::要解决y, 请使用 :

  ---

  播放段落

  Tangent Ratio
  ::相近比率

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle $\begin{array}{r}ABC\end{array}$ and observe how the tangent ratio of $\begin{array}{r}\mathrm{\angle }A\end{array}$ and $\begin{array}{r}\mathrm{\angle }B\end{array}$ changes.
  ::单击下方图像旁边的小蓝箭头,然后拖动橙色顶部以重塑三角 ABC 并观察 A 和 B 的正切比是如何变化的。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  As the measure of an angle increases between $\begin{array}{r}{0}^{\circ }\end{array}$ and $\begin{array}{r}{90}^{\circ },\end{array}$  how does the tangent ratio of the angle change?
  ::当角度值在 0 和 90 之间增加时, 角的正切比是如何变化的 ?

  播放段落

  As an angle increases, the length of its opposite leg increases. Therefore, $\begin{array}{r}\frac{\text{opposite leg}}{\text{adjacent leg}}\end{array}$ increases and thus the value of the tangent ratio increases.
  ::随着角度的增加,其相反腿的长度会增加。 因此,相邻腿的对面腿会增加,因此相切比的价值也会增加。

  播放段落

  Example 2
  ::例2

  播放段落

  Tangent tells you the ratio of the two legs of a right triangle with a given angle. Why does the tangent ratio not work in the same way for non-right triangles?
  ::Tangent 告诉您右三角的两腿与给定角度的比。 为什么正切比对非右三角不以同样方式工作?

  播放段落

  Two right triangles with a $\begin{array}{r}{32}^{\circ }\end{array}$ angle will be similar. Two non-right triangles with a $\begin{array}{r}{32}^{\circ }\end{array}$ angle will not necessarily be similar. The tangent ratio works for right triangles because all right triangles with a given angle are similar. The tangent ratio doesn't work in the same way for non-right triangles because not all non-right triangles with a given angle are similar.
  ::带有 32 角的两个右三角将相似。 两个带有 32 角的非右三角不一定相似。 正切比对右三角有效, 因为所有带有指定角的右三角都相似。 正切比对非右三角不同样有效, 因为不是所有带有指定角的非右三角都相似 。

  播放段落

  You can only use the tangent ratio for right triangles.
  ::您只能使用右三角形的正切比 。

  播放段落

  Example 3
  ::例3

  播放段落

  Use your calculator to find the tangent of $\begin{array}{r}{45}^{\circ }.\end{array}$  What does this value represent?  Present an argument for why this value makes sense.
  ::使用您的计算器查找 45 的正切值。 这个值代表什么 ? 为为什么这个值有意义提供一个参数 。

  播放段落

  Using a calculator:   $\begin{array}{r}\tan ({45}^{\circ })=1\end{array}$  
  ::使用计算器: tan( 45)=1

  播放段落

  This means that the ratio of the length of the opposite leg to the length of the adjacent leg is equal to 1 for right triangles with a $\begin{array}{r}{45}^{\circ }\end{array}$  angle.
  ::这意味着对面腿长度与相邻腿长度之比,45角的右三角形等于1。

  播放段落

  This should make sense because right triangles with a $\begin{array}{r}{45}^{\circ }\end{array}$  angle are isosceles. The legs of an isosceles triangle are congruent , so the ratio between them will be 1.
  ::这应该有道理, 因为右三角形的角为 45 角是等分数。 等分三角形的腿是相容的, 所以它们之间的比值将是 1 。

  播放段落

  Example 4
  ::例4

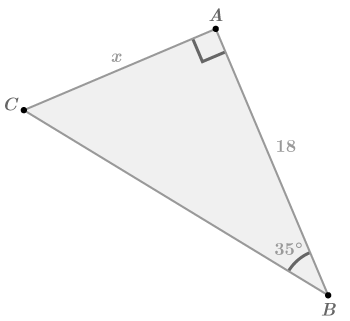
  播放段落

  Solve for $\begin{array}{r}x\end{array}$ .
  ::解决x。

  

  播放段落

  Use the tangent ratio of a $\begin{array}{r}{35}^{\circ }\end{array}$  angle.
  ::使用角为 35 的正切比 。

  播放段落

  $\begin{array}{rl}\tan ({35}^{\circ })& =\frac{\text{opposite leg}}{\text{adjacent leg}}\\ \tan ({35}^{\circ })& =\frac{AC}{AB}=\frac{x}{18}\phantom{\underset{X}{\overset{X}{\sum }}}\\ x& =18\tan ({35}^{\circ })\\ x& \approx 18(0.7)\\ x& \approx 12.604\end{array}$
  ::~ (35) =对面的团团团团团团团团(35) =ACU=x18XXx=18tan(35)x1818(0.7)x12.604

  Summary

  播放段落 Two right triangles are similar if they have one (additional) pair of congruent angles ::两个右三角形相似,如果它们有一个(附加的)一对相似角度 播放段落 $\begin{array}{r}\tan (\theta )=\frac{\text{opp}}{\text{adj}}\end{array}$ ::tan =oppadj

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. Why are all right triangles with a $\begin{array}{r}{40}^{\circ }\end{array}$  angle similar? What does this have to do with the tangent ratio?
  ::1. 为什么直角为40的三角形都相似?这与正切比有什么关系?

  播放段落

  For questions 2 through 7, round your answers to the nearest hundredths place.
  ::问题2至问题7,请在最接近的一百个地方 翻转你的答案

  播放段落

  2. Find the tangent of $\begin{array}{r}{40}^{\circ }.\end{array}$
  ::2. 找出40的正切值。

  播放段落

  3. Solve for $\begin{array}{r}x\end{array}$ .
  ::3. 解决x.

  

  播放段落

  4. Find the tangent of $\begin{array}{r}{80}^{\circ }.\end{array}$
  ::4. 找出80元的正切值。

  播放段落

  5. Solve for $\begin{array}{r}x\end{array}$ .
  ::5. 解决x.

  

  播放段落

  6. Find the tangent of $\begin{array}{r}{10}^{\circ }.\end{array}$
  ::6. 找出10元的相切值。

  播放段落

  7. Solve for $\begin{array}{r}x\end{array}$ .
  ::7. 解决x.

  

  播放段落

  8. Your answer to #5 should be the same as your answer to #7. Why?
  ::8. 你对5号的回答应该和你对7号的回答相同 为什么?

  播放段落

  For questions 9 through 13, round your answers to the nearest hundredths place.
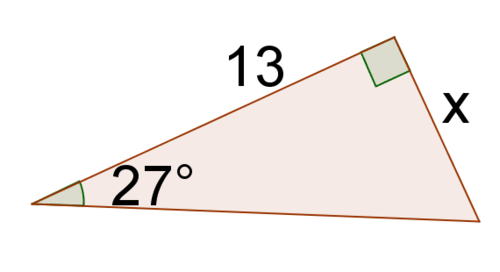
  ::问题9至13 请将答案转至最近的一百个地方

  播放段落

  9. Find the tangent of $\begin{array}{r}{27}^{\circ }.\end{array}$
  ::9. 找出相切的27。

  播放段落

  10. Solve for $\begin{array}{r}x\end{array}$ .
  ::10. 解决x.

  

  播放段落

  11. Find the tangent of $\begin{array}{r}{42}^{\circ }.\end{array}$
  ::11. 找出42的相切值。

  播放段落

  12. Solve for $\begin{array}{r}x\end{array}$ .
  ::12. 解决x.

  

  播放段落

  13. A right triangle has a $\begin{array}{r}{42}^{\circ }\end{array}$  angle. The base of the triangle, adjacent to the $\begin{array}{r}{42}^{\circ }\end{array}$  angle, is 5 inches. Find the area of the triangle.
  ::13. 右三角有42角。三角形的底部与42角相邻,为5英寸。找到三角形的区域。

  播放段落

  14. Recall that the ratios between the sides of a 30-60-90 triangle are $\begin{array}{r}1:\sqrt{3}:2\end{array}$ . Find the tangent of $\begin{array}{r}{30}^{\circ }.\end{array}$  Explain how this matches the ratios for a 30-60-90 triangle.
  ::14. 回顾30-60-90三角形两侧的比率为1:3:2, 找出30- 30的正切值。 请解释这与 30- 60- 90 三角形的比率如何匹配 。

  播放段落

  15.  Describe why you think the value of the tangent ratio increases as the angle goes from $\begin{array}{r}{0}^{\circ }\end{array}$  to $\begin{array}{r}{90}^{\circ }.\end{array}$  Defend your answer.
  ::15. 说明为什么你认为角值从0升至90时,正切比的值会增加。

  播放段落

  16. Kaci is building a bike ramp for jumps. She wants the angle of elevation of the ramp with respect to the ground to be $\begin{array}{r}{30}^{\circ }.\end{array}$  What is the slope of her ramp? What are some reasonable dimensions for the ramp that will have this slope?
  ::16. Kaci正在建造一个自行车坡道,以便跳跃,她希望坡道的高度角是30°C。她的坡道的斜坡是多少?斜坡的合理的尺寸是什么?

  播放段落

  17. Theo and Kaci are debating. Theo thinks that the slope of the line below is $\begin{array}{r}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}\end{array}$ while Kaci thinks it's $\begin{array}{r}\tan \theta .\end{array}$  Who is correct and why?
  ::17. Theo和Kaci正在辩论,Theo认为下线的斜坡是x,而Kaci认为是。

  

  播放段落

  18. Why is tangent defined as opposite over adjacent instead of the other way around?
  ::18. 为什么对正切点的定义是相对的,而不是相反?

  播放段落

  19. The following diagram shows Theo and Kaci are standing 5 kilometers away from each other, watching a balloon ascending between them. The angle of elevation from Kaci to the balloon is  $\begin{array}{r}{30}^{\circ }.\end{array}$  The angle of elevation from Theo to the balloon is $\begin{array}{r}{60}^{\circ }.\end{array}$ How high is the balloon? Round your answer to the nearest thousandths place.
  ::19. 下图显示Theo和Kaci相互距离距离5公里,看着气球在它们之间升起,从Kaci升到气球的角是30°C,从Theo升到气球的角是60°C。气球的高度是多高?将答案绕到最近的一千个地方。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。