8.8 到圆圈的清空线-interactive
章节大纲
-
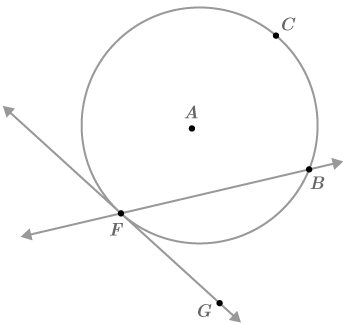
Recall that a line that intersects a circle in exactly one point is called a tangent line . A line that intersects a circle in two points is called a secant line . Secant means 'to cut' extracted from a Latin word 'secare'. In a circle, a secant will touch the circle in exactly two points and a chord is the line segment defined by these two points. Below, is a secant.
::回顾在一点中将圆交错的一条线被称作正切线。在两点中将圆交错的一条线被称作松动线。从拉丁词“secare”中抽取的“切开”意指“切开”。在一个圆中,一个松动将用精确的两个点触碰圆,而一个和弦是这两个点定义的线段。下面, AB是松动线段。When two secants or a tangent and a secant are drawn, they can interact in four ways. In each case, arcs, angles and line segments have special relationships. These ideas are summarized below, and will be explored further and proved in the examples and practice.
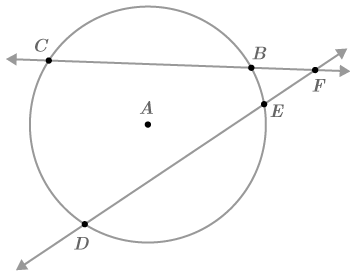
::当画出两个割裂或切线和割断时,它们可以以四种方式相互作用,每一种情况下,弧、角和线段都有特殊的关系,这些想法概述如下,并将在实例和实践中进一步探讨和证明。Case #1: Two secants intersect outside the circle.
::案例1:两个分离体在圆外交叉。Relevant Theorems:
::相关理论:-
(This will be explored in #1 below)
::BFCF=EFDF(将在下文#1中探讨) -
(This will be explored in #2 below)
::mCDmBE2=mBFE(将在下面#2中探讨)
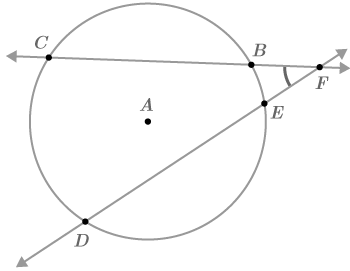
Case #2 : Two secants intersect inside the circle.
::案例2: 圆圈内有2个分离体交叉。Relevant Theorems:
::相关理论:-
(This was previously proved as a property of intersecting chords)
::CF°FB=DFEFE(这以前被证明是交叉和弦的属性) -
(This will be explored in #3 below)
::mCDmBE2=mBFE=mCFD(将在下面第3号中探讨)
Case #3 : A secant and a tangent intersect on the circle.
::案例3: 圆形上的割裂和相切交叉。Relevant Theorem :
::相关定理 :-
(This will be explored in Example 1)
::MBBG=MBF #2(将在例1中加以探讨)
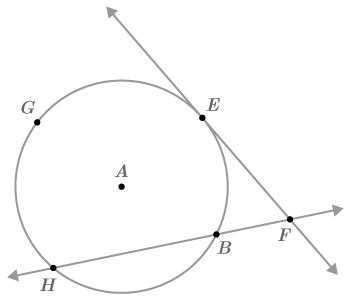
Case #4 : A secant and a tangent intersect outside the circle.
::案例4:圆外的割裂和相切交叉。Relevant Theorems:
::相关理论:-
::FBFH=FE2 -
::mHGE= mGE= mGE=mGE=mGE=mBE=mBFE= mHGE=mGE=mGE=mGE=mBE=mBFE=mBFE=mBFE=mBFE=mGE=mGE=mBFE=mBFE=mBFE=mBFE=mBE=mBFE=mBFE=mGE=mGE=mGE=mBFE=mBFE=mBFE=mBFE=mBFE=mBFE=m=mBFE=mBFE=mBFE=mBFE=mBFE=M =MGE=MGE=MGE= mGE= mGE=mBE=BE=BE=BFE=BFE=M =MBF =BFE=M =MBFE=BF =M=M=BF =BFE =M =M =M =BFE =M =M=BFE =BFE =M =B =B =M =M =M =B =B =B =B = = =B = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
CK-12 PLIX: Tangent Secant Theorem
::CK-12 PLIX: 唐氏定理Let's take a look at some problems involving secant lines.
::让我们来研究一下 与松散线有关的一些问题1. Prove that .
::1. 证明BFCF=EFDF。Draw chords and .
::画和弦CE和DBTwo triangles are created, and . Note that both triangles share . Also note that both and are inscribed angles of . Therefore, . Because and have two pairs of congruent angles, they are similar by . This means that corresponding sides of the triangles are proportional. In particular, . This means that .
::创建了两个三角, CEF 和 DBF 。 请注意, BCE 和 EDB 是 BEQ 的刻入角度。 因此, BCE EEEDB 。 因为 CEF 和 DBF 有两对相近角度, AAQ 相似。 这意味着三角的对应边是成比例的。 特别是 BFEF= DFCF。 这意味着 BFACF = EFDF 。 这意味着 BFCF= EFDF 。2. Prove that .
::2. 证明MCD=mBE=mBFE。You are trying to prove that the measure of the angle is equal to half the difference between the measures of the red arc and the blue arc. As in #1, draw chords and .
::您试图证明角度的测量等于 红弧和蓝弧的测量值的 一半。 如 # 1, 绘制和弦 CE 和 DB 。Consider how the angles and arcs are related.
::考虑角度和弧之间的关系。-
(inscribed angle)
::mCED=mCD%2( 说明角度) -
(inscribed angle)
::mECF=mBE%2( 说明角度) -
(
exterior angle
equals the sum of the remote interior angles)
::mCED=mECF+mBFE(外角等于远程内角之和)
Make two substitutions and you have:
::做两个替代,你有:
::mCD2=mBE2+mBFETherefore,
::因此,mBFE=mCD2-mBE2=mCD=mBE23. Prove that .
::3. 证明MCD=mBE=mBFE=mCFD。This logic of this proof is similar to the logic used in #2. Start by drawing chord .
::这个证据的逻辑与#2中的逻辑相似。 从绘制和弦 DB开始。Consider how the angles and arcs are related.
::考虑角度和弧之间的关系。-
(inscribed angle)
::mCBD=mCD%2( 指定角度) -
(inscribed angle)
::mBDE=mBE2(说明角) -
(exterior angle equals the sum of the remote interior angles)
::mCFD=mCBD+mBDE(外角等于边远内角之和)
Make two substitutions and you have:
::做两个替代,你有:
::mCFD=mCD=2+mBE=2Therefore, . Because and are , they are congruent and have equal measures. This means .
::因此, mCD=mBE2=mCFD。因为 & & CFD 和 {BFE} 具有相似性, 具有同等措施。 这意味着 mCD=mBE2=mBFE=mCFD 。
Examples
::实例实例实例实例Example 1
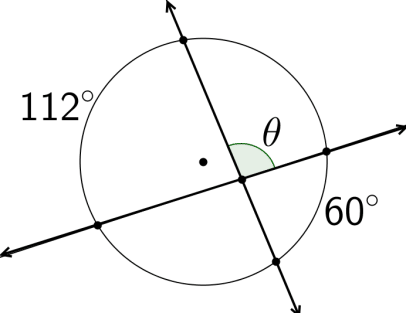
::例1In the circle below, , , and . Find .
::在下面的圆形中, mCD100, mBC120, 和 mDE100. find mBFE.This is an example of two secants intersecting outside the circle. The intersection angle of the two secants is equal to half the difference between their intercepted arcs. In other words, . You are given , but you don't know . Use the fact that a full circle is to find .
::这是圆外两个分离体交叉的一个例子。 两个分离体的交叉角等于被截取弧之间的一半差。 换句话说, mBFE=mCDmBE2。 您得到了 mCD100, 但是您不知道 mBE。 使用一个全圆是360 来找到 mBE 。
::mB*360*mCD*mBC*mDE*mBE*mB*mCD*mBC*mDE*
::mB*%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @Now, solve for the measure of .
::现在,解决测量ZBFE。
::mBFE=mCD=mBE=2mBFE=100+40=2mBFE=30Example 2
::例2is tangent to circle at point . Prove that .
::F. 证明 mBFG=mbF2Draw a diameter through points and . This segment will be perpendicular to .
::通过 F 点和 A 点绘制直径。 此段将直径与 FG Q 垂直 。First note that because the two arcs make a semicircle . This means that and thus .
::第一注, mCBmbF180, 因为这两个弧形成半圆圈。 这意味着 mCB2+mBF2=90, 因此 mBF2=90mCB2。Now consider other angle and arc relationships:
::现在考虑其他角度和弧关系 :-
(inscribed angle)
::mCFB=mCB2(引角) -
(two angles make a right angle)
::mCFB+mBFG=90(两个角度右角)
By substitution, .
::以 mCB2+mBFG=90代替。Therefore, .
::因此,MBFG=90°mCB_2。Consider the two highlighted statements. Both and are equal to . Therefore, .
::MBF2和MZBFG均等于90兆CB2,因此,MZBFG=MBF2。Example 3
::例3. Find .
::mFCB280. 找到 mBFG.If , then . Therefore, .
::如果mFCB=280,那么mFB=36036028080。因此,mBFG=mbF=2=802=40。Example 4
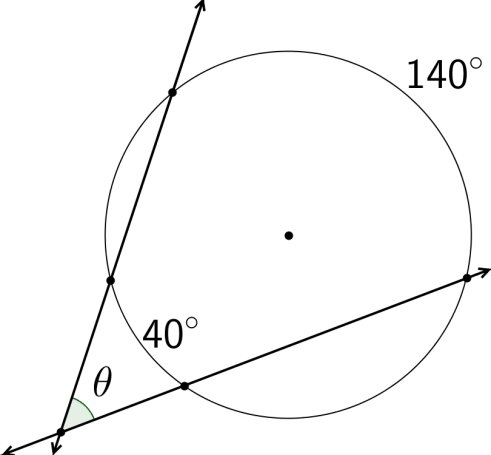
::例4and . Find .
::mCD70和 mBE40 找到MCFEand . is the average of the measure of the intercepted arcs.
::mCD70和 mBE40.mCFD是被拦截弧的平均值。
::-==============================================================================================================================================================================================================================================55==============================================================================================================================================================================================================================================================================Therefore,
::因此,.
::MCFE=180 mCFD=180 555 125 *CFDM=180 *CFDM*CFE=180 *55 *125*。Summary -
A
secant line
is a line that intersects a circle in two points.
::秒线是将圆交错为两点的线。 -
A
chord
is a line segment whose endpoints are on a circle.
::和弦是一条线段,端点在圆上。 -
The
tangent secant theorem
states if a tangent and a secant are drawn from a common point outside the circle, then
::相切的偏差定理表示从圆外的一个共同点抽出正切和偏差, 然后 a2=b(b+c) 。
Review
::审查审查审查审查1. What's the difference between a secant and a tangent?
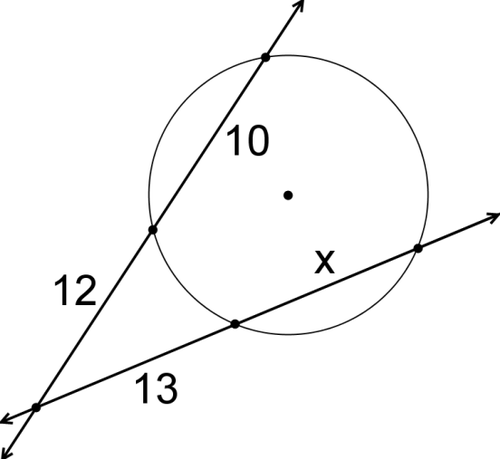
::1. 分离和相切之间有什么区别?For questions #2 through #7 round your answer to the nearest tenths place. Use the relationships explored in this concept to solve for or in each circle.
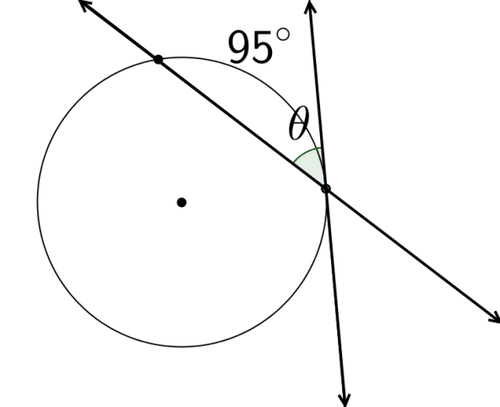
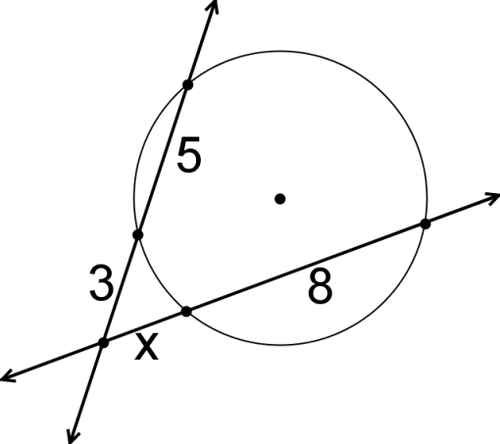
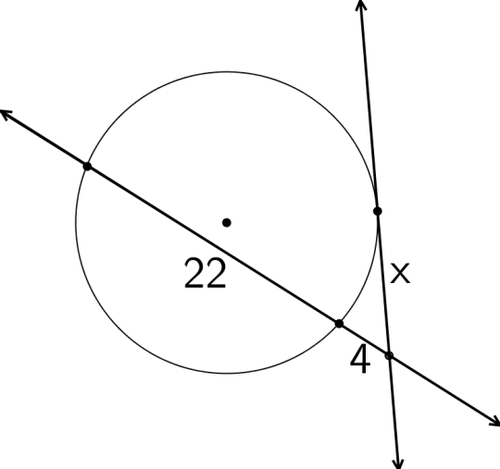
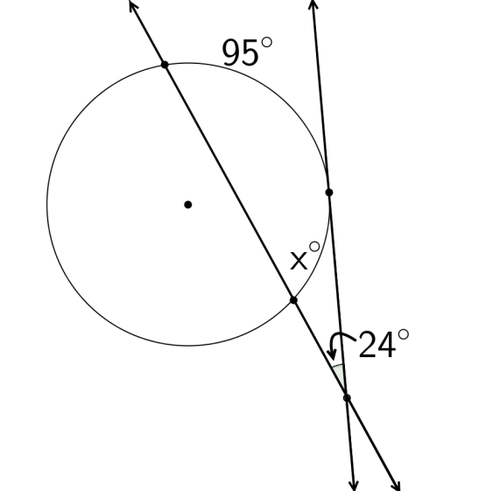
::对于问题# 2 到 # 7, 您对最近的十分位的答案回合为 # 2 到 # 7 。 使用此概念中探讨的关系来解决每个圆圈中的 x 或 。2.
3.
4.
5.
6.
7.
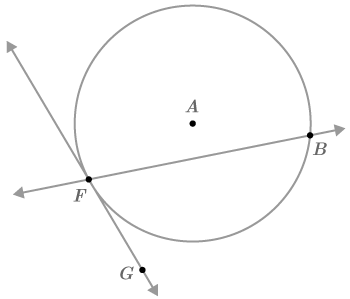
In #8-#12 you will explore Case #4: A secant and a tangent intersect outside the circle.
::在#8-#12中,你将探索4号案例:圆圈外的片断和相切交叉。8. Assume forms a diameter. Draw in the diagram diameter and chord . Explain why
::8. 假设他直径直径,在图表直径上画出他和弦的弦。解释为什么“FEB'EHB”是“FEB'EHB”的原因。9. Prove that
::9. 证明FHEZEFEB10. Prove that
::10. 证明FB-FH=FE211. Prove that (Use Example B to help).
::11. 证明 mHGE2=mBE2+mBFE(使用例B帮助)。12. Prove that
::12. 证明MHGE=MHGE=MBE=MHGE=MBFE13. How is the theorem proved in questions #11 and #12 related to the theorem proved in Examples 2?
::13. 在例2中与理论相关的问题11和12中,如何证明理论理论得到证实?Solve for or in each circle.
::每个圆圈的 x 或 。14.
15.
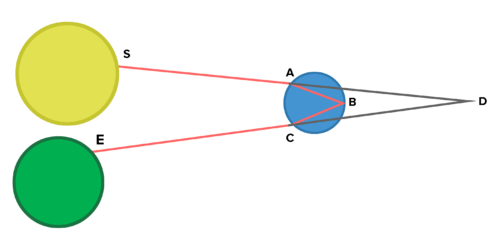
16. Rainbows are created when droplets of water bend (or refract) the sunlight as it passes through them. The different angles of refraction give different wavelengths of light to make the rainbow. Look at the figure below:
::16. 彩虹是当水弯(或折射)的液滴通过阳光时产生的,反射的不同角度给予不同波长的光来制作彩虹。Light from the sun leaves point S and travels through the air and reaches a drop of water at point A, where it bends. The light goes to the back of the drop of water (point B) and it is reflected to then move out of the drop of water at C. From here the light heads to earth (point E). In the diagram point D shows how much this ray of light has deviated from its original path. Explain how you could calculate the angle at point D.
::阳光从太阳离开S点处亮出, 穿过空气, 到达它弯曲的A点一滴水。 光向水滴的背面( B点) , 然后从C点的水滴中移动。 从这里光头到地球( E点)。 图表点D 显示这一束光与最初路径有多么不同。 解释您如何计算 D点的角 。17. In the famous movies attributed to Star Trek, there is a specific logo considered to be the Starfleet Insignia. Research this logo and use your knowledge of circles and secants to describe it in words. Can you find another logo that uses the properties of secants?
::17. 在《星际迷航》的著名电影中,有一个特定的标志被认为是星际舰队徽章,研究这个标志,并利用你对圆圈和空档的了解用文字来描述它。你能找到另一个使用空档特性的标志吗?Review (Answers)
::审查(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
(This will be explored in #1 below)