课程： 9.5 三维建模-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

三维建模

Warm-Up
::暖热

Geometric shapes can be modeled with equations and 2- dimensional pictures. Use the interactive below, to explore connections between a 2- dimensional and a 3- dimensional box. Later in this section, you will use equations with variables to solve real world problems that use 2 and 3-dimensional objects.
::几何形状可以用方程和二维图片建模。使用下面的交互效果, 来探索二维和三维框之间的联系。在此区域稍后部分, 您将使用带有变量的方程来解决使用二维和三维天体的现实世界问题。

Modeling in Three Dimensions
::三维建模

You live in a three dimensional world. Look around and observe what you see over the course of your day. Can you find examples of prisms? Cylinders? Pyramids ? Cones? Spheres?
::你生活在一个三维的世界里。看看周围,观察你今天所看到的。你能找到棱镜的例子吗? 圆柱形? 金字塔? 锥形? 锥形? 球形? 球形?

While most objects in your daily life are not perfect prisms, pyramids, cylinders, cones, or spheres . M ost are close to one of these five solids or a combination of these solids. Modeling in three dimensions is about being able to choose the best solid to help analyze a real world three dimensional situation, and then using your geometry knowledge to make decisions about the real life situation. You should ask yourself:
::虽然你日常生活中的大多数物体都不是完美的棱镜、金字塔、圆柱、锥形或球体。多数物体接近于这5个固体中的1个或这些固体的组合。模拟三个维是能够选择最好的固体来帮助分析真实世界的三维状况,然后利用你的几何学知识来决定真实生活状况。您应该问自己:

What solid or solids are the best model of this real life object?
::什么样的固态或固态是这个真实生命物体的最佳模型?

What problems am I trying to solve or decisions am I trying to make about the real life object?
::我试图解决什么问题或决定我试图做出什么关于真实的物体?

What information about the real life object am I given and where does it fit in my model?
::我给的关于真实生命物体的信息是什么? 它适合我的模型吗?

Real-World Application: Chopping Trees
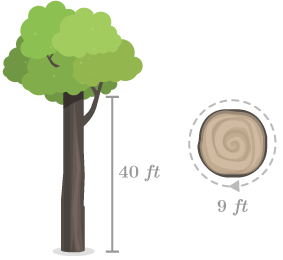
::真实世界应用程序:购物树

A big storm causes a large tree to fall in your yard. The main portion of the tree trunk measures about 9 feet around and is 40 feet long. You plan to chop up the tree to use and sell as fire wood. Approximately what of wood will you get from the tree?
::大风暴使一棵大树倒在你的院子里。树干干的主要部分大约在9英尺左右,长40英尺。你打算砍树,把树当作木柴出售。你从树上取出木柴的多少?

A tree trunk, 40 feet tall and 9 feet in circumference, shown with a cross-section.

A tree trunk is best modeled by a cylinder . Here, you are looking for the approximate volume of the cylinder. Two pieces of information are given.
::树干最好用气瓶做模型。这里, 您正在寻找气瓶的大致体积。给出了两部分信息。

1. "The main portion of the tree trunk measures about 9 feet around" - This is the of the base of the cylinder. You can use this measurement to find the radius of the cylinder.
::1. “树干主干部分测量周围9英尺左右” - 这是圆柱的底部, 您可以使用此测量找到圆柱的半径。

$\begin{aligned} C & = 2 π r \\ r & = \frac{C}{2 π} = \frac{9}{2 π} \\ r & \approx 1.43 ft \end{aligned}$
::C=2rr=C292r1.43英尺

2. "40 feet long" - This is the height of the cylinder.
::2. "40英尺长" - 这是气瓶的高度

$\begin{aligned} h = 40 ft \end{aligned}$
::h=40英尺

The volume of the wood from the tree is approximately:
::树上木柴的体积约为:

$\begin{aligned} V = π r^{2} h = π (1.43)^{2} (40) \approx 257 {ft}^{3} \end{aligned}$
::Vr2h(1. 432(40)257英尺

Real-World Application: Buying Wood
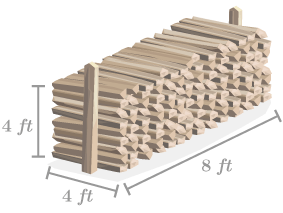
::真实世界应用程序:购买木柴

Wood is commonly sold in cords. A cord of wood is a stack of tightly packed wood that measures 4 feet by 4 feet by 8 feet. Approximately how many cords of wood will the chopped tree from the first problem produce?
::木柴通常是用绳索出售的。木柴的一根绳子是一串紧凑的木柴,用4英尺乘4英尺乘4英尺乘8英尺。从第一个问题开始,砍断的木柴大约会产生多少条木柴?

A stack of firewood measuring 4 feet by 4 feet by 8 feet, representing one cord.

A cord of wood is best modeled by a rectangular prism . $\begin{aligned} V_{prism} = A_{base} \cdot h \end{aligned}$ , so $\begin{aligned} V = (4 \cdot 4) \cdot 8 = 128 {ft}^{3} . \end{aligned}$ Each cord of wood is approximately 128 cubic feet of wood. Since the tree from the first problem produced 257 cubic feet of wood, this is $\begin{aligned} \frac{257}{128} \approx 2 \end{aligned}$ cords of wood.
::木条的最佳模型是长方形棱柱。 Vprism=Abaseh, 所以V=( 44)8=128平方英尺。每根木条大约是128立方英尺的木。由于第一个问题产生的树木为257立方英尺的木,因此,这是257128+2根木条。

Now, let's come up with an equation that relates the length around a tree in feet, the height of a tree in feet, and the approximate number of cords of wood that a tree will produce.
::现在,让我们想出一个方程式, 将一棵树的足长,一棵树的脚高, 以及一棵树将生产的木柴的大致数量联系起来。

You want to come up with an equation that takes an input of circumference and height and produces an output of cords of wood. Think back to the steps given in guidance and repeat these steps with variables for circumference and height instead of specific values.
::您想要找到一个方程, 该方程可以输入环形和高度, 并生成木质线的输出。回想在制导中给定的步骤, 并重复这些步骤, 使用环形和高度变量而不是特定值。

Let $\begin{aligned} C = \end{aligned}$ distance around the tree
::C=在树周围的距离

Let $\begin{aligned} h = \end{aligned}$ height of tree
::Let h=树高

Use the distance around the tree to find the radius:
::使用树周围的距离查找半径 :

$\begin{aligned} C = 2 π r \to r = \frac{C}{2 π} \end{aligned}$
::C=2rr=C2

Once you have the volume of the wood from a given tree, to find the number of cords of wood divide the volume by $\begin{aligned} 128 {ft}^{3} \end{aligned}$ , which is the number of cubic feet in a cord of wood.
::一旦找到一棵树的木头数量, 就会发现木头的绳索数量将体积除以128 平方英尺, 也就是木根的立方英尺数量。

$\begin{aligned} Number of Cords = \frac{V}{128} = \frac{\frac{C^{2} h}{4 π}}{128} = \frac{C^{2} h}{512 π} \end{aligned}$
::数=V128=C2h4128=C2h512

Test this formula using the original information from the first problem about chopping trees to see if you get the correct answer to the second problem. In this first problem, $\begin{aligned} C = 9 ft \end{aligned}$ and $\begin{aligned} h = 40 ft . \end{aligned}$
::测试此公式时, 使用从砍树的第一个问题中获得的原始信息的原始信息来测试第二个问题是否得到正确的答案。在此第一个问题中, C=9 ft 和 h=40 ft 。

$\begin{aligned} Number of Cords = \frac{C^{2} h}{512 π} = \frac{(9)^{2} (40)}{512 π} \approx 2.01 \end{aligned}$
::Cords=C2h512(9)2(402(40)5122.01

This matches the answer you found the first time, so you can feel confident that your equation is correct.
::这个答案与你第一次找到的答案吻合, 这样你就能确信你的方程式是正确的。

Examples
::实例实例实例实例

Example 1
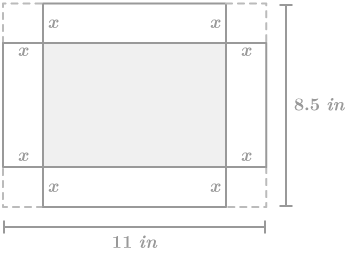
::例1

Mark wants to make an open box from an 8.5 inch by 11 inch piece of paper by cutting squares out of each corner, folding up the sides, and securing with tape. How does the volume of the box relate to the size of the squares he cuts out?
::马克想要用8.5英寸乘11英寸的纸从每个角落切开方形,折叠两边,用磁带固定,从一个8.5英寸乘11英寸的纸块上做一个打开的盒子。盒子的体积与他切开的方形大小有何关系?

Let the length of the side of the square that Mark cuts out of each corner be $\begin{aligned} x . \end{aligned}$ The portion of the paper that will become the base of the box once it is made is shaded below in gray.
::让马克从每个角切开的方形侧面的长度 x。纸制成后将成为盒子底部的部分在下面灰色阴影下。

Dimensions of an 8.5x11 inch paper showing cut squares at corners for box volume calculation.

The box is a rectangular prism. The volume of the box is therefore $\begin{aligned} V = A_{base} \cdot h . \end{aligned}$
::框是一个矩形棱柱。因此,框的体积是 V=Abaseh。

$\begin{aligned} A_{base} = (11 - 2 x) (8.5 - 2 x) = 4 x^{2} - 39 x + 93.5 \end{aligned}$
::基准=(11-2x)(8.5-2x)=4x2-39x+93.5

$\begin{aligned} h = x \end{aligned}$
::h=xx 小时=x

Therefore, the volume of the box in terms of the size of the square is:
::因此,按方形大小计算,框的体积如下:

$\begin{aligned} V = x (4 x^{2} - 39 x + 93.5) = 4 x^{3} - 39 x^{2} + 93.5 x \end{aligned}$
::V=x(4x2-39x+93.5)=4x3-39x2+93.5x

Mark can use this formula to determine the volume of the box given the length of the side of the squares he cuts out. For example, if he cuts out squares that are 2 inch by 2 inch, then $\begin{aligned} x = 2. \end{aligned}$ The volume of the box would be:
::马克可以使用此公式来根据他切开的方形的长度来决定框的体积。例如,如果他切开的方形为2英寸乘以2英寸,那么 x=2。框的体积将是:

$\begin{aligned} V = 4 (2)^{3} - 39 (2)^{2} + 93.5 (2) = 63 {in}^{3} \end{aligned}$
::V=4(2)3-39(2)(2)2+93.5(2)=63英寸3

Example 2
::例2

Graph the equation $\begin{aligned} y = 4 x^{3} - 39 x^{2} + 93.5 x \end{aligned}$ , derived in Example #1, with a graphing calculator. What do the points on this graph represent? What portion of this graph is relevant to this problem?
::图形 y= 4x3- 39x2+93.5x 方程式, 由例1 中导出, 带有图形计算器。此图上的点代表什么? 此图的哪个部分与此问题相关 ?

The points on the graph represent the volume of the box given the length of the side of each square cut out.
::图形上的点数代表框的体积,以切除的每个方形的侧面长度为准。

Because Mark can't cut out a square with a negative side length or a square with a side length greater than 4.25 inches (because the paper is only 8.5 inches wide), the portion of the graph that is relevant is the portion with $\begin{aligned} x \end{aligned}$ values between 0 and 4.25 .
::因为马克无法切除负侧长的正方形或长大于4.25英寸的正方形(因为纸张宽度只有8.5英寸),图中相关的部分是X值介于0至4.25之间的部分。

Example 3
::例3

Approximately what size squares will maximize the volume of the box (cause the box to have the greatest possible volume)? How does the graph above help you to answer this question?
::大约哪个大小的方形将最大化框的体积( 因为框的体积最大) ? 上图如何帮助您回答这个问题 ?

The maximum volume looks to occur with squares that are approximately 1.6 inches by 1.6 inches. The volume at that point looks to be around $\begin{aligned} 66 {in}^{3} \end{aligned}$ . The graph helps to answer this question because the peak on the graph is where the maximum volume occurs.
::最大体积的方形大约为1.6英寸乘1.6英寸。当点的体积大约为66英寸。图形有助于回答这个问题, 因为图形上的峰值是最大体积的所在地。

Example 4
::例4

Does the size of square that maximizes volume also maximize of the box? Explain.
::使体积最大化的平方大小是否也使框体积最大化? 解释。

The surface area of the open box will be the area of the unfolded box (the net). The more you cut out of the paper, the smaller the surface area. Therefore, the size of square that maximizes volume does not also maximize surface area of the box.
::开口框的表面区域将是展开框的区域( 网)。您从纸上剪出的面积越大, 表面面积越小。因此, 最大体积的平方的大小, 也不使框的表面面积最大化。

Because Mark can't cut out a square with a negative side length or a square with a side length greater than 4.25 inches (because the paper is only 8.5 inches wide), the portion of the graph that is relevant is the portion with $\begin{aligned} x \end{aligned}$ values between 0 and 4.25.
::因为马克无法切除负侧长的正方形或长大于4.25英寸的正方形(因为纸张宽度只有8.5英寸),图中相关的部分是X值介于0至4.25之间的部分。

CK-12 PLIX: Absolute Extrema and Optimization
::CK-12 PLIX: 绝对极端和优化

Discussion Question
::讨论问题

Try unfolding a cereal box. What is the surface area and volume of the box? What changes would you make to the cut-outs of the net to maximize the volume of the box?
::尝试显示一个麦片盒。盒子的表面面积和体积是多少? 您对网的切除会做出什么改变来使盒子的体积最大化 ?

Summary

A net is a diagram that shows a “flattened” or unfolded representation of a solid. In a net, each face and base is shown with all of its dimensions. A net can also serve as a pattern to build a three-dimensional solid.
::网是一个显示固态“ 缩放” 或展开的表示图。在网中,每个面孔和基底都显示其所有维度。网也可以作为构建三维固态的模式。

You can use the equation and graph that represents the volume of a shape with variables to solve optimization problems.
::您可以使用方程式和图形来表示形状的大小,其中含有变量,以解决优化问题。

Review
::审查审查审查审查

An 11 inch tall roll of paper towels has an inner cardboard tube with a diameter of 1.5 inches. The width of the paper towel on the roll is 2 inches and each paper towel is 0.015 inches thick.
::11英寸高的纸毛巾有内纸板管,直径1.5英寸,卷纸毛巾宽2英寸,每条纸毛巾厚0.015英寸。

1. What is the volume of paper towels? Will the volume change if the roll of paper towels is unrolled?
::1. 纸巾的数量是多少?如果纸巾卷开,纸巾卷会改变吗?

2. If the whole roll of paper towels is unrolled, how long will the chain of unrolled paper towels be? [Hint: Use your answer to #1 to help]
::2. 如果整卷纸毛巾被拆开,那连串的纸毛巾还要花多长时间? [提示:用你对#1的回答来帮助]

3. Come up with an equation that generalizes the relationship between the variables: diameter of tube, width of paper towel on roll, thickness of paper towel, and length of unrolled paper towels. Why does the height of the paper towel roll not matter in this relationship?
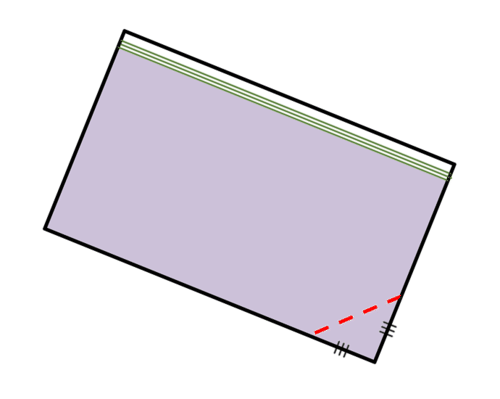
::3. 提出一个概括变数之间关系的方程式:管直径、滚动纸巾宽度、纸巾厚度和无滚动纸巾长度,为什么纸巾卷的高度在这种关系中无关紧要?

In order to decorate a cake with purple frosting, Sam plans to fill a zipper sandwich bag with frosting, cut off one of the tips of the bag, and squeeze the frosting out of the corner (see picture below).
::为了装饰一个带有紫霜的蛋糕,Sam计划用霜冻填满一个拉链三明治包,切掉一个袋子的小指头,并将霜冻挤出角落(见下图)。

4. Assuming he cuts an isosceles triangle out of the corner, what length of cut should he make to pipe frosting with a 1 centimeter diameter. In other words, what should the length of the red dotted line be?
::4. 假设他将一个等分形三角形从角切开,他应该用什么长度来截断直径为1厘米的结霜管,换句话说,红点线的长度应该有多大?

5. Give an equation that shows the relationship between the length of the cut made and the diameter of the frosting as it comes out of the bag.
::5. 给出一个方程式,显示切割长度与从包里出来时霜冻直径之间的关系。

6. You are packing up yearbooks that measure 11 inches by 14 inches by 1.5 inches. You have boxes that measure 12 inches by 30 inches by 10 inches. How many books can you fit in each box?
::6. 包装年刊,以11英寸乘14英寸乘1.5英寸。箱内有12英寸乘30英寸乘10英寸。每个箱内有多少本书?

A certain burning candle loses $\begin{aligned} 7 {in}^{3} \end{aligned}$ of volume each hour.
::某种燃烧的蜡烛每小时损失7英寸3的体积。

7. If the original candle was 10 inches tall with a diameter of 3 inches, what is the volume of the candle after 3 hours?
::7. 如果最初的蜡烛是10英寸高,直径为3英寸,3小时后蜡烛的体积是多少?

8. Create an equation that relates the original height of the candle, the diameter of the candle, the time burned, and the current volume of the candle for all candles that lose $\begin{aligned} 7 {in}^{3} \end{aligned}$ of volume per hour.
::8. 建立一个方程式,将蜡烛最初的高度、蜡烛的直径、燃烧的时间和目前所有蜡烛的蜡烛体积联系起来,每小时蜡烛体积减少7英寸3。

9. Mike and his friends are having a water balloon fight. Each approximately spherical balloon can hold one cup of water. If one cup of water has a volume of approximately $\begin{aligned} 14.44 {in}^{3}, \end{aligned}$ what is the radius of each filled balloon?
::9. 迈克和他的朋友在争水气球,每个球球球球都可举一杯水,如果每杯水的体积约为14.44英寸,每瓶气球的半径大约是14.44英寸,则每个装满气球的半径是多少?

Marissa works at an ice cream shop. The sugar cones have a diameter of 2 inches and a height of 4 inches. For a single scoop cone, she packs the cone with ice cream and then puts a scoop on top. For a double scoop cone, she packs the cone with ice cream and then puts two scoops on top (see sketch below). For a triple scoop cone, she packs the cone with ice cream and then puts three scoops on top. One cup of ice cream has a volume of $\begin{aligned} 14.44 {in}^{3} . \end{aligned}$
::玛丽莎在一家冰淇淋店工作。糖锥直径为2英寸,高度为4英寸。她用冰淇淋把锥子打包,然后把勺子放在顶部。对于双球锥, 她用冰淇淋把锥子打包, 然后把两勺子放在顶部(见下面的草图 ) 。对于三勺锥, 她用冰淇淋把锥打包, 然后把三勺子放在顶部。一杯冰淇淋在3英寸内有14.44分。一杯冰淇淋在3英寸内有14.44分。

10. Approximately how much ice cream (in cups) does a single scoop cone get?
::10. 大约一个单勺锥形冰淇淋(杯中)能得到多少?

11. Approximately how much ice cream (in cups) does a double scoop cone get?
::11. 双勺锥形冰淇淋(在杯子里)大约能得到多少冰淇淋?

12. Approximately how much ice cream (in cups) does a triple scoop cone get?
::12. 三勺圆锥冰淇淋(在杯子里)能得到多少?

13. Describe at least two reasons why your answers to the previous three questions are only approximate.
::13. 请至少说明贵国对前三个问题的答复为何只是近似原因。

14. If a single scoop cone costs $2.50 and a double scoop cone costs $3.50. Which type of cone is a better deal considering cost per cup of ice cream?
::14. 如果一个独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独独独独独独独独独独独独独独独独独家独家独家独家独家独家独家独家独家独家独家独家独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独独

15. If a single scoop cone costs $2.50, what should a triple scoop cone cost if it is fairly priced?
::15. 如果一个独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独承办公司的独家独承办公司的独家独家独家独承办公司的独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独家独

16. Consider the cone within the sphere below. The sphere has a radius of 1. Two possible configurations for the cone are shown. The base of the cone is always a circle on the sphere. Imagine changing $\begin{aligned} ∠ D A C \end{aligned}$ such that the cone gets taller and thinner, or shorter and fatter. What measure of $\begin{aligned} ∠ D A C \end{aligned}$ maximizes the volume of the cone? Create an equation for the volume of the cone as a function of the angle. What range of values for the angle are acceptable in this scenario? Graph this function using a graphing calculator, and approximate the maximum. Sketch the result.
::16. 将锥体在下面的球体中考虑锥体。球体的半径为 1 。显示锥体的两种可能的配置。锥体的底部始终是球体上的圆圈。想象一下正在变化的-DAC,让锥体变高,变瘦,或变矮,变胖。什么是-DAC,使锥体的体积最大化?创造锥体体体体积的方程式,作为角的函数。在这种假设中,角体的值范围是多少?用图形计算器绘制这个函数,并接近最大值。结果可以绘制。

Review (Answers)
::审查(答复)

To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.
::要查看本书的答案键, 请在“ ” 选项下点击答案键。

章节大纲

常规

三维建模

Warm-Up ::暖热

Modeling in Three Dimensions ::三维建模

Real-World Application: Chopping Trees ::真实世界应用程序:购物树

Real-World Application: Buying Wood ::真实世界应用程序:购买木柴

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX: Absolute Extrema and Optimization ::CK-12 PLIX: 绝对极端和优化

Discussion Question ::讨论问题

Review ::审查审查审查审查

Review (Answers) ::审查(答复)