Course: 10.3 Parabolas等同-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

百万分数平方

Consider a point and a line. Can you think of a new point whose distance from the original point is also equal to the distance of the line?
::考虑一个点和一条线。你能想到一个新点, 与原点的距离也等于线的距离吗 ?

Grid showing a point above a dashed horizontal line, illustrating distance concepts for parabolas.

Now, consider all the points that are the same distance away from the point as the line. Can you imagine what the set of ALL the points would look like? Use the PLIX Interactive to demonstrate this scenario.
::现在, 请考虑所有与线条距离相同的点。您能想象所有点的组合会是什么样子吗 ? 使用 PLIX 互动来演示这个情景。

CK-12 PLIX: Parabolas
::CK-12 PLIX: 帕拉波拉斯

The set of all points the same distance from a given point and a line is a parabola .
::与给定点相同的距离的所有点组和一条线是抛物线。

In the past you thought of a parabola in terms of its vertex and intercepts. Another way of defining a parabola is as the set of points that are equidistant from a point called the focus and a line called the directrix . This alternate way of thinking about a parabola leads to another general equation for :

For parabolas opening up or down with a horizontal directrix: $\begin{align*}(x-h)^2=4p(y-k) \end{align*}$
::使用水平直方向x-h)2=4p(y-k)

For parabolas opening left or right with a vertical directrix: $\begin{align*}(y-k)^2=4p(x-h)\end{align*}$
::使用垂直直轴(y-k)2=4p(x-h)打开左面或右面的parabolas

In each case, $\begin{align*}(h, k) \end{align*}$ is the vertex of the parabola. $\begin{align*}p\end{align*}$ is the distance from the vertex to the focus (and also the distance from the vertex to the directrix).
::在每种情况下,(h,k)是抛物线的顶点。 p是从顶点到焦点的距离(还有从顶点到直线的距离)。

To derive the general equation for the parabola, pick a generic point on a parabola and find an equation that shows the relationship between the distance from that point to the focus and the distance from that point to the directrix.
::为了得出抛物线的一般方程,在抛物线上选择一个通用点,并找到一个表明从该点到焦点的距离和从该点到直线的距离之间关系的方程。

Deriving the Equation of a Parabola
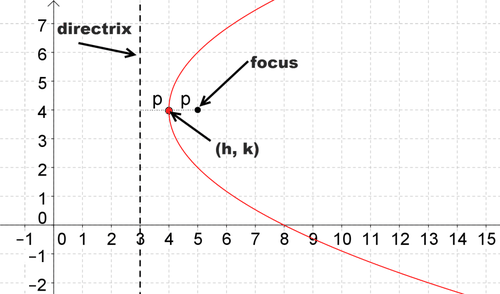
::推导帕拉波拉的等同

1. Consider the parabola below. The vertex is at $\begin{align*}(h, k) \end{align*}$ and at a distance of $\begin{align*}p\end{align*}$ from the focus .
::1. 考虑下面的抛物线。顶点在(h,k)处,距离焦点距离(p)。

If we only consider parabolas that open upwards or downwards, then the directrix will be a horizontal line of the form $\begin{align*}y = c\end{align*}$ . Because the directrix is also a distance of $\begin{align*}p\end{align*}$ from the vertex , it must be at height $\begin{align*}k-p\end{align*}$ . The equation of the directrix is $\begin{align*}y=k-p\end{align*}$ .
::如果我们只考虑向上或向下打开的parabolas, 直线将是表y=c的一条水平线。因为直线也是p与顶点的距离, 它必须是在k-p高度。直线的方程式是 y=k-p 。

The focus has the same $\begin{align*}x\end{align*}$ -coordinate as the vertex and has a height that is $\begin{align*}p\end{align*}$ more than the height of the vertex. The focus is at $\begin{align*}(h, k+p)\end{align*}$ .
::焦点与顶点具有相同的x坐标,其高度比顶点的高度高。焦点在(h,k+p)处。

2. Consider a random point $\begin{align*}(x, y) \end{align*}$ on the parabola connected to the focus with a right triangle .
::2. 考虑用右三角形连接焦点的抛物线上的随机点(x,y)。

Find the distance from the point to the focus using .
::查找从点点到焦点的距离,使用。

The two legs of the triangle are $\begin{align*}x-h \end{align*}$ and $\begin{align*}y-(k+p)\end{align*}$ . The distance from the focus to the point is the hypotenuse of the triangle, $\begin{align*}c\end{align*}$ .
::三角形的两条腿是 x-h 和 y- (k+p) 。从焦点到点的距离是三角形的下限, c 。

$\begin{align*}& (x-h)^2+(y-(k+p))^2=c^2 \\ & c=\sqrt{(x-h)^2+(y-(k+p))^2} \end{align*}$
:x-h)2+(y-(k+p))2=c2c=(x-h)2+(y-(k+p))2

Therefore, the distance from the point to the focus is $\begin{align*}\sqrt{(x-h)^2+(y-(k+p))^2}\end{align*}$ .
::因此,从点到焦点的距离是(x-h)2+(y-(k+p))2。

Identify the directrix in the given figure.
::在给定数字中指定直线。

The directrix in the given figure is .
::给定数字中的准点是 .

The distance from the point to the directrix is $\begin{align*}y-(k-p)\end{align*}$ .
::从点到准点的距离是y-(k-p)。

You are assuming that the random point $\begin{align*}(x, y)\end{align*}$ is on the parabola, and therefore it must be the same distance from the focus as from the directrix. This means that the two distances must be equivalent.
::您假设随机点( x,y) 是在抛物线上, 因此它与焦点的距离必须和直线的距离相同。这意味着这两个距离必须是相等的。

$\begin{align*}\sqrt{(x-h)^2+(y-(k+p))^2}=y-(k-p)\end{align*}$
:x-h)2+(y-(k+p))2=y-(k-p)

Your job is to simplify and algebraically manipulate this equation to show that it is equivalent to $\begin{align*}(x-h)^2=4p(y-k)\end{align*}$ . Start by squaring both sides of the equation, then expand all of the terms involving $\begin{align*}y\end{align*}$ , $\begin{align*}k\end{align*}$ and $\begin{align*}p\end{align*}$ , then simplify.
::您的工作是简化和代数操控此方程式, 以显示它相当于 (x- h) 2=4p(y- k) 。开始对方程式的两侧进行方块分隔, 然后扩展所有涉及 y、 k 和 p 的术语, 然后简化。

This is the equation of the parabola because the set of points on the parabola (which are the set of points that are the same distance from the focus as from the directrix), are the set of points that will satisfy this equation.
::这是抛物线的方程,因为抛物线上的一组点(即与焦点的距离与直线的距离相同的一组点)是符合这一方程的一组点。

Parabola
::帕拉波拉

Click the small blue arrow next to the image below.
::单击下方图像旁边的小蓝箭头。

Drag the focus (point $\begin{align*}F\end{align*}$ ) to see how it affects the shape of the parabola and its equation.
::拖曳焦点( F点) 以观察它如何影响抛物线的形状及其方程式。

Drag point $\begin{align*}A\end{align*}$ which will move the directrix line up and down, to see how it affects the shape of the parabola and its equation.
::拖点 A 将直线线向上和向下移动, 以观察它如何影响抛物线及其方程的形状。

Drag the point $\begin{align*}P\end{align*}$ on the parabola and observe the distance $\begin{align*}d\end{align*}$ from the focus to the curve is always the same as the distance from the point $\begin{align*}P\end{align*}$ to the directrix.
::拖动抛物线上的P点并观察从焦点到曲线的距离 d 总是与从P点到直线的距离相同。

Examples
::实例实例实例实例

Example 1
::例1

How does the shape of a parabola change as its focus and directrix move further apart?
::抛物线的形状如何随着其焦点和导线而变化?

As the distance increases between the focus and directrix, the parabola opens wider.
::随着焦点和准点之间的距离增加,抛物线打开的范围更广。

Example 2
::例2

Sketch the parabola $\begin{align*}(x-2)^2=4(y-5) \end{align*}$ using the vertex, focus and directrix.
::使用顶部、焦点和指向来对抛物线(x-2)2=4(y-5)进行折射。

The vertex is at $\begin{align*}(2,5)\end{align*}$ and $\begin{align*}p\end{align*}$ is 1. Plot the vertex and then find the focus and directrix. Finally, sketch in the parabola.
::顶点在 2 , 5 , p 1 。绘制顶点, 然后找到焦点和指针。最后, 草图在 parbola 中。

Example 3
::例3

Sketch the parabola $\begin{align*}(x-2)^2=-4(y-5)\end{align*}$ using the vertex, focus and directrix. What does it mean to have a negative value for $\begin{align*}p\end{align*}$ ?
::使用顶点、焦点和直线来折射抛物线(x-2)2 4 (y-5) 。负值对 p意味着什么 ?

A negative value for $\begin{align*}p\end{align*}$ means that the directrix is above the focus and the parabola opens down. The vertex is in the same place, but the focus and directrix switch places.
::p 的负值表示直线矩在焦点之上, 抛物线会打开。顶点在同一个地方, 但焦点和直线键开关的位置却相同。

Example 4
::例4

What is the equation of the parabola with focus $\begin{align*}(6,1)\end{align*}$ and directrix $\begin{align*}x=2\end{align*}$ ?
::抛物线与焦点(6,1)和指向x=2的等式是什么?

This parabola opens to the right. The vertex is in the middle of the focus and directrix, so the vertex is at $\begin{align*}(4,1)\end{align*}$ . $\begin{align*}p\end{align*}$ is 2. The equation is:
::此抛物线向右打开。顶点在焦点和指向的中间, 因此顶点在( 4, 1) 上, p是 2 。等式是 :

$\begin{align*}(y-1)^2=8(x-4)\end{align*}$
:y-1)2=8(x-4)

Summary

A parabola is the set of points in a plane that are equidistant from both the directrix (a fixed straight line) and the focus (a fixed point). The standard form of a parabola with center $\begin{align*}(h,k)\end{align*}$ and $\begin{align*}p\end{align*}$ distance from the focus:

$\begin{aligned} (x - h)^{2} = 4 p (y - k) \end{aligned}$
$\begin{align*}(x-h)^2=4p(y-k)\end{align*}$
::抛物线是指在直线(固定直线)和焦点(固定点)之间等距的平面上的一组点。抛物线是中(h,k)和偏距(p)的抛物线的标准形式x-h)2=4p(y-k)

Parabolas opening up or down with a horizontal directrix: $\begin{align*}(x-h)^2=4p(y-k)\end{align*}$
::Parabolas 以水平直线向上或向下打开或向下打开x-h)2=4p(y-k)

Parabolas opening left or right with a vertical directrix: $\begin{align*}(y-k)^2=4p(x-h)\end{align*}$
::Parabolas 以垂直直线向左或向右打开y-k)2=4p(x-h)

Review
::审查审查审查审查

1. What is the relationship between a parabola and its focus and directrix?
::1. 抛物线及其重点和准点之间的关系是什么?

For each equation below, state whether the parabola will open up, down, left, or right.
::对于以下的每一个方程式,请说明抛物线是向上、向下、向左还是向右打开的。

2. $\begin{align*}(x-4)^2=8(y+1)\end{align*}$
::2. (x-4)2=8(y+1)

3. $\begin{align*}(y+1)^2=-8(x-4)\end{align*}$
::3. (y+1)28(x-4)

4. $\begin{align*}(x-4)^2=-8(y+1)\end{align*}$
::4. (x-4)28(y+1)

5. $\begin{align*}(y+1)^2=8(x-4)\end{align*}$
::5. (y+1)2=8(x-4)

Sketch each parabola using its vertex, focus, and directrix.
::利用脊椎、焦点和指向将每个抛物线都涂抹在背面上

6. $\begin{align*}(x-4)^2=8(y+1)\end{align*}$
::6. (x-4)2=8(y+1)

7. $\begin{align*} (y+1)^2=-8(x-4)\end{align*}$
:y+1)28(x-4)

8. $\begin{align*}(x-4)^2=-8(y+1)\end{align*}$
::8. (x-4)28(y+1)

9. $\begin{align*}(y+1)^2=8(x-4)\end{align*}$
::9. (y+1)2=8(x-4)

10. What is the equation of the parabola with focus (4, 1) and directrix $\begin{align*} y=-3\end{align*}$ ?
::10. 抛物线与重点(4,1)和指针 y 3等式是什么?

11. What is the equation of the parabola with focus (3, 3) and directrix $\begin{align*}y=-5\end{align*}$ ?
::11. 抛物线与重点(3,3)和指针 y 5等式是什么?

12. What is the equation of the parabola with focus (2, 4) and directrix $\begin{align*}x=4\end{align*}$ ?
::12. 抛物线与焦点(2、4)和准点x=4的等式是什么?

Consider the sideways parabola below.
::考虑一下下面的侧道抛物线

13. What is the equation of the focus and the equation of the directrix in terms of $\begin{align*}h\end{align*}$ , $\begin{align*}k\end{align*}$ , and $\begin{align*}p\end{align*}$ ?
::13. 从h、k和p方面看,焦点的方程式和准点的方程式是什么?

14. Consider a random point $\begin{align*}(x, y)\end{align*}$ on the parabola. Find the distance from the point to the focus (see Example B for help).
::14. 考虑抛物线上的随机点(x,y),找出从点到焦点的距离(帮助请参见例B)。

15. Consider the same random point $\begin{align*}(x, y)\end{align*}$ on the parabola as in #14. Find the perpendicular distance from the point to the directrix.
::15. 考虑抛物线上的随机点(x,y)与第14号中的点相同。

16. Use your answers to #14 and #15 to derive the equation for the sideways parabola: $\begin{align*}(y-k)^2=4p(x-h)\end{align*}$ .
::16. 使用对#14和#15的回答来得出侧路抛物线的方程y-k)2=4p(x-h)。

17. Explain a way in which you can distinguish the equation of the parabola from the equation of a hyperbola.
::17. 请解释您如何区分抛物线的方程和双倍波拉的方程。

18. What is the relationship between the vertex, focus, directrix, and the axis of symmetry in a parabola?
::18. 抛物线的顶端、焦点、直线和对称轴之间的关系是什么?

19. You are given the standard form of the equation of a parabola. You know the vertex but do not know the value of $\begin{align*}p,\end{align*}$ the distance from the vertex to the directrix. What happens to the shape of parabola as the value of $\begin{align*}p\end{align*}$ gets larger? Wha t if the value of $\begin{align*}p\end{align*}$ gets smaller? Explain.
::19. 您获得了抛物线方程的标准形式。您知道顶点, 但不知道p的值, 顶点与直线之间的距离。抛物线的形状会变成 p 更大的? 如果 p 值变小, 会发生什么 ? 请解释。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

百万分数平方

CK-12 PLIX: Parabolas ::CK-12 PLIX: 帕拉波拉斯

Deriving the Equation of a Parabola ::推导帕拉波拉的等同

Parabola ::帕拉波拉

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::审查审查审查审查

Review (Answers) ::审查(答复)