课程： 10.5 距离公式-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

距离公式

When working on a coordinate plane , you can always find the distance between two points (or the length of a line segment) by creating a right triangle and using the Pythagorean Theorem .

For example, suppose you want to find the length of $\begin{aligned} \bar{A B} \end{aligned}$ .
::例如,假设你想找到AB的长度。

Draw a right triangle such that $\begin{aligned} \bar{A B} \end{aligned}$ is the hypotenuse .
::绘制右三角形,使AB为下限。

You can find the lengths of $\begin{aligned} \bar{B C} \end{aligned}$ and $\begin{aligned} \bar{A C} \end{aligned}$ by counting because they are vertical and horizontal line segments.
::您可以通过计数找到 BC 和 AC 的长度, 因为它们是垂直和水平线段。

Use the Pythagorean Theorem to find the length of $\begin{aligned} \bar{A B} \end{aligned}$ .
::利用毕达哥里理论来找到AB的长度。

$\begin{aligned} A B^{2} & = B C^{2} + A C^{2} \\ A B^{2} & = 2^{2} + 4^{2} \\ A B & = \sqrt{20} = 2 \sqrt{5} units \end{aligned}$
::AB2=BC2+AC2AB2=22+42AB=20=25 单位

Notice that $\begin{aligned} A B = \sqrt{B C^{2} + A C^{2}} \end{aligned}$ . This generalizes to a formula known as the distance formula. The distance formula states that the distance between $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ is $\begin{aligned} \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$ .
::注意 AB= BC2+AC2. 这一般化为称为距离公式的公式。距离公式表示( X1, y1) 和( X2, y2) 之间的距离是 (x2 - x1) 2+(y2 - y1) 2。

With the help of the distance formula, you can find the perimeter of polygons on a coordinate plane by finding the sum of the lengths of all the sides. You can also find the area of polygons by finding the lengths of key line segments like bases and heights.
::借助距离公式的帮助,您可以在坐标平面上找到多边形的周界,通过找到所有边的长度总和。您也可以通过找到基准和高度等关键线段的长度,找到多边形区域。

Use the Pythagorean Theorem to show that the distance between the two points below is $\begin{aligned} \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$ .
::使用 Pytagorean 理论来显示以下两点之间的距离是 (x2- x1) 2+ (y2-y1) 2。

Draw in a right triangle . The lengths of the legs are $\begin{aligned} (x_{2} - x_{1}) \end{aligned}$ and $\begin{aligned} (y_{2} - y_{1}) \end{aligned}$ . For now, let the length of the hypotenuse of the triangle (the distance you are trying to find) be " $\begin{aligned} k \end{aligned}$ ".
::在右三角形中绘制。腿的长度是 (x2- x1) 和 (y2- y1) 。目前, 三角形的下拉值长度( 您正在寻找的距离) 应该是 K 。

By the Pythagorean Theorem, $\begin{aligned} (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} = k^{2} \end{aligned}$ . Therefore, $\begin{aligned} k = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$ . The distance between the two points is $\begin{aligned} \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$ .
::by the Pythagorean Theorem, (x2-x1)2+(y2-y1)2+(y2-y1)2=k2. 因此, k=(x2-x1)2+(y2-y1)2+(y2-y1)2. 两点之间的距离是(x2-x1)2+(y2-y1)2。

What is the distance between point $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ ?
::A点和B点之间的距离是多少?

The distance between point $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ is .
::A点和B点之间的距离是。

Finding Perimeter Using Distance Formula
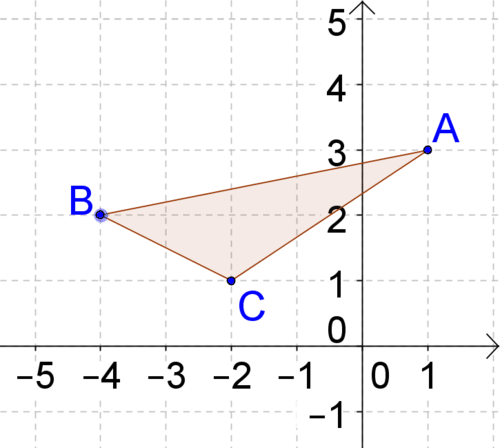
::使用远程公式查找周边

Let's consider a triangle $\begin{aligned} A B C \end{aligned}$ , whose perimeter you need to find.
::让我们考虑一个三角ABC, 其周界你需要找到。

Graph showing triangle ABC with vertices at points A, B, and C in a coordinate plane.

Use the distance formula to find the length of each side.
::使用距离公式查找每侧的长度。

The perimeter of the triangle is the distance around the triangle, which is the sum of the lengths of the three sides. The perimeter is
::三角形的周边是三角形周围的距离,这是三边长度的总和。

$\begin{aligned} A B \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} B C \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} A C \end{aligned}$ $\begin{aligned} = \sqrt{13} + \sqrt{5} + 2 \sqrt{5} = \sqrt{13} + 3 \sqrt{5} \approx 10.31 \end{aligned}$ units.
::AB+BC+AC=13+5+25=13+35+10.31单位。

Find the distance between $\begin{aligned} (2, 7) \end{aligned}$ and $\begin{aligned} (- 1, 5) \end{aligned}$ .
::查找(2,7)和(-1,5)之间的距离。

You can use the distance formula without plotting the points. Let $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ $\begin{aligned} = (2, 7) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) = (- 1, 5) \end{aligned}$ .
::您可以在不绘制点的情况下使用距离公式。 Let (x1,y1) = (2,7) 和 (x2,y2) = (-1,5) 。

$\begin{aligned} Distance = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} = \sqrt{(- 1 - 2)^{2} + (5 - 7)^{2}} = \sqrt{(- 3)^{2} + (- 2)^{2}} = \sqrt{9 + 4} = \sqrt{13} units \end{aligned}$
::距离=(x2-x1)2+(y2-y1)2+(y2-y1)2=(-1-2)2+(5-7)2=(-3)2+(-2)2+(-2)2=9+4=13单位

Note that it doesn't matter which point you choose for $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ . You could have also calculated the distance the other way, with $\begin{aligned} (x_{1}, y_{1}) = (- 1, 5) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) = (2, 7) \end{aligned}$ :
::请注意,您选择哪个点( x1,y1) 并不重要, 您也可以用( x1, y1) = (- 1, 5) 和 (x2, y2) = (2, 7) 计算其他方式的距离 :

$\begin{aligned} Distance = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} = \sqrt{(2 - (- 1))^{2} + (7 - 5)^{2}} = \sqrt{(3)^{2} + (2)^{2}} = \sqrt{9 + 4} = \sqrt{13} units \end{aligned}$
::距离=(x2-x1)2+(y2-y1)2+(y2-y1)2=(2-(-1))2+(7-5)2=(3)2+(2)2=9+4=13单位

INTERACTIVE

The Distance Formula

Move the red points to change the $x-$ and $y-$ values.
::移动红点以更改 x - 和 y - 值。

Notice how distance is calculated between the points.
::注意如何计算点之间的距离。

Summary

The distance formula states that the distance between $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ is $\begin{aligned} \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} . \end{aligned}$
::距离公式表示(x1,y1)和(x2,y2)之间的距离是(x2-x1)2+(y2-y1)2。

Examples
::实例实例实例实例

Example 1
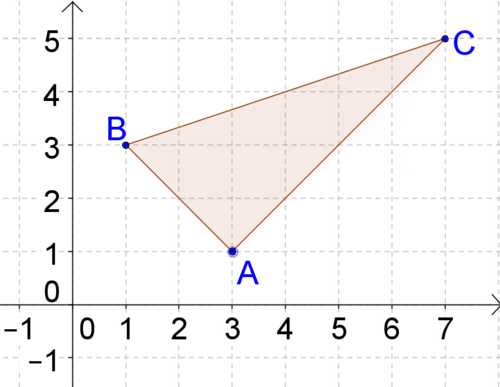
::例1

Find the area of the triangle below.
::查找下方三角形的区域。

Consider the triangle with its three side lengths labeled (lengths found in the above problem ).
::考虑三角形的三边长度标签(长度见上述问题)。

To find the area of the triangle, you can use the formula $\begin{aligned} A = \frac{b h}{2} \end{aligned}$ . Any of the three sides can be the base, but you need a height that is perpendicular to the base you choose. Here, let $\begin{aligned} \bar{A C} \end{aligned}$ be the base, so $\begin{aligned} b = 4.47 units \end{aligned}$
::要找到三角形的区域, 您可以使用公式 A=bh2. 的公式 A=bh2. 。任何三边都可以是基数, 但是您需要与您选择的基数垂直的高度。在这里, 让 AC 成为基数, 所以 b=4. 47 单位

Now, you need to find a line perpendicular to $\begin{aligned} \bar{A C} \end{aligned}$ through point $\begin{aligned} B \end{aligned}$ . $\begin{aligned} \bar{A C} \end{aligned}$ has a slope of $\begin{aligned} \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{3 - 1}{3 - (- 1)} = \frac{2}{4} = \frac{1}{2} \end{aligned}$ . A line perpendicular to $\begin{aligned} \bar{A C} \end{aligned}$ will have a slope of -2. You need to find a line with a slope of -2 that passes through the point $\begin{aligned} (1, 4) \end{aligned}$ .
::现在,您需要通过 B点找到一条与 AC 垂直的线。 AC 的斜坡为 y2 - y1x2 - x1=3 - 13 - (-1) = 24= 12。与 AC 垂直的线的斜坡为 - 2 。您需要找到一条线, 斜坡为 - 2, 穿过点(1, 4 ) 。

$\begin{aligned} y & = m x + b \\ 4 & = - 2 (1) + b \\ 6 & = b \end{aligned}$
::y=mx+b4=2(1)+b6=b

The equation is $\begin{aligned} y = - 2 x + 6 \end{aligned}$ .
::方程式是 y2x+6 。

Next, you need to find where this line intersects $\begin{aligned} \bar{A C} \end{aligned}$ . The equation of the line that contains $\begin{aligned} \bar{A C} \end{aligned}$ is $\begin{aligned} y = \frac{1}{2} x + \frac{3}{2} \end{aligned}$ . Solve the system of equations to find the point of intersection of $\begin{aligned} y = - 2 x + 6 \end{aligned}$ and $\begin{aligned} y = \frac{1}{2} x + \frac{3}{2} \end{aligned}$
::下一步, 您需要找到这条线交叉 AC 。包含 AC 的线的方程式是 y= 12x+32。解决方程式系统以找到 y2x+6 和 y= 12x+32 的交叉点

The point of intersection is $\begin{aligned} (1.8, 2.4) \end{aligned}$ .
::交叉点是(1.8,2.4)。

Next, you need to find the height, which is the distance from $\begin{aligned} (1.8, 2.4) \end{aligned}$ to $\begin{aligned} (1, 4) \end{aligned}$ .
::接下来,您需要找到高度,也就是从1.82.4到1.4的距离。

$\begin{aligned} h = \sqrt{(1.8 - 1)^{2} + (2.4 - 4)^{2}} = 1.79 units \end{aligned}$
::h=(1.8-1-1)2+(2.4-4)2=1.79单位

Now that you know the lengths of the base and the height , you can find the area of the triangle. The area of the triangle is:
::既然您知道基数和高度的长度,您可以找到三角形的区域。三角形的区域是:

$\begin{aligned} A & = \frac{b h}{2} \\ A & = \frac{(4.47) (1.79)}{2} \\ A & \approx 4 {unit}^{2} \end{aligned}$
::A=bh2A=(4.47)(1.792A=4单位2)

Example 2
::例2

Find the perimeter of the rectangle below.
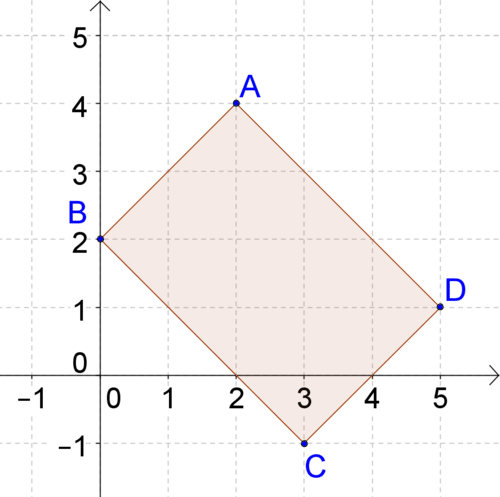
::找出下面矩形的周边

Because the polygon is a rectangle, its opposite sides are the same length . Use the distance formula to find the length of two of the sides.
::由于多边形是一个矩形, 其对面的长度相同。使用距离公式来找到两边的长度。

$\begin{aligned} A B & = \sqrt{(- 2 - 1)^{2} + (4 - 3)^{2}} = \sqrt{(- 3)^{2} + (1)^{2}} = \sqrt{9 + 1} = \sqrt{10} \\ B C & = \sqrt{(1 + 1)^{2} + (3 + 3)^{2}} = \sqrt{(2)^{2} + 6^{2}} = \sqrt{4 + 36} = \sqrt{40} = 2 \sqrt{10} \end{aligned}$
::AB=(-2--1)2+(4-3)2+(3)2+(3)2+(2)2=(3)2+(1)2=9+1=10BC=(1+1)2+(3+3)2=(2)2+62=4+36=40=210

The perimeter of the rectangle is:
::矩形的周边是:

$\begin{aligned} P = \sqrt{10} + 2 \sqrt{10} + \sqrt{10} + 2 \sqrt{10} = 6 \sqrt{10} units \end{aligned}$
::P=10+210+10+10+210=610个单位

Example 3
::例3

Find the area of the rectangle from Example #2.
::从例2中查找矩形区域。

To find the area of the rectangle, use the formula $\begin{aligned} A = b h \end{aligned}$ . The base and the height lengths were found in Example #2.
::要找到矩形区域,请使用公式A=bh。在例2中发现了基数和高度长度。

$\begin{aligned} A & = (\sqrt{10}) (2 \sqrt{10}) \\ A & = 20 {unit}^{2} \end{aligned}$
::A=10(10)(210)A=20单位2

Example 4
::例4

Find the distance between $\begin{aligned} (- 16, 4) \end{aligned}$ and $\begin{aligned} (312, 211) \end{aligned}$ . How does this calculation help to show why having the distance formula is helpful?
::查找( -16 4) 和 (312 211) 之间的距离。此计算如何帮助显示为什么使用距离公式有用 ?

Let $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ $\begin{aligned} = (- 16, 4) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) = (312, 211) \end{aligned}$ .
::Let (x1,y1) = (- 16, 4) 和 (x2, y2) = (312, 211) 。

$\begin{aligned} d = \sqrt{(328)^{2} + (207)^{2}} = \sqrt{107584 + 42849} = \sqrt{150433} \approx 387.86 units \end{aligned}$
::d= (328)2+(207)2=107584+42849=150433387.86 单位

Because these two points are so far apart, it would have been unrealistic to plot them and try to find the distance between them by drawing in a right triangle and using the Pythagorean Theorem. The distance formula makes these types of calculations much quicker.
::因为这两个点相距如此之远,所以绘制它们并试图通过绘制右三角并利用毕达哥伦理论来找到它们之间的距离是不切实际的。距离公式使得这些类型的计算速度更快。

CK-12 PLIX: Taxicab Distance
::CK-12 PLIX: 税区距离

Review
::审查审查审查审查

Find the distance between each pair of points.
::查找每对点之间的距离。

1. $\begin{aligned} (7, 11) \end{aligned}$ and $\begin{aligned} (4, 23) \end{aligned}$ .
::1. (7.11)和(4.23)。

2. $\begin{aligned} (19, 56) \end{aligned}$ and $\begin{aligned} (- 21, 45) \end{aligned}$ .
::2. (19,56)和(21,45)。

3. $\begin{aligned} (- 11, 91) \end{aligned}$ and $\begin{aligned} (89, 16) \end{aligned}$ .
::3. (-11,91)和(89,16)。

For #4-#5, use the rectangle below.
::4 -5,请使用下面的矩形。

4. Find the perimeter of the rectangle.
::4. 找出矩形的周边。

5. Find the area of the rectangle.
::5. 找出矩形区域。

For #6-#7, use the triangle below.
::6 -7,请使用下面的三角形

6. Find the perimeter of the triangle.
::6. 找出三角形的周边。

7. Find the area of the triangle.
::7. 找到三角形的区域。

For #8-#9, use the rectangle below.
::8 -9,请使用下面的矩形。

8. Find the perimeter of the rectangle.
::8. 找出矩形的周边。

9. Find the area of the rectangle.
::9. 寻找矩形区域。

For #10-#11, use the triangle below.
::10 -11,请使用下面的三角形。

10. Find the perimeter of the triangle.
::10. 找出三角形的周边。

11. Find the area of the triangle.
::11. 找到三角形的区域。

For #12-#14, find the perimeter of each polygon.
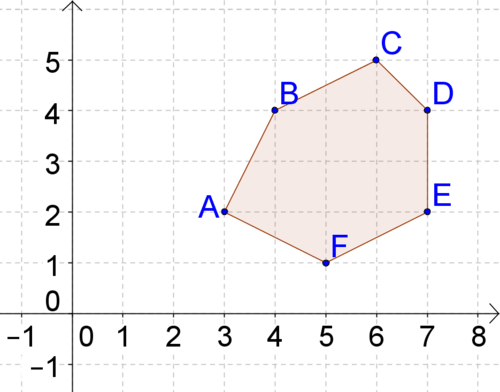
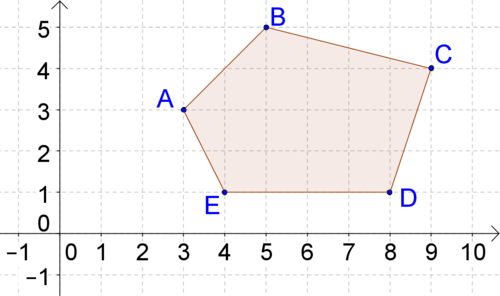
::寻找每个多边形的周界

12.

13 .

14.

15. What does the distance formula have to do with the Pythagorean Theorem?
::15. 距离公式与毕达哥伦神话有什么关系?

16. A triangle has vertices A(-3, -6), B(-1, 5), and C(2, 3). Determine if the triangle is equilateral, scalene, or isosceles.
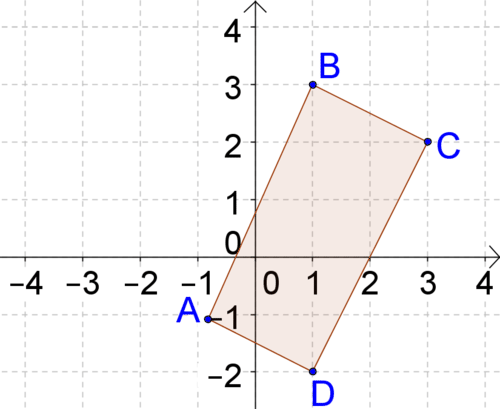
::16. 三角形有A(-3-6)、B(-1、5)和C(2.3),确定三角形是等边形、缩放或等呈。

17. Four points create a shape $\begin{aligned} A B C D . \end{aligned}$ You are given the points A(6, 8), B(14, 6), C(-1, -3), and D(-9,-1). Can you determine what kind of figure this is? Justify your answer.
::17. 四点形成 ABCD 形状。给您给出了 A( 6, 8) 、 B( 14, 6) 、 C( 1, - 3) 和 D( 9, 1) 点。您能确定这是什么样的数字吗? 请说明答案。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

距离公式

Finding Perimeter Using Distance Formula ::使用远程公式查找周边

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX: Taxicab Distance ::CK-12 PLIX: 税区距离

Review ::审查审查审查审查

Review (Answers) ::审查(答复)