课程： 11.1 事件描述-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

事件描述

Experiments, Events, Sample Spaces, and Outcomes
::实验、事件、样本空间和结果

In the context of probability , an experiment is any occurrence that can be observed. For example, rolling a pair of dice and finding the sum of the numbers is an experiment .

An outcome is one possible result of the experiment. So, for the experiment of rolling a pair of dice and finding the sum of the numbers, one outcome is a "7" and a second outcome is an "11".
::实验的结果可能是实验的结果之一。因此,对于滚动一对骰子的实验和找到数字的总和来说,一个结果就是“7”,第二个结果就是“11”。

Every experiment has one or more outcomes . The sample space , $\begin{aligned} S, \end{aligned}$ of an experiment is the set of all possible outcomes. For the experiment of rolling a pair of dice and finding the sum of the 2 numbers on the dice, the sample space is $\begin{aligned} S = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} \end{aligned}$ .
::每个实验都有一个或多个结果。实验的样本空间S是所有可能的结果的一组。对于滚动一对骰子和在骰子上找到2个数字的总和的实验, 样本空间是S2,3,4,5,6,7,7,8,9,9,10,11,12}。

Often there may be one or more outcomes that you are particularly interested in. For example, perhaps you are interested in the sum of the numbers on the dice being greater than five . That event , $\begin{aligned} E, \end{aligned}$ would be a subset of the total sample space that includes only the outcomes you are interested in (sometimes called the favorable outcomes ). If $\begin{aligned} E \end{aligned}$ is the sum of the numbers on the dice being greater than five, then $\begin{aligned} E = {6, 7, 8, 9, 10, 11, 12} . \end{aligned}$ There are many possible events that could be considered for any given experiment.
::通常会出现一种或多种你特别感兴趣的结果。例如, 也许你对骰子上数字的总和超过五倍感兴趣。该事件 E 将是全部样本空间的子集, 它只包含您感兴趣的结果( 有时称为有利结果 ) 。如果骰子上数字的总和超过五倍, 那么 E 6, 7, 8, 9, 9, 10, 11, 12} 。许多可能的事件可以被考虑用于任何特定实验。

There are three common operations to consider with one or more events, shown in the table below. Consider the experiment of rolling a pair of dice and finding the sum of the numbers on the dice. Let event $\begin{aligned} E \end{aligned}$ (see image below table) be "the sum of the 2 numbers is greater than five" $\begin{aligned} (E = {6, 7, 8, 9, 10, 11, 12}) . \end{aligned}$ Let event $\begin{aligned} F \end{aligned}$ be "the sum of the 2 numbers is even" $\begin{aligned} (F = {2, 4, 6, 8, 10, 12}) \end{aligned}$ .
::有三个共同操作要考虑一个或一个以上事件,如下表所示。考虑滚动骰子和在骰子上找到数字总和的实验。 Let event E( 见下表) 是“ 两个数字的总和大于五个”( E6, 8, 9, 9, 10, 11, 12}) 。 Let event F 是“ 两个数字的总和是偶数”( F2, 4, 6, 8, 8, 10, 12} )。

Operation ::业务业务	Definition in Words ::字词的定义	Pair of Dice Example ::相对骰子示例
Complement of an Event $\begin{aligned} (E^{'}) \end{aligned}$ ::活动的补充(E_)	The event that includes all outcomes in the sample space NOT in event $\begin{aligned} E \end{aligned}$ . ::包含样本空间所有结果的事件, 而不是事件 E 。	$\begin{aligned} E^{'} = {1, 2, 3, 4, 5} \end{aligned}$ ::E1,2,3,4,5}欧1,2,3,4,5} $\begin{aligned} E^{'} \end{aligned}$ is "the sum of the numbers on the dice is five or less ." ::是"骰子上数字的总和是五或更少"
Union of Events $\begin{aligned} (E \cup F) \end{aligned}$ ::活动联合会(EF)	The event that includes all outcomes in either event $\begin{aligned} E \end{aligned}$ , event $\begin{aligned} F \end{aligned}$ , or both. ::包含事件E、事件F或同时包含所有结果的事件。	$\begin{aligned} E \cup F = {2, 4, 6, 7, 8, 9, 10, 11, 12} \end{aligned}$
Intersection of Events $\begin{aligned} (E \cap F) \end{aligned}$ ::事件交叉(EF)	The event that includes only the outcomes that occur in both event $\begin{aligned} E \end{aligned}$ and event $\begin{aligned} F \end{aligned}$ . ::只包括事件E和事件F结果的事件。	$\begin{aligned} E \cap F = {6, 8, 10, 12} \end{aligned}$

To help visualize the way different events or combinations of events interact within a sample space, consider a .
::为帮助想象不同事件或事件组合在样本空间内相互作用的方式,请考虑。

The diagram above has a big rectangle for sample space $\begin{aligned} S \end{aligned}$ . Within $\begin{aligned} S, \end{aligned}$ all possible outcomes 2 through 12 appear in various places. The circle labeled $\begin{aligned} E \end{aligned}$ represents event $\begin{aligned} E \end{aligned}$ " the sum of the numbers is greater than five ," and within that circle are all the outcomes in event $\begin{aligned} E \end{aligned}$ . Similarly, the circle labeled $\begin{aligned} F \end{aligned}$ represents event $\begin{aligned} F \end{aligned}$ " the sum of the numbers is even ," and within that circle are all the outcomes in event $\begin{aligned} F . \end{aligned}$ The place where the circles overlap contains only the outcomes that are in both events $\begin{aligned} E \end{aligned}$ and $\begin{aligned} F . \end{aligned}$
::上面的图表对样本空间 S. 在 S 中, 所有可能的结果 2 至 12 都出现在多个地方。标为 E 的圆环代表 E 事件 E “ 数字之和大于 5 ” , 而在这个圆圈中, 则代表 E 事件的所有结果。同样, 标为 F 的圆形代表 F “ 数字之和是均匀的 ” , 在那个圆圈中, 也代表 F 事件的所有结果。圆圈重叠的地方只包含 E 和 F 事件的结果。

Describing Events
::描述事件

Consider the area of the diagram above that represents "Not $\begin{aligned} F \end{aligned}$ " ( $\begin{aligned} F^{'} \end{aligned}$ ). Describe the event $\begin{aligned} F^{'} . \end{aligned}$
::考虑上面图中代表“非F”(F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_F_BAR_F_F_BAR_F_F_F_F_F_F_BAR_F_F_F_F_F_F_F_BAR_F_F_F_F_BAR_F_F_F_F_F_BAR_F_F_F_F_BAR_F_F_F_F_BAR_BAR_BAR_BAR_F_F_F_F_F_F_F_F_F_BAR_F_F_BAR_F_F_F_F_F_BAR_F_F_F_F_F_F_F_F_F_F_BAR_BAR_F_F_F_F_F_F_F_BBBBBBBF_F_F_F_F_F_F_

$\begin{aligned} F^{'} \end{aligned}$ is the complement of event $\begin{aligned} F . \end{aligned}$ It contains all the outcomes in the sample space that are NOT in event $\begin{aligned} F \end{aligned}$ .
::F`是事件F的补充。F.它包含样本空间中所有非事件F的结果。

In this case, $\begin{aligned} F^{'} \end{aligned}$ is the sum of the numbers on the dice being odd, since it is all the numbers whose sum is not even.
::在这种情况下,F`是骰子上数字的奇数之和,因为所有数字的数值都不相等。

Union vs. Intersection
::工会对跨部门

Consider the area of the diagram below that represents $\begin{aligned} E \cup F \end{aligned}$ . Then, consider the area of the diagram that represents $\begin{aligned} E \cap F \end{aligned}$ . How is the union of two events different from the intersection of two events?
::考虑下图中代表 EQF 的面积。然后考虑图中代表 EQF 的面积。两个事件的结合与两个事件的交点有何不同?

$\begin{aligned} E \cup F \end{aligned}$ is the union of events $\begin{aligned} E \end{aligned}$ and $\begin{aligned} F \end{aligned}$ . It contains all the outcomes that are in event $\begin{aligned} E \end{aligned}$ , event $\begin{aligned} F \end{aligned}$ , or both events E and $\begin{aligned} F \end{aligned}$ . The symbol $\begin{aligned} \cup \end{aligned}$ can be thought of as "or", but remember that it is not exclusive or, since it includes outcomes that are in both events. $\begin{aligned} E \cup F \end{aligned}$ is shown below.
::EF是活动的E和F的结合。它包含事件E、事件F或事件E和F的所有结果。这个符号可以被认为是“或”,但记住它不是排他性的,或者因为它包括两个活动的结果。 EF如下表所示。

$\begin{aligned} E \cap F \end{aligned}$ is the intersection of events $\begin{aligned} E \end{aligned}$ and $\begin{aligned} F \end{aligned}$ . It contains all the outcomes that are in both events $\begin{aligned} E \end{aligned}$ and $\begin{aligned} F \end{aligned}$ . The symbol $\begin{aligned} \cap \end{aligned}$ can be thought of as "and", since it includes only the outcomes that are in both events. $\begin{aligned} E \cap F \end{aligned}$ is shown below.
::EF是事件E和F的交叉点。它包含两个事件EandF中的所有结果。符号“ 和”, 因为它只包括两个事件的结果。 EF 如下所示。

Notice that $\begin{aligned} E \cup F \end{aligned}$ will always contain the same outcomes as $\begin{aligned} E \cap F \end{aligned}$ , plus more outcomes (usually). $\begin{aligned} E \cup F \end{aligned}$ could never contain less outcomes than $\begin{aligned} E \cap F \end{aligned}$ .
::请注意,EF总是包含与EF相同的结果,加上更多的结果(通常情况下 ) 。 EF永远不会包含比EF更少的结果。

INTERACTIVE

Dice Roll

Click the "Generate Roll" button to roll two dice and see where their total sum lands on or outside the Venn Diagram.
::单击“ Generate Roll” 按钮滚动两骰子,看看他们的总和在 Venn 图表上方或外方的位置。

The sum will be highlighted in red within the Venn diagram.
::在Venn图中将以红色标出总和。

Use the drop-down menu to view all the possible events for sets E and F.
::使用下拉菜单查看 E 和 F 组的所有可能事件。

Experimental Outcomes
::实验结果

Consider the experiment of tossing three coins and recording the sequence of heads and tails. Let $\begin{aligned} A \end{aligned}$ be the event "there are exactly two heads." Let $\begin{aligned} B \end{aligned}$ be the event "there are exactly two tails."
::试想一下扔三个硬币和记录头和尾的顺序。让事件“正好有两个头 ” 。事件“正好有两个尾巴 ” 。事件“正好有两个尾巴 ” 。

Typically when working with experiments having to do with coins, $\begin{aligned} H \end{aligned}$ commonly represents getting "heads" and $\begin{aligned} T \end{aligned}$ getting "tails."
::通常在做与硬币有关的实验时,H通常表示得到“头”和T得到“尾”。

a) Find the sample space for the experiment.
:a) 寻找实验的样本空间。

The same sample is: $\begin{aligned} S = {H H H, H H T, H T H, T H H, H T T, T H T, T T H, T T T} \end{aligned}$
::同样的样本是:SHHH,HHT,HHT,HHH,HHT,THT,TTT}

b) List the outcomes in event $\begin{aligned} A \end{aligned}$ .
:b) 列出事件A的结果。

$\begin{aligned} A = {H H T, H T H, T H H} \end{aligned}$
::呵呵,呵呵,呵呵

c) List the outcomes in event $\begin{aligned} B \end{aligned}$ .
:c) 列出事件B的结果。

$\begin{aligned} B = {H T T, T H T, T T H} \end{aligned}$
::BHT,THT,THT,THT}(BHTT,THTT,THT) (BHTT,THTT,THTT,THT)

d) Create a diagram that shows the sample space, events $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ , and all of the outcomes.
:d) 绘制一个图表,显示样本空间、事件A和B以及所有结果。

Notice that this time there are no outcomes that are in both $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ , so the circles don't overlap.
::注意这次A和B都没有结果所以圈圈不会重叠

Examples
::实例实例实例实例

Example 1
::例1

You pick a card from a standard deck. Event $\begin{aligned} C \end{aligned}$ is choosing a card that has an even number or a spade. Rewrite event $\begin{aligned} C \end{aligned}$ as the of two events. Then, list the outcomes in event $\begin{aligned} C \end{aligned}$ .
::您可以从标准甲板中选择一张牌。事件C 选择一张有偶数或对调的牌。重写事件C 作为两个事件。然后, 列出事件C 的结果。

There are 52 cards in a standard deck of cards. These 52 cards are organized by suit:
::标准牌牌牌牌有52张牌,这52张牌是西装牌:

Spades : Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King
::Spades: A, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, Jack, Queen, King. A, 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, K.

Diamonds : Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King
::钻石: A, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King 钻石: A, 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, K.

Clubs : Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King
::Clubs: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King. Ace, 2, 3, 3, 4, 4, 5, 6, 6, 7, 8, 9, 10, Jack, Queen, King.

Hearts : Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King
::爱心: A, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King

Event $\begin{aligned} C \end{aligned}$ is choosing a card that has an even number or a spade on it. Because the word "or" is used, you know this is really the union of two other events. Let event $\begin{aligned} D \end{aligned}$ be choosing an even number and let event $\begin{aligned} E \end{aligned}$ be choosing a spade. Then $\begin{aligned} C = D \cup E \end{aligned}$ .
::事件 C 是选择一个有偶数的卡片, 或有平方块。因为使用了“ 或” 一词, 您知道这实际上是另外两个事件的组合。让事件 D 选择一个偶数, 让事件 E 选择一个平方块。然后是 C=DE 。

$\begin{aligned} D = \end{aligned}$ {2 of clubs, 4 of clubs, 6 of clubs, 8 of clubs, 10 of clubs, 2 of diamonds, 4 of diamonds, 6 of diamonds, 8 of diamonds, 10 of diamonds, 2 of hearts, 4 of hearts, 6 of hearts, 8 of hearts, 10 of hearts, 2 of spades, 4 of spades, 6 of spades, 8 of spades, 10 of spades}
::D= {俱乐部2, 俱乐部4, 俱乐部6, 俱乐部8, 俱乐部10, 钻石2, 钻石4, 钻石6, 钻石8, 钻石10, 红心2, 红心4, 红心6, 红心8, 红心10, 黑桃2, 黑桃4, 黑桃6, 黑桃8, 黑桃10}

$\begin{aligned} E = \end{aligned}$ {Ace of spades, 2 of spades, 3 of spades, 4 of spades, 5 of spades, 6 of spades, 7 of spades, 8 of spades, 9 of spades, 10 of spades, Jack of spades, Queen of spades, King of spades}
::{黑桃A, 黑桃 2, 黑桃 3, 黑桃 4, 黑桃 5, 黑桃 6, 黑桃 7, 黑桃 8, 黑桃 9, 黑桃 10, 黑桃 Jack, 黑桃女王, 黑桃之王}

$\begin{aligned} C = D \cup E = \end{aligned}$ {Ace of spades, 2 of spades, 3 of spades, 4 of spades, 5 of spades, 6 of spades, 7 of spades, 8 of spades, 9 of spades, 10 of spades, Jack of spades, Queen of spades, King of spades, 2 of clubs, 4 of clubs, 6 of clubs, 8 of clubs, 10 of clubs, 2 of diamonds, 4 of diamonds, 6 of diamonds, 8 of diamonds, 10 of diamonds, 2 of hearts, 4 of hearts, 6 of hearts, 8 of hearts, 10 of hearts}
::{黑桃、2黑桃、3黑桃、4黑桃、5黑桃、6黑桃、7黑桃、8黑桃、9黑桃、10黑桃、黑桃杰克、黑桃女王、黑桃国王、2梅花、4梅花、6梅花、8梅花、8梅花、10梅花、2钻石、4钻石、6钻石、8钻石、10钻石、2红桃、4红桃、6红桃、8红桃、10红桃}

Consider the experiment of tossing three coins and recording the sequence of heads and tails. The diagram below represents the sample space and two events $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ .
::下图显示了样本空间和两个事件A和B。

Example 2
::例2

Describe $\begin{aligned} A^{'} \end{aligned}$ in words and with a diagram. What outcomes are in this event?
::用文字和图表来描述A_A_A_A_A_A_A_BAR__BAR_A_A_A_A_A_BAR__BAR_A_A_A_A_A_BAR_A_A_A_A_A_A_A_A_A_A_BAR_A_A_A_A_A_A_BAR_A_A_A_A_A_A_BAR_A_A_A_A_A_A_BAR__BAR_A_BAR_A_A_A_A_A_BAR_A_A_A_A_A_BAR_A_A_A_A_A_BAR_A_A_A_A_A_BAR_A_A_A_A_A_A_A_BAR_A_A_A_A_A_BAR_BAR_A_A_A_A_BAR_A_A_A_A_A_BAR_A_A_A_A_A_A_A_A_A_A_BAR_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_BAR_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_A_

$\begin{aligned} A \end{aligned}$ is the event " getting exactly two heads ."
$\begin{aligned} A^{'} \end{aligned}$ is the event " not getting exactly two heads ."
::A是“一对一”事件 A是“一对一”事件 A是“一对二”事件 A是“一对二”事件 A是“一对二”事件 A是“一对二”事件

$\begin{aligned} A^{'} = {T T H, T H T, H T T, H H H, T T T} . \end{aligned}$ On the diagram, it is everything in the rectangle except circle $\begin{aligned} A \end{aligned}$ .
::在图表上,除了A圆外,所有东西都在矩形中。

Example 3
::例3

Describe $\begin{aligned} (A \cup B) \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::用文字和图表来描述(AB)。在这种情况下,结果如何?

$\begin{aligned} (A \cup B) \end{aligned}$ is all of the outcomes in event $\begin{aligned} A \end{aligned}$ , event $\begin{aligned} B \end{aligned}$ , or both . Note that for this experiment, there are no events in both $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ . $\begin{aligned} A \cup B \end{aligned}$ $\begin{aligned} = {H H T, H T H, T H H, T T H, T H T, H T T} \end{aligned}$ . In the diagram, only circles $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ are shaded.
:AB) 是事件A, 事件B, 或者两者中的全部结果。请注意, 对于此项实验, ABHHT, HHT, HHH, TTH, TH, THT, HTT} 都不存在任何事件。在图表中, 只有圆 A和 B 有阴影。

Example 4
::例4

Describe $\begin{aligned} (A \cup B)^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::用文字和图表来描述(AB)______。在这种情况下,结果如何?

$\begin{aligned} (A \cup B)^{'} \end{aligned}$ is all of the outcomes not in $\begin{aligned} (A \cup B) \end{aligned}$ . This means it is all of the outcomes that are in neither events $\begin{aligned} A \end{aligned}$ nor $\begin{aligned} B \end{aligned}$ . $\begin{aligned} (A \cup B)^{'} = {H H H, T T T} \end{aligned}$ . In the diagram, the opposite part of the rectangle is shaded compared with example 3.
:AB)不是全部结果(AB) 。这意味着所有结果既不是事件A也不是事件B。 (AB)HHH,TTT}。在图表中,矩形的反面与例3相比被遮蔽。

Example 5
::例5

Describe $\begin{aligned} (A \cap B)^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::用文字和图表来描述(AB)______。在这种情况下,结果如何?

$\begin{aligned} (A \cap B)^{'} \end{aligned}$ is all of the outcomes not in $\begin{aligned} (A \cap B) \end{aligned}$ . Remember that $\begin{aligned} A \cap B \end{aligned}$ is all of the outcomes in both events $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ ; however, in this experiment the two events don't overlap (they are disjoint).
:AB) 并非全部结果(AB) 。记住, AB 是 A 和 B 事件的所有结果; 但是, 在本次实验中, 这两个事件并不重叠( 它们脱节 ) 。

$\begin{aligned} A \cap B \end{aligned}$ $\begin{aligned} = {} \end{aligned}$ , the empty set. This means that $\begin{aligned} (A \cap B)^{'} \end{aligned}$ must be the whole sample space, since it has to include all outcomes in the sample space not in $\begin{aligned} A \cap B \end{aligned}$ .
::===============================================================B========================================================================================================================================================================================================================================================================================

$\begin{aligned} (A \cap B)^{'} \end{aligned}$ $\begin{aligned} = {H H H, H H T, H T H, T H H, T T H, T H T, H T T, T T T} \end{aligned}$ . In the diagram, everything in the rectangle is shaded.
::在图表中,矩形上的一切都被遮蔽了

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

Probability is the chance that something will happen. It can be written as a fraction, decimal or percent.
::概率是发生某事的几率。它可以写成一个小数、小数或百分比。

An experiment is a process of taking a measurement or making an observation.
::实验是一种测量或观察的过程。

An outcome of a probability experiment is one possible end result.
::概率实验的结果是可能的终极结果。

In a probability experiment, the sample space is the set of all the possible outcomes of the experiment.
::在概率实验中,样本空间是实验所有可能结果的一组。

The word or in mathematics means the union of the sets. Combining both sets into one large set.
::词词或数学中的意思是组合组合的组合。将两个组合合并成一个大组合。

The word and in mathematics means the intersection between the sets. What the sets have in common.
::字词和数学中的词意指各组之间的交叉点。各组之间有哪些共同点。

The compliment (A’) is the event that includes all outcomes in the sample space NOT in event (A).
::赞美(A)是包含样本空间的所有结果的事件,

Review
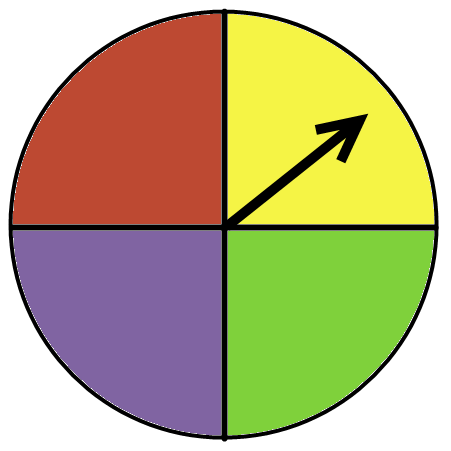
::审查审查审查审查

Consider the experiment of spinning the spinner below twice and recording the sequence of results. Let $\begin{aligned} F \end{aligned}$ be the event that the same color comes up twice. Let $\begin{aligned} H \end{aligned}$ be the event that there is at least one red.
::将旋转器旋转到两次以下并记录结果序列的实验。让 F 成为相同颜色出现两次的事件。让 H 成为至少有一个红色的事件。

1. Find the sample space for the experiment.
::1. 寻找实验的样本空间。

2. List the outcomes in event $\begin{aligned} F \end{aligned}$ and the outcomes in event $\begin{aligned} H \end{aligned}$ .
::2. 列出事件F的结果和事件H的结果。

3. Create a Venn diagram that shows the relationships between the outcomes in $\begin{aligned} F \end{aligned}$ , $\begin{aligned} H \end{aligned}$ , and the sample space.
::3. 绘制文恩图,显示F、H和样本空间结果之间的关系。

4. Describe $\begin{aligned} F^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::4. 用文字和图表来描述F`,在这种情况下有什么结果?

5. Describe the event "getting two reds" with symbols and with the diagram. What outcomes are in this event?
::5. 用符号和图表来描述“产生两个红色”的事件。

6. Describe $\begin{aligned} (F \cup H)^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::6. 用文字和图表说明(FH)____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Consider the experiment of rolling a pair of dice and finding the sum of the numbers on the dice. Let $\begin{aligned} J \end{aligned}$ be the event that the sum is less than 4. Let $\begin{aligned} K \end{aligned}$ be the event that the sum is an odd number.
::想象一下滚动一对骰子的实验, 并在骰子上找到数字的总和。让 J 来决定总和小于 4 。让 K来决定总和是一个奇数。

7. Find the sample space for the experiment.
::7. 寻找实验的样本空间。

8. List the outcomes in event $\begin{aligned} J \end{aligned}$ and the outcomes in event $\begin{aligned} K \end{aligned}$ .
::8. 列出事件J的结果和事件K的结果。

9. Create a Venn diagram that shows the relationships between the outcomes in $\begin{aligned} J, K \end{aligned}$ , and the sample space.
::9. 绘制文恩图,显示J、K和样本空间的结果之间的关系。

10. Describe $\begin{aligned} K^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::10. 用文字和图表来描述K`,在这件事上有什么结果?

11. Describe the event "getting an even number less than 4" with symbols and with the diagram. What outcomes are in this event?
::11. 用符号和图解描述“数字甚至低于4”的事件,在这种情况下结果如何?

12. Describe $\begin{aligned} (J \cap K^{'})^{'} \end{aligned}$ in words and with the diagram. What outcomes are in this event?
::12. 用文字和图表来说明(JK) 。

13. In this experiment, are you just as likely to get a sum of 2 as a sum of 7? Explain.
::13. 在这一实验中,你是否同样可能得到2和7之和?

14. Compare and contrast unions of events with intersections of events.
::14. 比较和对比事件与事件交错的结合。

15. Consider some experiment with event $\begin{aligned} E \end{aligned}$ . Describe $\begin{aligned} E \cup E^{'} \end{aligned}$ . Describe $\begin{aligned} E \cap E^{'} \end{aligned}$ .
::15. 考虑对事件E. 描述E ' E. 描述E ' E. 描述E ' E ' . 描述E ' E ' . 描述E ' E ' .

16. If A is the set of all factors of 36 and B is the set of all factors of 24, explain situations where you might want to find A∪B, A∩B, A', B' , or (A∩B)'.
::16. 如果A是36和B的所有因数的一组,那么,如果A是所有因数的一组,36和B是24的所有因数的一组,请解释您可能想要找到AB、AB、A'、B'或(AB)的情况。

17. Draw a Venn diagram with three overlapping circles. Use your Venn diagram to show that (A∩B)∪C = (A∩C)∩(B∪C). Create a scenario where you would use this information.
::17. 绘制三个重叠圆的文恩图。使用您的文恩图显示 (AB) C = (AC) (BC) 。创建您使用此信息的假想。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

事件描述

Experiments, Events, Sample Spaces, and Outcomes ::实验、事件、样本空间和结果

Describing Events ::描述事件

Union vs. Intersection ::工会对跨部门

Experimental Outcomes ::实验结果

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

CK-12 PLIX Interactive ::CK-12 PLIX 交互式互动

Review ::审查审查审查审查

Review (Answers) ::审查(答复)