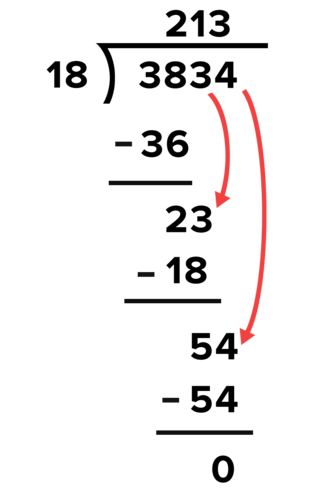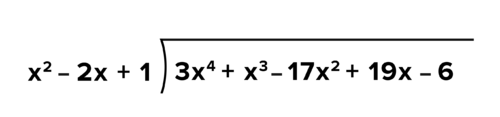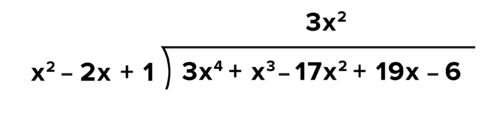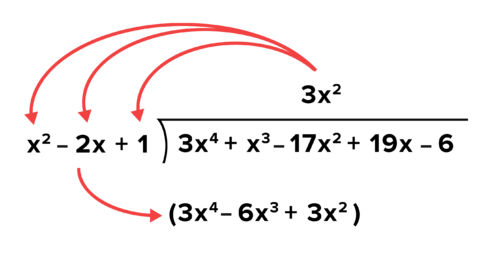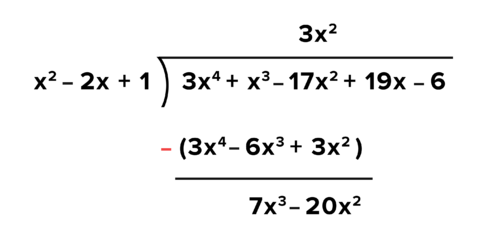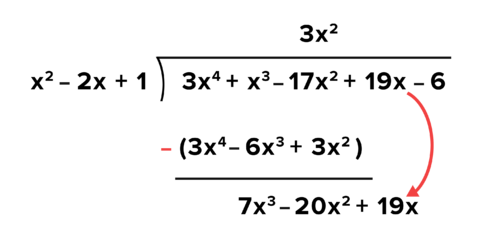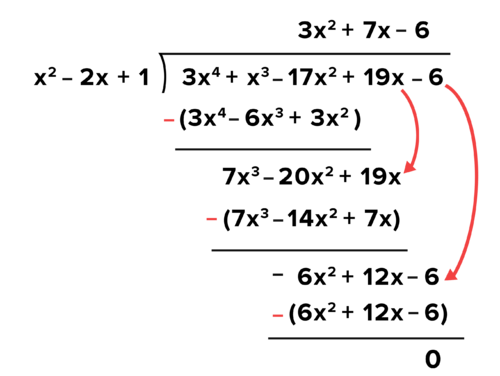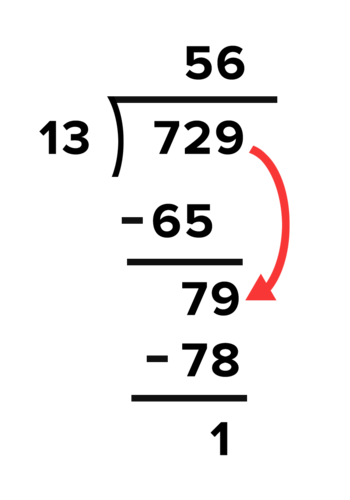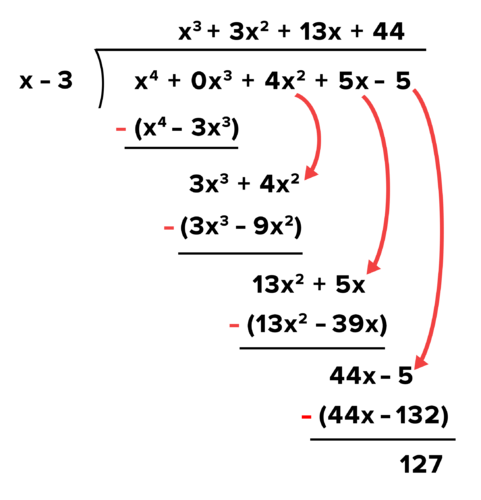1.4 分裂的多面体-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节分裂的多面体

  折叠 展开

  分裂的多面体

  播放段落

  Learning Objectives
  ::学习目标

  播放段落
  • Divide using the box method.
    ::使用框法除法。
  播放段落
  • Divide polynomials using long division .
    ::使用长除法除以多面性 。
  播放段落
  • Understand how to find a remainder when .
    ::了解如何找到剩余 当.
  播放段落
  • Divide polynomials within a real-world context.  
    ::在现实世界中将多元性分开。

  ---

  播放段落

  Introduction: Checking Data
  ::导言:核对数据

  

  播放段落

  Polynomial division
  ::多元分裂

  播放段落

  Polynomial division comes up in many situations involving rates and geometric applications. Given all the applications of polynomial multiplication , and knowing that division is the inverse operation of multiplication, this statement should come as no surprise. 
  ::在许多涉及比率和几何应用的情形下,出现了多元分解。 考虑到多元乘法的所有应用,并且知道分解是乘法的逆向作用,本声明不应令人惊讶。

  播放段落

  The lesson " Properties of Polynomials"  discussed how  information is sent in binary notation, which can be modeled using polynomials. When information is received, polynomial division is used to verify that the information was sent properly  using a process called cyclic redundancy check (CRC) . Messages  are sent  with a CRC code  that  is used to check whether the message was altered. If the message (written in binary ) can be divided by the code with no remainder, it is highly likely that no errors occurred during the transmission process. This example is a basic explanation of just one of the many checks that are performed to check for errors.
  ::课程“ 多面体属性” 讨论了信息如何在二进制符号中发送, 该二进制符号可以用多面体模拟。 当收到信息时, 使用多面体分隔来验证信息是否使用称为循环冗余检查( CRC) 的程序正确发送 。 信件的发送使用 CRC 代码来检查信件是否被更改 。 如果信件( 以二进制) 可以用代码分隔, 没有剩余内容, 则在传输过程中很可能没有出错 。 这个示例只是用于检查错误的众多检查之一的基本解释 。

  播放段落

  Use the interactive below to  review how to convert from binary to polynomial notation.  This will be used later in the lesson  to check messages for errors.
  ::使用下面的交互效果来审查如何将二进制符号转换为多义符号。 这将在稍后的课中用于检查信件错误 。

   

  ---

  播放段落

  Activity 1: Understanding Division
  ::活动1:了解司

  播放段落

  Before checking messages for errors, take a look at how  polynomial division works using the box method . 
  ::在检查信件错误前,请先查看多式分区如何使用框方法工作。

  播放段落

  The lesson "Multiplying Polynomials"  discussed  how to multiply polynomials using the box method. Use the interactive below to review polynomial multiplication.
  ::“ 模拟多面性” 课讨论了如何使用框法乘以多面性。 使用下面的交互方法来审查多面性乘法 。

  播放段落

  Since division is the inverse of multiplication, polynomial division can be done by  undoing  the above process.
  ::由于除法是乘法的逆反,多元分法可以通过取消上述程序来完成。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Divide  $\begin{align*}3x^3+x^2−4x\end{align*}$   by  $\begin{align*}x−1.\end{align*}$
  ::除以 3x3+x2 - 4x x x- 1 。

  播放段落

  In arithmetic, t he expression  $\begin{align*}8 \div 2 = 4\end{align*}$   can be written as  $\begin{align*}2 \cdot 4 = 8,\end{align*}$  and since the polynomials above represent numbers,  you can apply this to the example above.
  ::在算术中,表达式 82=4 可以写为 24=8, 由于以上多数值代表数字, 您可以对上例应用此选项 。

  播放段落

  If  $\begin{align*}3x^3+x^2−4x \div x−1 = Q\end{align*}$   where  $\begin{align*}Q\end{align*}$  is the quotient,  the equation can be rewritten as  $\begin{align*}x-1 \cdot Q = 3x^3+x^2−4x.\end{align*}$   U se this to recreate the box which produced the product $\begin{align*}3x^3+x^2−4x.\end{align*}$
  ::如果 Q 是 商数 3x3+x2 - 4xx- 1 , 方程式可以重写为 x- 1 = 3x3+x3+x2 - 4x 。 使用此选项来重建产生 3x3+x2 - 4x 的产物框 。

  播放段落

  In the interactive below,  $\begin{align*}x-1\end{align*}$  will run vertically to represent the rows, and  $\begin{align*}Q\end{align*}$  will run horizontally along the top to represent the columns. Use the interactive to fill out the box .
  ::在下文互动栏中, x-1 将垂直运行以代表行, Q 将沿着顶部水平运行以代表列。 使用交互运行以填充框 。

  播放段落

  Use the box method to solve the following:  $\begin{align*}(3x^3+5x^2+4x−2) \div (3x−1)\end{align*}$
  ::使用框方法解决以下问题( 3x3+5x2+4x-2) ( 3x- 1)

   

   

  ---

  播放段落

  Activity 2: Long Division of Polynomials
  ::活动2:多边协议的长片

  播放段落

  While the method above works, it can get  complicated as the number of terms increases. U se  your knowledge of long division when dividing integers to u nderstand polynomial division . You can use the same algorithm: 
  ::虽然上述方法有效, 但随着语句数的增加, 它会变得复杂。 使用您对长分割法的知识来区分整数来理解多元分割法。 您可以使用相同的算法 :

  播放段落
  1. Divide
     ::除除
  播放段落
  2. Multiply
     ::乘乘乘乘
  播放段落
  3. Subtract
     ::减减
  播放段落
  4. Bring Down
     ::下调 下调
  播放段落
  5. Repeat
     ::重复重复

  

  播放段落

  T ake a look at how this would work with polynomials:
  ::看看这如何与多面体合作:

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Divide  $\begin{align*}(3x^4 + x^3 - 17x^2 + 19x - 6) \div (x^2 -2x + 1)\end{align*}$
  ::除法( 3x4+x3 - 17x2+19x-6) ( x2 - 2x+1)

  播放段落

  Start by writing the division problem  in the same format used  to write long division with numbers. The dividend,  $\begin{align*}(3x^4 + x^3 - 17x^2 + 19x - 6),\end{align*}$  always goes inside, and the divisor,  $\begin{align*}(x^2 -2x + 1),\end{align*}$  always goes outside.
  ::开始以写有数字的长除法时所用的相同格式写出分裂问题。 红利( 3x4+x3- 17x2+19x-6) 总是会进入内部, divisor ( x2-2x+1) 总是会进入外部 。

  播放段落

  Every term of the polynomial should be written, including any missing terms, to prevent issues when lining up terms by degree . For example, the polynomial  $\begin{align*}x^2 + 3\end{align*}$  has an  $\begin{align*}x^1\end{align*}$  term missing. This term is missing because the coefficient of the  $\begin{align*}x^1\end{align*}$  term is 0. To address this, write  $\begin{align*}x^2 + 3\end{align*}$  as  $\begin{align*}x^2 + 0x + 3.\end{align*}$
  ::多义的每个术语都应写入, 包括任何缺失的术语, 以防止在按度排列术语时出现问题。 例如, 多义 x2+3 缺少一个 x1 术语。 由于 x1 术语的系数为 0, 此术语缺失 。 要解决这个问题, 请将 x2+3 写入 x2+0x+3 。

  

  播放段落

  1. Divide
  ::1. 除数

  播放段落

  To begin, figure out  how many times the leading term in the divisor goes into the leading term in the dividend . Another way to phrase this is “ $\begin{align*}x^2\end{align*}$  times what is $\begin{align*}3x^4\end{align*}$ ?”
  ::首先,要找出“三维”中前一术语进入股息前一术语的几倍。 另一种用词是“x2乘以3x4? ” (x2乘以3x4 ) 。

  

  播放段落

  2. Multiply
  ::2. 乘乘数

  播放段落

  Since  $\begin{align*}x^2\end{align*}$  goes into  $\begin{align*}3x^4,\: 3x^2\end{align*}$  times,  you need to multiply  $\begin{align*}3x^2\end{align*}$  by the entire divisor and write the product  underneath the quotient.
  ::由于 x2 进入 3x4, 3x2 倍, 您需要将 3x2 乘以整个 divisor , 并将产品写在商数下 。

  

  播放段落

  3. Subtract
  ::3. 减减

  播放段落

  The next step is to subtract the product from S tep 2 by the like terms in the dividend. At each new 'level' of long division,  subtract  the entire polynomial. Be  careful   when subtracting a negative term, which is equivalent to adding a positive term.
  ::下一步是将第2步的产品从“ 步骤2” 中减去同样的红利条件。 在“ 步骤2” 中, 将“ 步骤2” 中的产品从“ 步骤2” 中减去。 在“ 步骤2” 中, 将“ 步骤2” 中的产品从“ 步骤2” 中减去相同的条件。 在“ 步骤2” 中, 将“ 步骤2” 中的产品从“ 步骤2” 中减去, 将“ 步骤2” 中的产品从“ 步骤2” 中减去相同的条件。 在“ 步骤2” 中, 在“ 步骤2” 中, 将“ 步骤2” 中的产品从“ 步骤2” 中减去, 在“ 步骤2” 中, 在“ 步骤2” 中, 将“ 步骤2” 中, 在“ 步骤2” 的“ 步骤” 中, 以“ 步骤” 等值减去“ 。 在“ 步骤” 中, 步骤中, 下一步是将“ 。 在“ 步骤2” 中, “ 步骤2” 中, 步骤中, 将“ 步骤中“ 步骤2” 的“ 步骤” 步骤” 将“ 将“ 的“ 中, 将“ 步骤2” 的“ 减为“ 中” 中” 。“ 中” 。“ 。“ 中, 。“ 中” 。“ 中” 中, , 步骤” 将“ 中,将“ 步骤” 改为“ 改为“ 改为“ 中” 步骤” 。“ 。“ 。“ 。” 。 “ 步骤” 。“ ” 。“ ” ” 。“ ” ” ” ” ” 。“步骤” , ” 。“步骤” 将“步骤” 。“步骤” 将“步骤” 。“步骤” 。“步骤” 。“步骤” ” 。“步骤” 。“步骤” 以“步骤” 以“步骤” 将“步骤” ,“步骤”改为“步骤”改为“步骤” ,将“

  

  播放段落

  4. Bring Down
  ::4. 下调

  播放段落

  As with long division of integers, after subtracting, bring down the next term in the dividend.
  ::与长的整数分割一样,减去后,将红利的下一期减为下期。

  

  播放段落

  5. Repeat
  ::5. 重复

  播放段落

  Repeat the steps above, dividing the divisor into the polynomial resulting from S tep 4. You can think of this polynomial as the new dividend. This polynomial represents what remains after dividing  $\begin{align*}3x^2\end{align*}$  out of the original dividend. The next step is to divide  $\begin{align*}x^2\end{align*}$   into  $\begin{align*}7x^3.\end{align*}$  The remaining steps can be seen below.
  ::重复以上步骤, 将二进制分为四进制产生的多元值, 您可以将这一多元值视为新红利。 此多元值代表将3x2从原始红利中分离出来之后的剩余值。 下一步是将 x2 分为 7x3 。 剩下的步骤可以在下面看到 。

  

  播放段落

  Answer:   $\begin{align*}(3x^4 + x^3 - 17x^2 + 19x - 6) \div (x^2 -2x + 1) = 3x^2 + 7x - 6\end{align*}$
  ::答复: (3x4+x3- 17x2+19x-6) (x2-2x+1) = 3x2+7x-6

  播放段落

  Since there is no remainder,  $\begin{align*}x^2 -2x + 1\end{align*}$  goes into  $\begin{align*}3x^4 + x^3 - 17x^2 + 19x - 6\end{align*}$   evenly ,  $\begin{align*}3x^2 + 7x - 6\end{align*}$  times.
  ::由于没有剩余部分, x2-2x+1以3x4+x3 - 17x2+19x-6平均,3x2+7x-6乘以3x4+3 - 17x2+19x-6。

  播放段落

  In the same way that  $\begin{align*}18 \cdot 213 = 3,834,\end{align*}$   you can state that  $\begin{align*}(x^2 -2x + 1)(3x^2 + 7x - 6) = 3x^4 + x^3 - 17x^2 + 19x - 6.\end{align*}$
  ::同样,18213=3,834, 您可以声明 (x2-2x+1)(3x2+7x-6) = 3x4+x3-17x2+19x-6) = 3x4+17x2+19x-6。

  播放段落

  M ultiply those factors to check  your answer. Since there is no remainder, both  $\begin{align*}x^2 -2x + 1\end{align*}$  and  $\begin{align*}3x^2 + 7x - 6\end{align*}$  are factors of  $\begin{align*}3x^4 + x^3 - 17x^2 + 19x - 6.\end{align*}$
  ::乘以这些系数来检查您的答复。由于没有剩余值, x2-2x+1 和 3x2+7x-6 均为 3x4+x3-17x2+19x-6 的系数。

   

  ---

  播放段落

  Activity 3: Remainders
  ::活动3:保留者

  播放段落

  The introduction discussed how  programs use polynomial division to determine whether or not transmitted information like text messages, emails, etc. were corrupted in the sending process. Once a message is received, the polynomial is divided by a generator polynomial sent with the message. If there is a remainder, the message was corrupted.
  ::介绍中讨论了程序如何使用多元分解来确定发送过程中是否损坏了像短信、电子邮件等信息。 收到信件后, 多元分解由生成器多元分解与信件一起发送。 如果还有剩余信息, 则该信件被损坏 。

  播放段落

  W hat would a remainder look like in polynomial division?
  ::在多民族分裂中,剩下的人会是什么样子?

  播放段落

  Recall that with integers, the  remainder  could be written as a fraction .
  ::回顾如果使用整数, 其余部分可以作为一个小数写入 。

  

  播放段落

  When 729 is divided by 13, the remainder is 1 .  The quotient can be written as  $\begin{align*}56 +\tfrac{1}{13}=56 \tfrac{1}{13}.\end{align*}$  The divisor 13 can be taken out of 729 a total of 56 times,  with 1  leftover  out of 13.  You  can also think of this as  $\begin{align*}13 \cdot 56 + 1 = 729.\end{align*}$   The remainder of 1  means that 13 is not a factor of 729.
  ::当 729 除以 13 时, 其余部分为 1 。 商数可以写为 56+ 113= 56113。 13 位数可以从 729 中取出, 总共56 次, 其余 1 次, 13 次, 其余 1 次, 13 次, 13 次, 13 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 次, 3 5 5 +56+1 = 729 。 其余 1 次 表示 13 不 13 乘以 729 。

  播放段落

  Similarly, the remainder in polynomial division  can be written as a fraction over the divisor.
  ::同样,在多种族分隔法中,其余部分可以作为比分法的分数写成。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Divide  $\begin{align*}(x^4 + 4x^2 + 5x - 5) \div (x - 3)\end{align*}$
  ::除法 (x4+4x2+5x-5) (x-3)

  播放段落

  T ake a look at how dividing these two polynomials would play out. N otice that since the  $\begin{align*}x^3\end{align*}$   term is missing in the dividend, the term $\begin{align*}0x^3\end{align*}$  was added.
  ::看看这两个多面体会如何分化。 请注意, 由于股息中缺少 x3 术语, 增加了 0x3 术语 。

  

  播放段落

  Answer : $\begin{align*}x^3 + 3x^2 + 13x + 44 + \frac{127}{x-3}\end{align*}$  
  ::答复: x3+3x2+13x+44+127x-3

  播放段落

  This means that   $\begin{align*}(x-3)(x^3 + 3x^2 + 13x + 44) + 127 = x^4 + 4x^2 + 5x - 5.\end{align*}$  Since there  was a remainder  of 127,   $\begin{align*}x-3\end{align*}$  is not a factor of  $\begin{align*}x^4 + 4x^2 + 5x - 5.\end{align*}$
  ::这意味着(x-3)(x3+3x2+13x+44)+127=x4+4x2+5x-5。 由于其余127个, x-3不是 x4+4x2+5x-5的乘数。

  播放段落

  Note that w hen dividing polynomials, the remainder could be a number, as in the above example, or it could be a polynomial with a degree greater than 0.
  ::请注意,在分割多面体时,剩余部分可以是数字,如上例所示,也可以是一个多面体,度大于0。

  播放段落

  Now you can use polynomial division to  verify whether messages are corrupt. Keep in mind that a computer does long division in binary (base 2), compared to the normal base 10. Remember that if division  results in a remainder, then the information was corrupted.
  ::现在您可以使用多元分解来验证信件是否腐败。 请注意, 计算机在二进制( 基准 2) 中进行长的分解, 与正常的基数相比 10 。 记住, 如果分解导致剩余部分, 那么信息会被损坏 。

   

  播放段落

  Discussion Question : Are polynomials closed under division?
  ::讨论问题:多党制是否按分部关闭?

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

   

  ---

  播放段落

  Extension: Interactive Practice
  ::扩展:交互式做法

  播放段落

     Summary
  ::摘要

  播放段落
  • You can divide two polynomials using the  box method by working backward.
    ::您可以使用盒式方法向后工作来分割两个多面性。
  播放段落
  • You can also use the  long division algorithm: divide, multiply, subtract, bring down.
    ::您也可以使用长分割算法: 分隔、 乘法、 减法、 降法 。
  播放段落
  • Similar to  integers, polynomial division can result in a remainder .
    ::与整数相似,多数值分裂可能导致剩余部分。