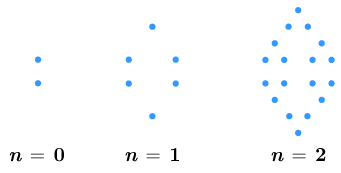5.2 指数函数-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节指数函数

  折叠 展开

  指数函数

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Understand the characteristics and structure of exponential functions.
    ::了解指数函数的特性和结构。
  播放段落
  • Find the domain and range of an exponential function .
    ::查找指数函数的域和范围。
  播放段落
  • Understand asymptotes .
    ::理解无症状。
  播放段落
  • Identify the effect on the graph of an exponential function after a transformation.
    ::识别转换后指数函数对图形的影响。
  播放段落
  • Understand the characteristics of growth and decay functions.
    ::了解生长和衰变功能的特征。
  播放段落
  • Solve problems involving and decay. 
    ::解决与腐烂和腐烂有关的问题。

  ---

  播放段落

  Introduction:  Going Viral
  ::一. 导言:动脉动动脉动

  

  播放段落

  Riley made a music video and released it. Here is a table  that displays the number of views each day:
  ::Riley制作了一个音乐视频, 并发行了它。 这是一张显示每天浏览次数的表格 :

  Day	Views
  1	5
  2	25
  3	125
  4	625
  5	3,125
  6	15,625

  播放段落

  At this rate , how long will it take for Riley's video to reach 1 million views? W rite a f unction to give you the number of views after d days.
  ::以这个速度, Riley 的视频需要多长时间才能达到100万次浏览? 写入一个函数, 给您在 D 天之后的浏览次数 。

   

  ---

  播放段落

  Activity 1:  Geometric Series
  ::活动1:几何系列

  播放段落

  The term viral gets its name because the  video, meme, or idea  spreads from person to person, much like a virus, increasing quickly and exponentially. Just as multiplication is a form of repeated addition , exponentiation is a form of repeated multiplication. Every day, the views for Riley's video increase by a product of 5.
  ::病毒一词之所以被命名,是因为视频、Meme或思想在人与人之间传播,就像病毒一样,快速和指数增长。 正如乘法是一种反复添加的形式一样,推论是一种反复倍增的形式。 每天 Riley的视频浏览量通过5的产物增加。

  

  播放段落

  T he differences in the outputs in a linear function are constant . Additionally,  the second differences of the outputs in  a quadratic function are constant and the third differences of the outputs in a cubic  function are constant. However, exponential functions increase and decrease  differently to polynomial functions .  T he exponential function above is the first glimpse at a geometric function. A geometric function is a function that increases by a common ratio.  You are multiplying to get from one term to the next rather than adding.
  ::线性函数中产出的差异是不变的。此外,二次函数中产出的第二个差异是恒定的,三次函数中产出的第三个差异是恒定的。然而,指数函数的增减与多元函数的增减是不同的。以上指数函数是几何函数的第一线。几何函数是一个以共同比率增加的函数。您正在从一个任期到下一个任期,而不是增加一个任期。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Use the pattern in the figures below to answer the following questions.
  ::使用下图中的模式回答下列问题。

  

  播放段落

  a.  H ow many dots will the  fourth figure in the sequence have? 
  ::a. 序列中的第四位数字将有多少点?

  播放段落

  M ake a table to help display the number of dots in each figure:
  ::制作一个表格,帮助显示每个图中点数 :

  播放段落

  $$\begin{align*}\begin{array}{| l | c | c | c | c |} \hline \text{Figure in the Sequence} & 1 & 2 & 3 & 4 \\  \hline \text{Number of Dots} & 2 & 6 & 18 & ? \\  \hline \end{array}\end{align*}$$
  ::Dots2618的序列1234数目?

  播放段落

  This pattern starts with 2 dots, and the number of dots in each figure increases the number of dots by a factor of 3. The next figure in the sequence will have  $\begin{align*}18 \cdot 3 \end{align*}$  dots.
  ::此模式以 2 点开始, 每个数字中的点数会将点数增加 3 系数 。 序列中的下一个数字将显示 18 3 点 。

  播放段落

  Answer:  The fourth figure will have 54 dots.
  ::答复:第四个数字将有54点。

  播放段落

  b. How many dots will the 10th figure in the sequence have?
  ::b. 序列中第10位数有多少点?

  播放段落

  To get to the second figure, start with 2 and multiply by 3 one time.
  ::要达到第二个数字,从2开始,再乘3一次。

  播放段落

  $$\begin{align*}\text{2nd term: } 2\cdot 3\end{align*}$$
  ::第二学期:第二学期:第二学期

  播放段落

  To get to the third figure, start with 2 and multiply by 3 two times.
  ::要达到第三个数字,从2开始乘以3乘以2乘以2乘以2乘以2乘以3乘以2乘以2。

  播放段落

  $$\begin{align*}\text{3rd term: } 2\cdot 3 \cdot3\end{align*}$$
  ::第3学期:233

  播放段落

  To get to the fourth figure, start with 2 and multiply by 3 three times.
  ::要达到第四位数字,从2开始乘以3乘以3乘以3乘以3乘以3乘以3。

  播放段落

  $$\begin{align*}\text{4th term: } 2\cdot 3 \cdot3 \cdot 3\end{align*}$$
  ::第4学期:2 3 3 3

  播放段落

  To get to the 10th figure, multiply 2 by 3 nine times. Instead of writing out nine 3's, you can write it as 3 to the ninth power.
  ::要达到第10位数,乘以2乘以3乘以3乘以9乘以9。你可以把它写成第9位数,而不是写成第9位数, 而不是写成第9位数的3。

  播放段落

  $$\begin{align*}\text{10th term: } 2 \cdot {3}^{9}\end{align*}$$
  ::第10学期:2____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Answer: The tenth figure will have 39,366 dots.
  ::答复:第十个数字将有39 366点。

  播放段落

  Answer the questions below to look for patterns in geometric sequences.
  ::回答下面的问题 寻找几何序列的图案

  ---

  播放段落

  Activity 2: Revisiting Exponential Functions
  ::活动2:重新审视指数函数

  播放段落

  An exponential function is a geometric function that takes the form  $\begin{align*}y=ab^x.\end{align*}$  The coefficient $\begin{align*}a\end{align*}$  is generally considered the starting amount in most contexts. In the example above, the video started with 1 person, but  there will be  many examples where the starting amount is a number other than 1. The variable $\begin{align*}b,\end{align*}$  the base, is often referred to as either the common ratio . This v alue represents the amount by which the starting amount is repeatedly multiplied. For all exponential functions, the value of $\begin{align*}b\end{align*}$   must be positive. The function modeled in the introduction is $\begin{align*}f(x) = 5^x.\end{align*}$   I nput-output pairs can be obtained for this function by substituting a value for the exponent , $\begin{align*}x,\end{align*}$   and solving for $\begin{align*}f(x).\end{align*}$   For example,  $\begin{align*}f(3) = 125\end{align*}$  because  $\begin{align*}{5}^{(3)}=125.\end{align*}$
  ::指数函数是一个以 y=abx 形式出现的几何函数。 系数a 通常被视为大多数情况下的起始量。 在以上示例中, 视频以 1 人开始, 但有很多例子显示起始数是 1 以外的数。 变量b 基数通常被称为 共同比率 。 这个数值代表起始数反复乘以的数。 对于所有指数函数, b 的值必须是正值。 在导言中建模的函数是 f(x)= 5x 。 通过替换 exponent, x 和 f(x) 的解析法, 可以获得用于此函数的输入输出对配方。 例如, f(3)=125, 因为 5(3)=125 。

  

  播放段落

  Discussion Question : Why will this function never equal to zero? Use the function $\begin{align*}y = 5^x\end{align*}$  and its graph to prove your answer.
  ::讨论问题:为什么这个函数永远不等于零?使用y=5x及其图表来证明您的回答。

  播放段落

  I n context, a video could have no views. However, the function  $\begin{align*}y=5^x\end{align*}$  will never have an output of zero. When a function approaches a value but never reaches it, this is called an asymptote .
  ::在上下文中, 视频可能没有视图 。 但是, y= 5x 函数永远不会输出为零 。 当函数接近一个值但从未到达它时, 这被称为“ 无时点 ” 。

  

  ---

  播放段落

  Activity 3: The Rice and Chessboard Problem
  ::活动3:稻米和棋盘问题

  播放段落

  The rice and chessboard problem, dating back to the 1200s, is o ne of the earliest and most famous examples of an exponential function. Use the interactive below to explore this problem.
  ::大米和棋盘问题可以追溯到1200年代,它是指数函数最早和最著名的例子之一。 使用下面的交互作用来探索这个问题。

  播放段落

  The amount of rice per each square in the example above can be modeled using the function $\begin{align*}f(x) = 2^x.\end{align*}$  In the context of the problem, the domain is all real numbers, and the range is the whole number powers of 2. However, expand this function beyond the confines of the context. Use the table below to  find  the coordinate pairs for the  relation $\begin{align*}y = 2^x.\end{align*}$    
  ::以上示例中每个方形的稻米量可以使用函数 f(x)=2x来模拟。在问题的背景下,域名是所有实际数字,范围是整个2的数权。然而,将这一函数扩大到上下文范围以外。使用下表来查找 y=2x 关系中的坐标对。

  播放段落

  Use the interactive below to graph the function formed by the table above, as well as two additional exponential functions.
  ::使用下面的交互作用来绘制上表所形成的函数,以及另外两个指数函数。

  ---

  播放段落

  Activity 4: Properties and Graphs of Exponential Functions
  ::活动 4: 指数函数的属性和图示

  播放段落

  Exponential functions can be transformed using the notation  $\begin{align*}f(x)=a \cdot b^{x-h}+k,\end{align*}$   where $\begin{align*}h\end{align*}$  and $\begin{align*}k\end{align*}$  more the function in the $\begin{align*}x\end{align*}$  and $\begin{align*}y\end{align*}$  directions, respectively. 
  ::指数函数可以使用 f(x) = abx-h+k的标记转换,其中 h 和 k 分别是 x 和 y 方向中的函数。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Modern music software contains programs that allow users to create music without instruments. This music is created by relating notes to their frequencies.  The frequencies of the notes on a  piano can be modeled using the following exponential equation  %20%3D%20440%20%5Ccdot%20%7B2%7D%5E%7B%5Cfrac%7B(n-9)%7D%7B12%7D%7D."> $\begin{align*}P(n) = 440 \cdot {2}^{\frac{(n-9)}{12}}.\end{align*}$  The variable n represents the notes in order such that  $\begin{align*}P(0)\end{align*}$  is middle C,  often referred to  as C4, and  $\begin{align*}P(1)\end{align*}$  is the next note in the order, C#. 
  ::现代音乐软件包含允许用户在没有乐器的情况下创作音乐的程序。 这种音乐是用与其频率相关的音符创建的。 钢琴上的音符频率可以用以下指数方程式P( n)=4402( n- 912)来模拟。 变量 n 代表音符, 以便P( 0) 是中间的C, 通常被称为C4, P(1) 是下一个音符的音符, C# 。

  

  播放段落

  Use a calculator or graphing software to help answer the questions below:
  ::使用计算器或图形化软件帮助回答下列问题:

  播放段落

  Discussion Question : Will all perfect fifths have the ratio 3:2? How do you know?
  ::讨论问题:所有五分之一的完美男女比例是否为3:2? 你怎么知道?

  播放段落

  In the formula above, t he number 440 is the starting frequency of A4, the A in the fourth octave. The $\begin{align*}b\end{align*}$  takes on the value 2 because this is the rate at which the frequency increases. The exponent modifies the starting note and the rate of increase. The exponent has a 9 subtracted from $\begin{align*}n\end{align*}$  to shift the function in the negative direction 9 units. Since each unit is a note, the nine shifts the starting note over to C4 while still keeping A4's frequency of 440. This shift is done because the frequency of A4 is a whole number, which is easy to work with, whereas the frequency of C4 is an irrational number. The 12 splits up the rate of increase over 12 notes. The frequencies double every 12 notes.
  ::在以上公式中, 440 是 A4 的起始频率, A 在四进制中的 A 。 b 取值 2, 原因是这是频率增加的速率 。 引言修改起始注和增长率 。 引言从 n 减9 , 将函数向负方向 9 单位转移。 由于每个单位都是注, 9 将起始注移到 C4 , 同时又保持 A4 的 440 个频率 。 此转换是因为 A4 的频率是一个完整数字, 这很容易操作, 而 C4 的频率是一个不合理的数字 。 12 将增加速度除以 12 个注。 频率每 12 倍翻一番 。

  ---

  播放段落

  Activity 5:  Half-Life
  ::活动5:半衰期

  播放段落

  Scientists use processes like carbon dating to determine the ages of ancient artifacts. As the elements that make up an artifact age they decay, release energy, and turn into other elements. For example, carbon-14 is an unstable radioactive isotope of carbon found in organic matter. As time advances, the carbon-14 isotopes release energy and turn into the stable isotope nitrogen-14. This process is called radioactive decay. The radioactive isotope, carbon-14, in this case, is referred to as the parent isotope, and the stable isotope, nitrogen-14, is referred to as the daughter isotope. C arbon-14 decays at an exponential rate  with a  half-life of about 5,7 0 0 years. I t is called a half-life   because,   after 5,700 years, approximately half of the carbon-14 isotopes will turn into nitrogen-14.   A fter another 5,700 years, half of the remaining carbon-14 isotopes will turn into nitrogen-14. 
  ::科学家使用诸如碳日期等过程来确定古代文物的年代。 作为构成文物时代的要素,他们衰减、释放能量并转化为其他元素。 例如,碳-14是有机物中发现的碳的不稳定放射性同位素。 随着时间的进步,碳-14同位素释放能量,并转化为稳定的同位素氮-14。这一过程被称为放射性衰减。放射性同位素,碳-14,在这里被称为母同位素,稳定的同位素,氮-14,被称为女同位素。碳-14以指数速度衰减,半衰期约为5,700年。它被称为半衰期,因为经过5,700年之后,大约一半的碳-14同位素将变成氮-14。再过5,700年之后,剩余的碳-14同位素的一半将变成氮-14。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  A fossil is found from a woolly mammoth   believed to be approximately 17,000 years old . A sample is taken for analysis. After 17,000 years, approximately what percentage of carbon should be left in the fossil sample?
  ::一种化石是从一只被认为大约17,000年的羊毛长毛象身上找到的。 采集了一个样本以供分析。 在17,000年之后,在化石样本中应该留下大约多少比例的碳?

  播放段落

  The mammoth would have consumed carbon-14 when it ate .  However, after   dying , no more carbon-14 would have been consumed, when the carbon-14 was at 100%. Every 5,700 years, the amount of carbon-14 is reduced by half. U se the following formula to answer this question:
  ::长毛象在食用时会消耗碳-14。 但是,在死后,当碳-14为100%时,碳-14将不再消耗碳-14。 每5,700年,碳-14的数量将减少一半。 使用以下公式回答这个问题:

  播放段落

  $$\begin{align*}\text{Percent Carbon-14 } = 100\cdot {\frac{1}{2}}^{\text{Number of Half-Lives}}\end{align*}$$
  ::碳-14百分比 = 10012

  播放段落

  The value of $\begin{align*}a\end{align*}$  in the formula is 100 because it started at 100%. The value of $\begin{align*}b\end{align*}$  in the formula is  $\begin{align*}\frac{1}{2}\end{align*}$  because every 5,700 years the percent of carbon-14 is reduced by half.
  ::公式中一个值为100, 因为它的起点是100%。 公式中 b 值为12, 因为每5700年碳-14 的百分率降低一半 。

  

  播放段落

  Since   $\begin{align*}5700 \cdot 3 = 17,100,\end{align*}$ approximately 3 half-lives would have passed if the fossil is 17,000 years old. By substituting 3 into the formula for the number of half-lives,  the following will be  obtained:
  ::自57003=17 100以来,如果化石的寿命为17 000年,大约3个半衰期会过去。通过将3个半衰期替换成半衰期的公式,将获得以下结果:

  播放段落

  $$\begin{align*}\text{Percent Carbon-14 } &= 100\cdot {\frac{1}{2}}^{3} \\\\&= 100\cdot\frac{1}{8} \\\\&= 12.5\end{align*}$$
  ::碳-14 = 100123 = 10018 = 12.5

  播放段落

  Answer:  A 17,000-year-old fossil would contain approximately 12.5% carbon-14.
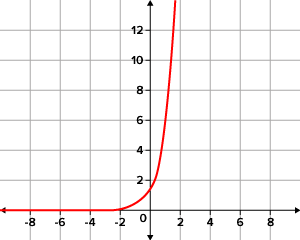
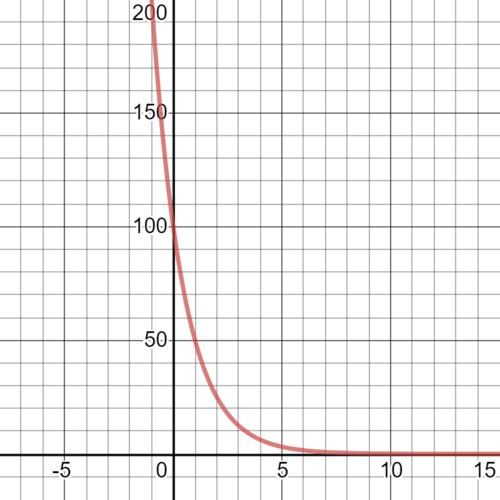
  ::答复:17 000年的化石含有大约12.5%的碳-14。

  播放段落

  When the output of an exponential function increases as the input increases,  it is called a   growth function. This type of function occurs when the value of $\begin{align*}b\end{align*}$   is greater than 1. When the output of an exponential function decreases as the input increases,  it is called a   decay function . This type of function occurs when the value of $\begin{align*}b\end{align*}$   is between 0 and 1.
  ::当一个指数函数的输出随着输入的增加而增加时,它被称为增长函数。当 b 值大于 1. 1 时,这种类型的函数发生。当一个指数函数的输出随着输入的增加而减少时,它被称为衰变函数。当 b 值介于 0 和 1 之间时,这种类型的函数发生于 b 值介于 0 和 1 之间时。

  播放段落

  Carbon dating works great for samples that are tens of thousands of years old, but what if a sample was 100 years old or 1,000,000 years old? Different radioactive isotopes are used for samples based on their age.
  ::对于数万年前的样本来说,碳的约会效果很好,但如果样本是100岁或100万年前的呢? 不同的放射性同位素根据其年龄用于样本。

  Isotope	Half-Life
  Uranium-238	4,500,000,000 years
  Plutonium-239	24,000 years
  Carbon-14	5,700 years
  Radium-226	1620 years
  Hydrogen-3	12  years
  Potassium-32	14 days

  播放段落

  Discussion Question : An analysis shows that a sample has 35% carbon-14. Estimate the age of the sample. Try to be as accurate as possible.
  ::讨论问题:分析显示样本有35%的碳-14。 估计样本的年龄。 请尽量准确 。

   

  ---

  播放段落

  Extension: Exponential Growth in Fractals
  ::扩展:分形指数增长

  播放段落

  Did you know that the same mathematical principle that is observed in snowflake patterns is used to design video game layouts? These patterns are called fractals. Use the interactive below to explore the link between fractals and exponential functions.
  ::您知道在雪花模式中观察到的同样的数学原理 用于设计视频游戏布局吗? 这些模式被称为分形。 使用下面的交互作用来探索分形和指数函数之间的联系 。

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

     Summary
  ::摘要

  播放段落
  • An exponential function is a geometric function that takes the form  $\begin{align*}y=ab^x,\end{align*}$  where the variable $\begin{align*}b\end{align*}$  is often referred to as the common ratio.
    ::指数函数是一个以 y=abx 形式出现的几何函数,变量b通常被称为共同比率。
  播放段落
  • When a function approaches a value but never reaches it, this is called an asymptote.
    ::当函数接近一个值但从未达到它时,它被称为“无时点”。
  播放段落
  • When the output of an exponential function increases as the input increases, it is called a growth function. This type of function occurs when the value of $\begin{align*}b\end{align*}$  is greater than 1. When the output of an exponential function decreases as the input increases, it is called a decay function. This type of function occurs when the value of $\begin{align*}b\end{align*}$  is between 0 and 1.
    ::当一个指数函数的输出随着输入的增加而增加时,它被称为增长函数。当 b 值大于 1. 1 时,这种类型的函数发生。当一个指数函数的输出随着输入的增加而减少时,它被称为衰变函数。当 b 值介于 0 和 1 之间时,这种类型的函数发生于 b 值介于 0 和 1 之间时。
  播放段落
  • The transformed exponential function is  $\begin{align*}f(x)=a\cdot b^{x-h}+k,\end{align*}$ where  $\begin{align*}h\end{align*}$  moves the function horizontally,  $\begin{align*}k\end{align*}$   moves the function vertically, and  $\begin{align*}a\end{align*}$  stretches or shrinks the function.
    ::变换的指数函数是 f( x) = abx-h+k, 其中 h 水平移动函数, k 垂直移动函数, 一个拉伸或缩缩函数 。