6.1 解决激进等号-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 解决激进等号

  Collapse Expand

  解决激进等号

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Solve simple radical equations in one variable .
    ::在一个变量中解决简单的激进方程式。
  播放段落
  • Give examples showing how extraneous solutions may arise.
    ::举例说明如何产生不相干的解决办法。

  ---

  播放段落

  Introduction: Speeding
  ::导言:加快速度

  

  播放段落

  Police  officers are always among the first on the scene of a car accident to offer help to anyone who may be injured. However, it is also the job of a police officer to figure out how the accident happened. There are many mathematical formulas and principles which come into play during this investigation. One formula uses the length of a skid mark to determine the speed of a car before the breaks were applied.
  ::警察总是在车祸现场首先向任何可能受伤的人提供帮助的警察之一,然而,警官也有责任查明事故是如何发生的,在这次调查中,有许多数学公式和原则发挥作用,其中一个公式使用滑雪标记的长度来确定汽车在使用休息前的速度。

  播放段落

  $$\begin{array}{r}s=\sqrt{2\cdot g\cdot L\cdot f}\end{array}$$

  
  ::=2gLf

  播放段落
  • $\begin{array}{r}s\end{array}$  is the speed of the vehicle in feet per second
    ::s 是每秒一英尺的车辆速度。
  播放段落
  • $\begin{array}{r}g\end{array}$  is the acceleration due to gravity,  $\begin{array}{r}32\text{ft}/{\text{s}}^2\end{array}$  
    ::g 指重力加速度,32英尺/秒2。
  播放段落
  • $\begin{array}{r}L\end{array}$  is the length of the skid mark in feet
    ::L 是脚底滑动标记的长度
  播放段落
  • $\begin{array}{r}f\end{array}$ is the coefficient of friction. Dry roads typically have a coefficient of friction of around 0.75, which will be assumed, but the more slippery a road gets the lower the coefficient friction. A wet road can have a coefficient of friction between 0.4 and 0.7.
    ::f 是摩擦系数。 干燥道路摩擦系数通常大约为0.75, 假设这一系数,但越滑道路摩擦越低。 湿道路摩擦系数可能介于0.4到0.7之间。

  播放段落

  The speed limit on a highway is 60 mph write an inequality to represent the potential skid mark lengths that a speeding car (traveling over 60 mph) could leave. What problems would arise from trying to write this inequality?
  ::高速公路的车速限制是60英里,这代表了超速车(行驶60英里以上)可能行驶的滑行长度。 试图写出这种不平等会产生什么问题?

   

  ---

  播放段落

  Activity 1: Understanding Radical Equations
  ::活动1:了解激进等

  播放段落

  Before solving the problem above, you will need to learn more about radical equations. In the chapter Polynomial Functions, you explored polynomial functions whose terms all have whole number degrees. This chapter will extend your knowledge beyond to terms with rational exponents. Recall from Revisiting Exponential Expressions that can be used to  represent   radicals . These basic exponent rules will be used to solve radical equations. You are likely familiar with the idea that square roots and squares are opposites. However, why are they opposites and how can this be applied to other roots?
  ::在解决上述问题之前, 您需要了解更多关于激进方程式的知识。 在“ 多边函数” 章节中, 您探索了多面函数, 其术语都具有全数度。 本章将把您的知识扩展至与理性推手的术语。 回想一下可以用来代表激进分子的重现实验表达式。 这些基本推理规则将用于解析激进方程式。 您可能熟悉平方根和正方形是相反的理念 。 但是, 为什么这些功能是相反的, 以及如何将其应用到其他根子上 ?

  播放段落

  Use the interactive below to answer these questions.
  ::用下面的交互方式回答这些问题。

   

   

  播放段落

  Discussion Questions :
  ::讨论问题:

  播放段落
  1. Why does raising both sides of an equation to a power maintain equality?
     ::为什么提出权力等式的两面都维持平等?
  播放段落
  2. When using the square root on both sides of an equation to cancel a squared variable, it results in a positive and negative solution. Why does   using the  cubed root on both sides of an equation to cancel a cubed variable only result in one solution? Generalize a rule for all whole numbers roots.
     ::当使用方程式两侧的平方根来取消一个平方变量时,它会产生正和负的解决方案。为什么使用方程式两侧的立方根来取消一个立方变量只产生一个解决方案?对所有数字根都普遍实行规则。
  播放段落
  3. Why doesn't  using a  square on both sides of an equation to cancel a square root  result in two solutions?  
     ::为何不使用方程式两侧的方块来取消方根,

   

  ---

  播放段落

  Extension: Visualizing Radicals
  ::扩展名: 可视化激进

  播放段落

  The following interactive enables you to geometrically visualize what a radical looks like.  
  ::下面的交互功能 使你能够从几何角度 直观地想象一个激进的外观。

   

  ---

  播放段落

  Activity 2:  Speeding Continued
  ::活动2:继续加快速度

  播放段落

  As you saw in the previous activity, an isolated exponent can be canceled by taking both sides of the equation to the reciprocal power. Since radicals are exponents, the same principle applies. U se the reciprocal of a fractional exponent to solve a basic radical problem and the problem from the introduction.
  ::正如您在前一次活动中看到的那样,一个孤立的指数可以通过将等式的两面都与对等权力相提并论的方式取消。 由于激进分子是推手,所以同样的原则适用。 使用一个分数的指数的对等法来解决一个基本激进问题和引言中的问题。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Solve  $\begin{array}{rl}3\sqrt[3]{x-8}-2& =\text{-}14\end{array}$  
  ::溶解 3x-83-2=14

  播放段落

  Solving radical equations is very similar to solving other types of equations. The objective is to get  x   by itself on one side of the equation.  Recall that the opposite operation of taking the square root of a value is squaring it.  In other words, if  $\begin{array}{r}\sqrt{x}=5\end{array}$ , then  $\begin{array}{r}{\left(\sqrt{x}\right)}^2=5^2,\text{ so }x=25.\end{array}$   To solve for   $\begin{array}{r}x\end{array}$ , f irst, isolate the radical on one side of the equation by  adding 2 to both sides and dividing by 3.
  ::解析激进方程式与解析其他方程式非常相似。 目标是让 x 自己在方程式的一边获得。 回顾取取一个值的平方根的相反操作正在对立它。 换句话说, 如果 x=5, 那么( x) 2=52, 所以 x=25。 要解析 x, 首先, 在方程式的一边隔离直方方方方程式, 向两边加2, 并除以 3 。

  播放段落

  $$\begin{array}{rl}3\sqrt[3]{x-8}-2& =\text{-}14\\ 3\sqrt[3]{x-8}& =\text{-}12\\ \sqrt[3]{x-8}& =\text{-}4\end{array}$$

  
  ::3-83-2=-143x-83=-12-83=-4

  播放段落

  Since  you now have a problem with a cubed root, to solve for   $\begin{array}{r}x\end{array}$   you need to   cube  both sides to eliminate the radical:
  ::既然您现在对立方根有问题, 要解决 x, 您需要立方两边才能消除激进 :

  播放段落

  $$\begin{array}{rl}{\left(\sqrt[3]{x-8}\right)}^3& =(\text{-}4{)}^3\\ {\left({\left(x-8\right)}^{\frac{1}{3}}\right)}^3& =(\text{-}4{)}^3\\ x-8& =\text{-}64\\ x& =\text{-}56\end{array}$$

  
  :x-833=(-4)3((x-8)133)3=(4)3x-8=-64x=-56)

  播放段落

  Answer:  $\begin{array}{r}-56\end{array}$  
  ::答复:-56

  播放段落

  Like with every equation , check your answer by substituting the answer in for the variable and checking to see if it makes the equation true.
  ::和每个方程式一样,检查你的答案,用变量的答案替换变量的答案,然后检查它是否使方程式真实。

  $$\begin{array}{r}3\sqrt[3]{\text{-}56-8}-2=\text{-}14\\ \\ 3\sqrt[3]{\text{-}64}-2=\text{-}14\\ \\ 3\cdot \text{-}4-2=\text{-}14\\ \\ \text{-}12-2=\text{-}14\end{array}$$

  播放段落

  The solution  $\begin{array}{r}x=\text{-}56\end{array}$  is correct.
  ::溶液 x=-56 正确 。

  播放段落

  U sing these strategies, it's time to revisit the question in the introduction.
  ::利用这些战略,现在是在导言中重新讨论这个问题的时候了。

  播放段落

  Example  
  ::示例示例示例示例

  播放段落

  The speed limit on a highway is 60 mph. Write an inequality to represent the potential skid mark lengths that a speeding car could leave. Use the formula  $\begin{array}{r}s=\sqrt{2\cdot g\cdot L\cdot f}\end{array}$  to help solve the problem.
  ::高速公路上的速度限值为60英里。 写入一个不平等的字, 以代表超速汽车可能离开的滑动标记长度。 使用公式 s=2gLf 来帮助解决问题 。

  播放段落

  You want to know what the length of a skid mark would be for a car traveling over 60 miles per hour. First, identify some variables:
  ::您想知道一辆每小时60英里以上的汽车滑行标记的长度。 首先,确定一些变量:

  播放段落
  • $\begin{array}{r}g=32{\text{ ft/s}}^2\end{array}$  
    ::g=32英尺/秒2
  播放段落
  • $\begin{array}{r}f=0.75\end{array}$  
    ::f=0.75

  播放段落

  You cannot use 60 miles per hour for $\begin{array}{r}s,\end{array}$ because the speed must be in feet per second.
  ::你不能用60英里每小时60英里的S, 因为速度必须以每秒每英尺的速度。

  播放段落

  $$\begin{array}{r}\frac{60\cancel{\text{miles}}}{1\cancel{\text{hour}}}\cdot \frac{1\cancel{\text{hour}}}{60\cancel{\text{minutes}}}\cdot \frac{1\cancel{\text{minute}}}{60\text{seconds}}\cdot \frac{5280\text{feet}}{1\cancel{\text{mile}}}=88\text{ ft/s}\end{array}$$

  
  ::60英里1小时1小时1小时60分钟1分钟1分钟5280英尺1英里=88英尺/秒

  播放段落

  The equation  $\begin{array}{r}88=\sqrt{2\cdot 32\cdot L\cdot 0.75}\end{array}$ will give the length of a skid mark produced by a car traveling at 88 feet per second. You could solve the equation first and then write  the answer as an inequality, but  in this case,  the relationship will be written and solved as an inequality.
  ::88=232L0.75的方程式将给出一辆每秒88英尺的汽车所生成的滑雪标记长度。 您可以首先解开方程式, 然后将答案写成不平等, 但在此情况下, 关系将被写成和解决为不平等 。

  播放段落

  $$\begin{array}{rl}88& <\sqrt{2\cdot 32\cdot L\cdot 0.75}\\ 88& <\sqrt{48L}\end{array}$$

  
  ::88 < 2-32L0.7588 < 48L

  播放段落

  If this was an expression , you would want to simplify the square root of 48. However, in this case that would be an unnecessary step.  B egin by taking the square of both sides since the radical is already isolated.
  ::如果这是一种表达方式,你会希望简化48的平方根。 但是,在这种情况下,这是一个不必要的步骤。 开始从双方的平方开始,因为激进分子已经是孤立的。

  播放段落

  $$\begin{array}{rl}{88}^2& <{\sqrt{48L}}^2\\ 7744& <48L\end{array}$$

  
  ::882<48L.2774<48L

  播放段落

  Lastly, divide both sides by 48.
  ::最后,将双方除以48。

  播放段落

  $$\begin{array}{rl}7744& <48L\\ ÷48& ÷48\\ 166\frac{1}{3}& <L\end{array}$$

  
  ::7744<48L484816613>

  播放段落

  Answer: A speeding car would  leave a skid mark longer than  $\begin{array}{r}166\frac{1}{3}\text{ ft}.\end{array}$
  ::回答:超速车辆留下的滑雪标记超过16613英尺。

  播放段落

  Use the interactive below to explore radical equations further.
  ::使用下面的交互方式来进一步探讨激进方程。

  

  INTERACTIVE

  Solving Radical Equations

  

  播放段落

  This interactive will generate random radical equations, and then demonstrate step-by-step solutions for them.
  ::这种互动将产生随机的激进方程式,然后为这些方程式展示逐步的解决办法。

  播放段落
  • Practice solving the equations by clicking the "Random Equation" button, and attempting to solve the equation on your own.
    ::练习解答方程式, 点击“ 调制方程式” 按钮, 并尝试自行解析方程式 。
  播放段落
  • Review the step-by-step solution and compare it to your own work to see how to improve your understanding of the process. 
    ::审查逐步解决的办法,并将其与你自己的工作进行比较,以便了解如何改善你对进程的理解。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

   

  播放段落

  Discussion Question : What is the solution to $\begin{array}{r}3\sqrt{x+3}+4=-11?\end{array}$ Check and explain your answer.
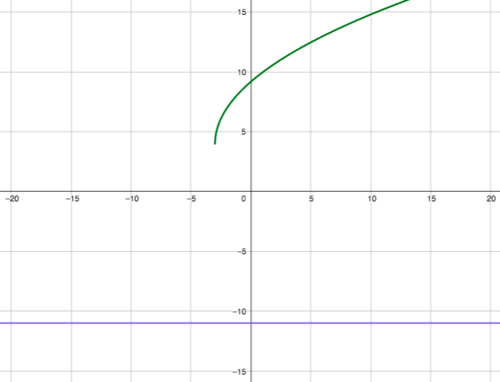
  ::讨论问题: 3x+3+4+11的解决方案是什么? 请检查并解释您的答复 。

   

  播放段落

  Here's a hint:
  ::这里有一个提示:

  

   

  ---

  播放段落

  Activity 3: Extraneous Solutions
  ::活动3:外部解决办法

  播放段落

  T ake the  following approach to  radical equations :
  ::对激进方程式采取以下方针:

  播放段落
  1. Isolate the radical.
     ::隔离激进分子
  播放段落
  2. Apply the inverse power to both sides of the equation.
     ::对方程的两侧应用反向力量。
  播放段落
  3. Solve the equation.
     ::解决这个方程式

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  $\begin{array}{r}x-3=\sqrt{x-1}\end{array}$
  ::x-3=x-1

  播放段落

  Since the radical is isolated, begin by squaring both sides.
  ::因为激进分子是孤立的,首先分裂双方。

  播放段落

  $$\begin{array}{rl}(x-3{)}^2& ={\sqrt{x-1}}^2\\ (x-3{)}^2& =x-1\end{array}$$

  
  :x-3)2=x-12(x-3)2=x-1

  播放段落

  When squaring both sides, you are not squaring each term ; you are squaring the entire expressions on both sides. In this case, you need to multiply out the binomial .
  ::当双方交替的时候,你们不是各定一个期限的;你们是双方全体的交替的。在这种情况下,你们要把两边的配角乘以两边的配角。

  播放段落

  $$\begin{array}{rl}(x-3{)}^2& =x-1\\ x^2-6x+9& =x-1\end{array}$$

  
  :x-3)2=x-1x2-6x+9=x-1

  播放段落

  Finally, solve the quadratic equation .
  ::最后,解开二次方程

  播放段落

  $$\begin{array}{rl}{x}^2-6x+9& =x-1\\ x^2-7x+10& =0\\ (x-2)(x-5)& =0\end{array}$$

  
  ::x2-6x+9=x-1x2-7x+10=0(x-2)(x-5)=0

  播放段落

  These factors represent the solutions to the quadratic equation: 2 and 5. However, are they the solutions to the radical equation?
  ::这些因素代表了二次等式的解决方案:2和5。 然而,它们是根本等式的解决方案吗?

  $$\begin{array}{rl}(2)-3& =\sqrt{(2)-1}\\ -1& =\sqrt{1}\\ -1& \ne 1\end{array}$$

  $$\begin{array}{rl}(5)-3& =\sqrt{(5)-1}\\ 2& =\sqrt{4}\\ 2& =2\end{array}$$

  播放段落

  Only 5 is a solution to the radical equation. Notice how the  value 2 produces a negative value outside the square root. Since a square root of a rational number will not produce a negative value, 2 cannot be the solution. A solution that does not satisfy the equation is called an extraneous solution . 
  ::只有5是激进方程式的解决方案。 注意值 2 在平方根外产生负值。 由于理性数字的平方根不会产生负值, 2 不能成为解决方案。 不符合等式的解决方案被称为不相干解决方案。

  播放段落

  Answer: 5
  ::答复:5

  Summary

  播放段落 To solve equations with radicals: 播放段落 Isolate the radical. ::隔离激进分子 播放段落 Apply the inverse power to both sides of the equation. ::对方程的两侧应用反向力量。 播放段落 Solve the equation. ::解决这个方程式 ::用激进方程式解析方程式: 隔离激进方程式。 对方程式的两侧应用反向力量。 解析方程式 。

  ---

  播放段落

  Wrap-Up: Review Questions 
  ::总结:审查问题