6.2 激进功能-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节激进函数函数函数

  折叠 展开

  激进函数函数函数

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • For a function that models a radical relationship between two quantities, interpret key features of graphs and tables in terms of the quantities.
    ::对于模拟两个数量之间的根本关系的函数,用数量来解释图表和表格的关键特征。
  播放段落
  • Sketch graphs showing key features of a radical relationship
    ::显示激进关系关键特征的 Spletch 图表
  播放段落
  • Identify the effect on the graph of a radical function replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative)
    ::以 f(x) + k、 kf(x)、 f(kx) 和 f(x + k) 替换 f(x) 和 f(x + k) k(正和负) 具体数值的基函数的图示效果

  ---

  播放段落

  Introduction: Tsunami
  ::导言:海啸

  播放段落

  A   t sunami is a series of massive waves caused by an earthquake, underwater volcanic eruption, or asteroid. Tsunamis can be catastrophic for anything that stands in their path. Giving the citizens of a community in the path of a tsunami enough time to get to high ground or as far inland as possible can save lives. Scientists estimate landfall time by calculating the speed of a tsunami based on the depth of the ocean and gravity. 
  ::海啸是地震、水下火山爆发或小行星造成的一系列大规模海啸。 海啸对于任何处于其道路上的人来说都可能是灾难性的。 给处于海啸道路上的社区公民足够的时间到达高地或尽可能远的内陆可以拯救生命。 科学家通过根据海洋深度和重力计算海啸速度来估计登陆时间。

  播放段落

  $$\begin{align*}s=\sqrt{g \cdot d}\end{align*}$$
  
  ::d

  播放段落
  • $\begin{align*}s\end{align*}$  is the speed of the wave in meters per second
    ::s 是每秒以米计的波速 。
  播放段落
  • $\begin{align*}g\end{align*}$  is the acceleration due to gravity, approximately  $\begin{align*}10 \: \text{m/s}^2\end{align*}$  
    ::g 指重力加速度,约10米/秒2。
  播放段落
  • $\begin{align*}d\end{align*}$  is the depth of the ocean in meters
    ::d 是海洋以米为单位的深度

  播放段落

  A cceleration due to gravity is relatively constant on Earth.  The value will be rounded from  $\begin{align*}9.8 \: \text{m/s}^2\end{align*}$   to $\begin{align*}10 \: \text{m/s}^2\end{align*}$  to make it easier to graph. T he  speed of the tsunami  can be written as a function of its distance from the shore using the function  $\begin{align*}s(d) = \sqrt{10 \cdot d}.\end{align*}$
  ::由于重力造成的加速度在地球上相对稳定。 数值将四舍五入, 从9. 8m/ s2到10m/ s2, 以便更容易绘制图表。 海啸的速度可以用函数 s( d)\\\\\ 10d, 以其距离海岸的函数函数来表示 。

  播放段落

  Use the interactive below to plot points based on input-output pairs.
  ::使用下面的交互功能,根据投入产出对等来绘制点。

  ---

  播放段落

  Activity 1: Radical Functions as Inverses of Polynomial Functions
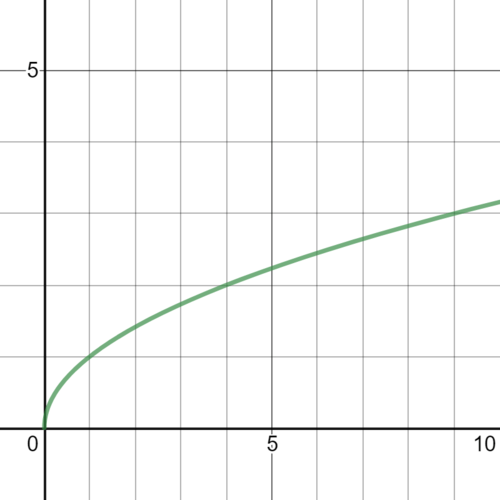
  ::活动1:作为多功能反面的激进函数

  播放段落

  The function above is an example of a radical function. The parent square root function is  $\begin{align*}y=\sqrt{x}.\end{align*}$  The graph of the function  $\begin{align*}y=\sqrt{x}\end{align*}$  can be seen below.
  ::以上函数是基函数的一个示例。父平方根函数为 yx。函数 yx 的图形见下文。

  

  播放段落

  Radical functions may seem less relevant than some of the functions  seen   thus  far. However, when you consider that radical functions are the inverse of polynomial functions, it is easier to see how relevant they are. In the section , you learned that the inverse of a function can be found by reflecting the function over the line formed by the function y = x. Use the interactive below to explore the relationship between quadratic and square root functions.
  ::激进函数可能似乎不如迄今为止所看到的一些函数那么重要。 但是, 当您认为激进函数是多元函数的反面时, 更容易看到它们的相关性。 在 一节中, 您了解到, 函数的反面可以通过反映函数 y = x 所构成的线上的函数来找到。 使用下面的交互功能来探索二次函数和平方根函数之间的关系 。

  播放段落

  Discussion Question : Generalize a rule for using the graph of $\begin{align*}y= x^n\end{align*}$  to graph $\begin{align*}y = x^{\frac1 n}.\end{align*}$  
  ::讨论问题:将y=xn图用于y=x1n图的规则普遍化。

   

  ---

  播放段落

  Activity 2: Using Graphs to Solve Radical Functions
  ::活动2:利用图表解决激进函数

  播放段落

  The discrepancy between the function  $\begin{align*}y = x^2\end{align*}$  and the inverse  $\begin{align*}y = \sqrt{x}\end{align*}$   is what causes extraneous solutions. In the section Solving Radical Equations,  you solved the equation  $\begin{align*}x-3=\sqrt{x-1}\end{align*}$  and found the answers 2 and 5. However,  after substituting 2 into the equation , you saw that it was extraneous. Another way to solve this equation is by graphing. G raph the function on the left  $\begin{align*}f(x) = x-3\end{align*}$  and the function on the right  $\begin{align*}g(x) = \sqrt{x-1}.\end{align*}$  The solution(s) will be the x-value of the intersection(s) of the functions. Use the interactive below to solve the equation by graphing .
  ::函数 y=x2 和 y =x 和 y =x 和 y =x 之间的差异是造成不相干解决方案的原因。在解析激进方程式部分,您解析了方程式 x-3x-1 并找到了答案 2 和 5 。然而,在将 2 替换为方程式后,您看到它不相干。解决此方程式的另一种方法是图形化。绘制左f(x) =x-3 的函数和右g(x) x- 1 的函数。解决方案将是函数的交叉点的 x 值。使用下面的交互式方法通过图形化解析方程式。

  播放段落
  • Given the graph above and your knowledge of inverse functions, what do you think causes extraneous solutions?
    ::考虑到上面的图表和您对反函数的了解, 你认为什么导致不相干的解决办法?

  播放段落

  Use the interactive below to explore graphs of radical functions further.
  ::使用以下互动方式进一步探讨激进函数的图表。

  播放段落

  Discussion Question : What does the graph of $\begin{align*}y = {x}^{2/3}\end{align*}$  look like? Explain why it takes this form.
  ::讨论问题:y=x2/3的图象是什么?解释为什么它采取这种形式。

   

  ---

  播放段落

  Activity 3: Transformations of Radical Functions
  ::活动3:激进职能的转变

  播放段落

  Transformations help fit radical models to a wide range of scenarios. The general parent radical function can be transformed as follows:
  ::转变有助于使激进模式适应各种情况。

  播放段落

  $\begin{align*}y = a\sqrt[n]{x-h}+k\end{align*}$
  ::y=an_x_h+k y=an_x_h+k y=an_h+k

  播放段落
  • $\begin{align*}n\end{align*}$  is the root
    ::n 是根
  播放段落
  • $\begin{align*}a\end{align*}$ will stretch or shrink the function vertically .
    ::a 将垂直拉伸或缩缩函数。
  播放段落
  • $\begin{align*}h\end{align*}$  will shift the function from left to right.
    ::h 将函数从左向右移动。
  播放段落
  • $\begin{align*}k\end{align*}$  will shift the function up and down.
    ::k 将函数向上或向下移动 。

  播放段落

  Use the interactive below to explore transformations of the parent square root function  $\begin{align*}y=\sqrt{x}.\end{align*}$
  ::使用下面的互动来探索父平方根函数 yx 的转换。

  ---

  播放段落

  Activity 4: Modeling with Radical Functions      
  ::活动4:与激进功能建模

  播放段落

  Another common use of radical functions is to model geometric relationships. Squares and cubes are used to model area and volume respectively. Square roots and cubic roots are necessary to model a two or three-dimensional relationship in terms of 1-dimension. 
  ::基函数的另一个常见用途是建模几何关系。 方块和立方体分别用于建模面积和体积。 平方根和立方根对于建模一维或三维关系是必要的。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Write a function that models the volume of a sphere as a function of the radius.
  ::写入函数,将球体的体积作为半径的函数来模拟。

  播放段落

  The formula  $\begin{align*}V = \frac{4}{3}\pi r^3\end{align*}$ can be used to find the volume of a sphere based on the radius. Write volume as a function of the radius by solving for the radius. 
  ::V=43°r3 公式可用于查找基于半径的球体体积。通过解析半径,将音量作为半径的函数写入。

  播放段落

  $$\begin{align*}V \:\:&= \frac{4}{3} \pi r^3\\ \div \frac{4}{3} \pi &\:\div \frac{4}{3} \pi \\ \hline \frac{3V}{4 \pi} &= r^3\end{align*}$$
  ::V=43r343433V4r3

  播放段落

  To move the exponent , use the third root.
  ::要移动引号, 请使用第三个 root 。

  播放段落

  $$\begin{align*}\sqrt[3]{\frac{3V}{4 \pi}} &= \sqrt[3]{{r^3}}\\\\ \sqrt[3]{\frac{3V}{4 \pi}}&= r\end{align*}$$
  ::333333334r

  播放段落

  Answer the questions  below to write radical functions for the geometric scenarios presented.
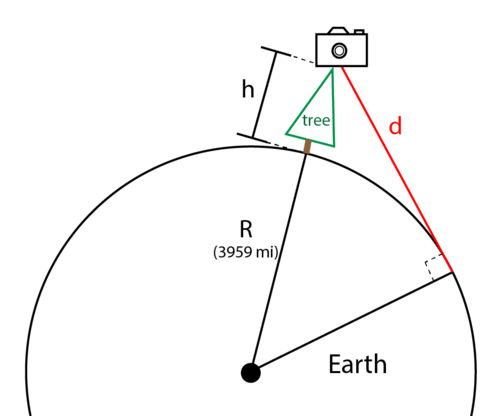
  ::回答下面的问题,为所提出的几何假设情景写出基本功能。

  播放段落

  Discussion Question :   T he function %20%3D%201.22%5Csqrt%7Bh%7D"> $\begin{align*}d(h) = 1.22\sqrt{h}\end{align*}$  is used to estimate the distance, in miles , you can see into the horizon from a height of $\begin{align*}h\end{align*}$   feet .
  ::讨论问题:函数d=1.22h用于估计距离,以英里计,从h英尺高处可以看到地平线。

  播放段落

  Imagine a camera at the top of a very tall tree, how far into the distance could it picture before the curve of the earth blocked the view? Use the image below to help derive the function that describes the view distance as a function of the height of the tree.
  ::想象一棵高树顶部的相机, 它在地球曲线挡住视图之前能画出距离有多远? 使用下面的图像来帮助产生函数, 该函数将视距描述为树高的函数 。

  

  Summary

  播放段落 Radical functions are inverses of polynomial functions ::激进函数是多元函数的反函数 播放段落 The general parent radical function can be transformed as follows: $$\begin{align*}y= a\sqrt[n]{x - h }+ k\end{align*}$$ 播放段落 $\begin{align*}n\end{align*}$  is the root ::n 是根 播放段落 $\begin{align*}a\end{align*}$  will stretch or shrink the function horizontally. ::a 水平拉伸或缩缩函数。 播放段落 $\begin{align*}h\end{align*}$  will shift the function from left to right. ::h 将函数从左向右移动。 播放段落 $\begin{align*}k\end{align*}$  will shift the function up and down. ::k 将函数向上或向下移动 。 ::一般父基函数可转换如下: y=an_x_h+k n 是函数的根, 将水平拉伸或缩缩。 h 将把函数从左向右。 k 将函数向上或向下移动 。

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题