课程： 6.3 合理函数-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

理性函数

Lesson Objectives
::经验教训目标

For a function that models a rational relationship between two quantities, interpret key features of graphs and tables in terms of the quantities .
::用于模拟两个数量之间合理关系的函数,按数量解释图表和表格的关键特征。

Sketch graphs showing key features of a rational function .
::显示合理函数关键特征的 Slich 图表。

Simplify rational expressions to identify holes in the domain of a function.
::简化合理表达式,以识别函数域中的空洞。

Introduction: Bright Lights
::导言:亮光

Th us far, you have explored graphs of functions in the form of $\begin{aligned} x^{n} \end{aligned}$ where n is a positive rational number . The next step is exploring functions in the same form where $\begin{aligned} n \end{aligned}$ is negative. These functions are known as rational functions. Rational functions are based on a similar idea to rational numbers. A rational number is a number that can be written as a ratio of two integers . A rational function is a function that can be expressed as a ratio of two polynomial functions. Rational functions can be written as $\begin{aligned} r (x) = \frac{f (x)}{g (x)} \end{aligned}$ where $\begin{aligned} f (x) and g (x) \end{aligned}$ are polynomial functions.
::到目前为止,您已经以 xn 的形式探索了函数图, n 是正理性数。下一步是以相同形式探索函数, n 是负函数。这些函数被称为理性函数。理性函数基于与合理数字相似的理念。一个合理数值是一个可以写成为两个整数之比的数字。一个合理函数是一个函数, 可以以两个多圆函数之比表示。理性函数可以写成 r( x)=f( x)g( x), f(x) 和 g(x) 是多元函数。

Thus far, you have learned the following:
::到目前为止,你们学到了以下知识:

are used to describe a proportional relationship.
::用于描述比例关系。

Polynomial functions are used to describe a power-based relationship.
::多面函数用来描述一种以权力为基础的关系。

Exponential and radical functions are used to describe a relationship that increases or decreases exponentially .
::指数函数和激进函数用来描述一种成倍增减的关系。

Rational functions are commonly used to describe an inverse relationship. An inverse relationship is a relationship such that when one value gets larger, the other value gets proportionally smaller and vice verse. One example of this is the brightness of a light. Use the interactive below to explore this relationship.
::理性函数通常用来描述反向关系。反向关系是一种关系,当一个值变大时,另一个值则成比例变小,反之则成比例变小。其中一个例子就是光的亮度。使用下面的交互式关系来探索这种关系。

INTERACTIVE

Light Bulb Representation of Rational Functions

Move the point on the slider to move closer to and further from a lightbulb.

::移动滑动器上的点,使滑动器的灯泡更近更近。

Activity 1: Understanding Rational Functions
::活动1:了解合理职能

The example above derives from the reciprocal function. Below is the reciprocal parent function.
::上述例子来自对等职能,以下是对等父母职能。

\begin{aligned} f (x) = \frac{1}{x} \end{aligned}

xx)=1x

A nalyze how this function would look on a graph. To help with this analysis, give the function a simple context. The formula $\begin{aligned} speed = \frac{distance}{time} \end{aligned}$ models the distance traveled by an object as a function of time. A ssume that you need to travel a distance of 1 mile. Average speed as a function of the time it took to travel that mile, in hours, can be written as follows :
::分析此函数如何在图形中查看。为了帮助进行此分析,请给此函数一个简单的上下文。公式速度=距离时间模型,一个对象所穿越的距离是时间的函数。假设您需要旅行1英里的距离。平均速度作为该里程所花费时间的函数,以小时计,可以写成如下:

\begin{aligned} s (t) = \frac{1}{t} \end{aligned}

::s(t)=1吨

Use the interactive below to find and plot the various average speeds you could travel per mile based on the time it took to travel 1 mile: (time, speed).
::使用下面的交互方式查找和绘制您根据行走1英里所需时间(时间、速度)每英里可以穿行的平均速度。

INTERACTIVE

Understanding Rational Functions

Use the table of given input values and calculate the output of the function $S\left(t\right)=\frac{1}{t}$ .
::使用给定输入值的表格,计算函数S(t)=1t的输出。

Input decimal numbers rounded to the nearest hundredth.
::输入小数位数四舍五入到最接近的百位数。

Discussion Question : The $\begin{aligned} y - \end{aligned}$ intercept can be found at $\begin{aligned} s (0) . \end{aligned}$ What would your speed be if you traveled $\begin{aligned} d \end{aligned}$ miles in 0 hours? What would this mean in the context of the problem?
::讨论问题:在 s(0) 中可以找到y interview 。如果您在 0 小时内行驶 d 英里, 您的速度会如何 ? 这在问题的背景中意味着什么 ?

Activity 2: Graphing Rational Functions
::活动2:绘制合理函数图

Now that you have explored a basic application of a rational function, it's time to expand your knowledge. In the interactive above the function $\begin{aligned} s (t) = \frac{1}{t} \end{aligned}$ is used to provide context for the function $\begin{aligned} f (x) = \frac{1}{x} . \end{aligned}$ Use the interactive below to graph $\begin{aligned} f (x) \end{aligned}$ when $\begin{aligned} x \end{aligned}$ is negative.
::既然您已经探索了理性函数的基本应用, 现在是时候扩展您的知识了。在 s( t) =1t 上方的交互函数中, 用于提供 f( x) =1x 函数的上下文。当 x 为负时, 请使用下面的交互效果来图f( x) 。

INTERACTIVE

Graphing Rational Functions

Use the table of given input values and calculate the output of the function $S\left(t\right)=\frac{1}{t}.$
::使用给定输入值的表格计算函数S(t)=1t的输出。

Input decimal numbers rounded to the nearest hundredth.
::输入小数位数四舍五入到最接近的百位数。

An asymptote is a value which a function gets closer to but never actually reaches. The rational function above has a vertical and a horizontal asymptote . A vertical asymptote is an input value which the function approaches but never reaches as $\begin{aligned} f (x) \end{aligned}$ increases or decreases without bound. A horizontal asymptote is an output value which $\begin{aligned} f (x) \end{aligned}$ approaches but never reaches as $\begin{aligned} x \end{aligned}$ increases or decreases without bound.
::空点是一个函数接近但从未实际达到的值。上面的理性函数有一个垂直和水平的空点。垂直空点是一个输入值, 该函数会接近, 但从未达到 f( x) 增加或减少而没有约束的输入值。水平静点是一个输出值, f( x) 接近, 但从未达到 x 增加或减少而没有约束的输出值。

Discussion Question : Why isn't 0 in the domain of $\begin{aligned} f (x) = \frac{1}{x} ? \end{aligned}$ Why isn't 0 in the range of $\begin{aligned} f (x) = \frac{1}{x} ? \end{aligned}$
::讨论问题:为什么在 f(x) = 1x 的域内不是 0 ? 为什么 0 在 f(x) = 1x 的域内不是 0 ?

Activity 3: Simplifying Rational Expressions
::活动3:简化理性表达式

Much like a rational number, a rational expression can be simplified. Thus far, you have been simplifying fractions like the ones in the interactive below.
::和理性数字一样,理性的表达方式可以简化。到目前为止,你一直在简化像下面互动中的分数一样的分数。

INTERACTIVE

Simplify Variable Expressions with Multiplication and Division

When dividing like terms, you can use the commutative and associative properties of division to group and simplify the coefficients and variables separately.
::当像用词一样的分隔时,您可以使用除法的通和和关联属性来分组和分别简化系数和变量。

Slide the colored points at the left of each expression to change the colored values.
::将每个表达式左侧的彩色点幻灯片,以更改彩色值。

See how changing the coefficients and powers of variables changes how the expressions are simplified.
::看看变数的系数和功率的变化如何改变表达式的简化。

R ational expressions can be simplified using the same approach:
::理性表达式可以采用同样的方法简化:

Factor the numerator and denominator.
::乘以分子和分母。

Cancel any common factors.
::取消任何共同因素。

Example
::示例示例示例示例

Simplify the rational function $\begin{aligned} f (x) = \frac{6 x^{2} - 12 x}{3 x^{2} - 3 x - 6} \end{aligned}$
::简化合理的函数 f( x) = 6x2 - 12x3x2 - 3x- 6

1. Factor the numerator and denominator.
::1. 乘以分子和分母。

\begin{aligned} \frac{6 x^{2} - 12 x}{3 x^{2} - 3 x - 6} = \frac{6 x (x - 2)}{3 (x^{2} - x - 2)} = \frac{6 x (x - 2)}{3 (x - 2) (x + 1)} \end{aligned}

::6x2 - 12x3x2 - 3x - 6= 6x(x-2) 3(x2-x-2) 3(x2-x-2) 6x(x-2) 3(x-2)(x+1)

2. Cancel any common factors.
::2. 取消任何共同因素。

\begin{aligned} \frac{26 x (x - 2)}{3 (x - 2) (x + 1)} = \frac{2 x}{x + 1} \end{aligned}

::26x(xx-2)3(x-2)(x+1)=2xx+1

Answer: $\begin{aligned} \frac{2 x}{x + 1} \end{aligned}$
::答复:2xx+1

Use the interactive below to practice .
::使用下面的交互操作。

Activity 4: Holes
::活动4:洞洞

When simplifying a fraction , the value of the fraction doesn't change. When simplifying a rational expression, there may be a change to the domain of the graph.
::当简化一个分数时, 分数的值不会改变。当简化一个合理的表达式时, 图形的域可能会有变化。

C onsider the two functions below:
::考虑以下两项职能:

\begin{aligned} f (x) = \frac{6 x^{2} - 12 x}{3 x^{2} - 3 x - 6} and g (x) = \frac{2 x}{x + 1} \end{aligned}

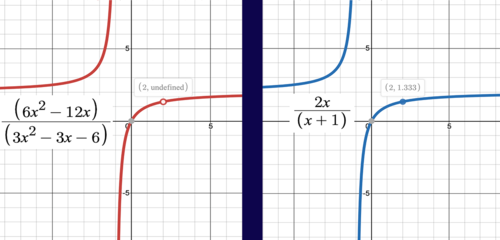
x) = 6x2 - 12x3x2 - 3x6 和 g(x) = 2xx+1

S tart by simplifying the function $\begin{aligned} f (x) . \end{aligned}$ Factoring the function reveals a common factor that can be canceled:
::通过简化函数 f(x) 开始。计算函数时会显示一个可以取消的共同系数 :

\begin{aligned} f (x) & = \frac{6 x (x - 2)}{3 (x - 2) (x + 1)} \\ f (x) & = \frac{6 x (x - 2)}{3 (x - 2) (x + 1)} \\ f (x) & = \frac{6 x}{3 (x + 1)} \\ f (x) & = \frac{3 (2 x)}{3 (x + 1)} \\ f (x) & = \frac{2 x}{x + 1} \end{aligned}

::f( x) = 6x( x-2) 3( x-2) 3( x) = 6x( x-2) 3( x-2) 3( x-2)( x+1) f( x) = 6x3( x) 3( x) 3( 2x) 3( x) 3( x+1) f( x) = 2xx+1

Since the function $\begin{aligned} g (x) \end{aligned}$ is the simplified from $\begin{aligned} f (x), \end{aligned}$ both graphs are relatively similar. Remember from above that any function can be graphed by plotting points. Since both functions are equivalent, each input should produce the same output. However, when plotting $\begin{aligned} f (2) and g (2), \end{aligned}$ you can see this isn't the case.
::由于函数 g( x) 是 f( x) 的简化格式, 两个图形相对相似。请从上面记住, 任何函数都可以用绘图点绘制图表。由于两个函数相同, 每个输入应产生相同的输出。但是, 在绘制 f(2) 和 g(2) 时, 您可以看到情况并非如此。

\begin{aligned} f (2) & = \frac{6 x^{2} - 12 x}{3 x^{2} - 3 x - 6} \\ = \frac{6 (2)^{2} - 12 (2)}{3 (2)^{2} - 3 (2) - 6} \\ = \frac{6 \cdot 4 - 12 (2)}{3 \cdot 4 - 3 (2) - 6} \\ = \frac{24 - 24}{12 - 6 - 6} \\ = \frac{0}{0} \end{aligned}

\begin{aligned} g (2) & = \frac{2 (2)}{(2) + 1} \\ = \frac{4}{3} \end{aligned}

A n input value of 2 makes the original function undefined but produces an output in the simplified function. When factoring the original function $\begin{aligned} f (x), \end{aligned}$ $\begin{aligned} (x - 2) \end{aligned}$ was a common factor in the numerator and denominator. Since plugging 2 into $\begin{aligned} (x - 2) \end{aligned}$ results in 0, an input value of 2 into $\begin{aligned} f (x) \end{aligned}$ results in $\begin{aligned} \frac{0}{0} \end{aligned}$ creating a hole in the graph at the point $\begin{aligned} (2, \frac{4}{3}) . \end{aligned}$
::2 的输入值使原始函数未定义,但在简化函数中产生输出。当将原始函数 f(x), (x)-2 乘以系数 f(x) 和分母是分子和分母的一个共同系数时。从将 2 插入 (x) 2 到 f(x) 的结果为 0, 输入值为 2 到 f(x) 的结果为 00 在点(2, 43) 在图形中创建空洞。

In general, an input that results in $\begin{aligned} \frac{0}{0} \end{aligned}$ is called a hole . To graph a function with a hole, graph the simplified function as you would normally but use an open circle at the location of the hole. Below is a graph of each function.
::一般而言,产生于00时的输入称为空洞。要用空洞绘制函数图,请按您通常的用法绘制简化函数图,但在空洞的位置使用一个开放圆。下面是每个函数的图形。

Use the interactive below to practice simplifying rational expressions and identifying holes.
::使用下面的交互式文字来简化合理表达方式,并找出漏洞。

Discussion Question : Could simplifying a rational function be used to make polynomial long division easier?
::讨论问题:能否利用简化合理职能,使多族裔长分界线更容易化?

Summary

A rational function is a function that can be expressed as a ratio of two polynomial functions.
::合理函数是一种可表述为两个多功能之比的函数。

Rational functions can be written as $\begin{aligned} r (x) = \frac{f (x)}{g (x)} \end{aligned}$
::有理函数可以写入 r( x) =f( x) g( x) 。

Rational functions are commonly used to describe an inverse relationship.
::理性函数通常用来描述反向关系。

An asymptote is a value which a function gets closer to but never actually reaches.
::无时点是一个函数接近但从未实际达到的值。

章节大纲

常规

理性函数

Introduction: Bright Lights ::导言:亮光

Activity 1: Understanding Rational Functions ::活动1:了解合理职能

Activity 2: Graphing Rational Functions ::活动2:绘制合理函数图

Activity 3: Simplifying Rational Expressions ::活动3:简化理性表达式

Activity 4: Holes ::活动4:洞洞

Wrap-Up: Review Questions ::总结:审查问题

Introduction: Bright Lights
::导言:亮光

Activity 1: Understanding Rational Functions
::活动1:了解合理职能

Activity 2: Graphing Rational Functions
::活动2:绘制合理函数图

Activity 3: Simplifying Rational Expressions
::活动3:简化理性表达式

Activity 4: Holes
::活动4:洞洞

Wrap-Up: Review Questions
::总结:审查问题