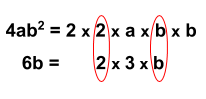6.6 增加和减法合理表达式-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 添加和减减理性表达式

  Collapse Expand

  添加和减减理性表达式

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Find the least common multiple of two or more polynomial expressions.
    ::查找两个或多个多多边表达式的最不常见的倍数。
  播放段落
  • Understand that rational expressions form a system analogous to the rational numbers, closed under addition  and  subtraction by a nonzero rational expression .
    ::理解理性表达方式形成一个类似于理性数字的体系,在增加和减以非零合理表达方式下封闭。
  播放段落
  • Add  and subtract rational expressions.
    ::添加和减去理性表达式。

  ---

  播放段落

  Introduction: The Harmonic Mean
  ::导言: 调和中

  播放段落

  The 16th-century architect Andrea Palladio used his love for music to guide his architectural designs. M usic notes run along an exponential scale. Notes create harmony if the ratios of their frequencies simplify to a simple ratio like 1:2, 2:3, etc.  Palladio believed that the design of a room should be harmonious. To create a  harmony between the length, with, and height of a room , he used the harmonic mean. The harmonic mean is a measure of center that dates back to ancient Greece.
  ::十六世纪的建筑师Andrea Palladio用他对音乐的热爱来指导他的建筑设计。音乐音符沿着指数尺度运行。如果音符的频率比简化到1:2:2:3等简单比例,音符就会创造和谐。 Palladio认为房间的设计应该和谐。为了在房间的长度、与房间的高度和高度之间创造和谐,他使用了口音的中枢。口音是可追溯到古希腊的中枢。

  播放段落

  The idea behind the harmonic mean of two numbers, call them a and b, is that both numbers are the same ratio from the harmonic mean.  Palladio would apply three numbers to the length, width, or height of a room or design. For example, if the a = 6 and b = 12, the harmonic mean would be 8. The harmonic mean 8 is one-third of 6 away from 6 and one-third of 12 away from 12.
  ::两个数字的调和平均值背后的想法是,两个数字与调和平均值的比重相同。 Palladio对一个房间或设计的长度、宽度或高度应用三个数字。例如,如果a=6和b=12,则调和平均值为8。 调和平均值8是6的三分之一,6是6的三分之一,12的三分之一。

  • $\begin{align*}\frac{1}{3}\cdot6 = 2 \rightarrow 6 + 2 = 8\end{align*}$  
  • $\begin{align*}\frac{1}{3}\cdot12 = 4 \rightarrow 12 - 4 = 8\end{align*}$  

  播放段落

  There are several formulas for the harmonic mean, but one of the more commonly accepted definitions is the following:
  ::口音平均值有几种公式,但最普遍接受的定义之一是:

  播放段落

  $$\begin{align*}\text{The harmonic mean of a and b}=\frac{2}{\frac{1}{a}+\frac{1}{b}}\end{align*}$$
  ::a 和 b= 21a+1b 的口音平均值

  播放段落

  This formula can be written more simply but to do so you will need to learn how to add rational expressions. The harmonic mean is also used outside of architecture to find P/E ratio (Price/Earning Ratio) in business, compare weighted rates, design traffic flow patterns, and is used in electrical circuit design.
  ::此公式可以写得更简单, 但这样你就需要学习如何添加理性表达方式。 调和平均值也用于建筑外, 在商业中找到 P/ E 比率( Price/ Earning 比率 ) , 比较加权比率, 设计流量模式, 并用于电路设计 。

   

  ---

  播放段落

  Activity 1: Least Common Denominator
  ::活动1:最不常见

  播放段落

  To understand the harmonic mean formula, focus on the denominator:
  ::为了理解和谐平均公式, 关注分母 :

  播放段落

  $$\begin{align*}\frac{1}{a}+\frac{1}{b}\end{align*}$$  
  ::1a+1b

  播放段落

  The denominator is a simple example of the sum of two rational expressions. To understand the process for adding these together,  you will need to revisit how fractions with whole number numerators and denominators are added.
  ::分母是两个合理表达式之和的简单示例。 要理解将这些表达式加在一起的过程, 您需要重新审视如何添加含有整数数数和分母的分数 。

   

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Add  $\begin{align*}\frac{4}{15} + \frac{5}{18}.\end{align*}$
  ::添加415+518。

  播放段落

  This problem requires you to add two fractions with different denominators; finding t he l owest c ommon d enominator (LCD) will be helpful. The LCD can be found by factoring the denominators: $\begin{align*}15=3 \cdot 5\end{align*}$ and $\begin{align*}18=3 \cdot 6\end{align*}$  which have a common factor of 3.
  ::这个问题要求您添加两个分数, 分母不同; 找到最小公分母( LCD) 会有帮助 。 通过对分母: 15= 3= 5 和 18= 3= 6( 共因数为 3) 进行乘法, 可以找到 LCD 。

  播放段落

  The LCD of two factored expressions includes each factor that appears in either expression , but common factors are only included once. In this example, that means the LCD includes 3, 5, and 6, so the LCD of 15 and 18 is $\begin{align*}(3)(5)(6) = 90.\end{align*}$   M ultiplying  each fraction ,   $\begin{align*}\tfrac{4}{15}\end{align*}$  and $\begin{align*}\tfrac{5}{18},\end{align*}$  by a fraction containing the missing factors from the denominator that is equivalent to 1 will result in a new fraction with a denominator of 90.
  ::两个因子表达式的LCD包括两种表达式中出现的每个因素,但共同因素只包括一次。在这个例子中,这意味着LCD包括3、5和6,因此15和18的LCD是(3)(5)(6)=90。乘以每个分数,415和518,再乘以一个分数,内含分数中缺失的分数,相当于1分数,将产生一个新的分数,分数为90分数。

  $$\begin{align*}\frac{4}{15} \cdot \frac{6}{6} = \frac{24}{90}\\ \ \\ \frac{5}{18} \cdot \frac{5}{5} = \frac{25}{90}\end{align*}$$

  播放段落

  T his logic is applied to rational expressions, using their factors to find the least common multiple .
  ::这一逻辑适用于理性表达方式,利用它们的因素来找到最不常见的多重。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Find the  least common multiple of the following:
  ::查找以下各项中最不常见的倍数 :

  播放段落
  1. $\begin{align*}4ab^2\end{align*}$   and $\begin{align*}6b\end{align*}$  
     ::4ab2和6b
  播放段落
  2. $\begin{align*}x^2 + 5x - 14\end{align*}$   and $\begin{align*}2x-4\end{align*}$  
     ::x2+5x-14和2x-4

  播放段落

  a. To find the LCM of  $\begin{align*}4ab^2\end{align*}$   and $\begin{align*}6b,\end{align*}$  first factor each expression.
  ::a. 找到4ab2和6b的 LCM,首先考虑每个表达式。

  播放段落

    •   $\begin{align*}4ab^2 = 2 \cdot 2 \cdot a \cdot b \cdot b\end{align*}$
  ::• 4ab2=2

  播放段落

    •   $\begin{align*}6b = 2 \cdot 3 \cdot b\end{align*}$
  ::• 6b=23b

  播放段落

  Although a and b could potentially factor further depending on the value inserted for a and b, since that value is variable and you do not know it, assume these expressions cannot be factored further. The  LCM will be the product of the common factors and the remaining factors.
  ::虽然a和b可能进一步根据a和b的插入值而进一步考虑,但由于该值是可变的,而你又不知道,因此假设这些表达方式无法进一步考虑,业连管将是共同因素和其余因素的产物。

  

  播放段落

  $\begin{align*}LCM = \textcolor{red}{2} \cdot 2 \cdot 3 \cdot a \cdot \textcolor{red}{b} \cdot b\end{align*}$
  ::LCM=223abb

  播放段落

  Answer : The least common multiple of  $\begin{align*}4ab^2\end{align*}$   and $\begin{align*}6b\end{align*}$   is  $\begin{align*}12ab^2.\end{align*}$
  ::答复:4ab2和6b中最不常见的乘数为12ab2。

  播放段落

  b. To find the LCM of  $\begin{align*}x^2 + 5x - 14\end{align*}$   and  $\begin{align*}2x-4,\end{align*}$  begin by factoring each expression.
  ::b. 找到x2+5x-14和2x-4的 LCM,首先考虑每个表达式。

  播放段落

    •   $\begin{align*}x^2 + 5x - 14 = (x+7)\color{red}{(x-2)}\end{align*}$
  ::• x2+5x-14=(x+7)(x-2)

  播放段落

    •   $\begin{align*}2x-4=2\color{red}{(x-2)}\end{align*}$
  ::• 2x-4=2x-2

  播放段落

  The  LCM will be the product of the common factors and remaining factors, but this time, the factors include binomials.
  ::业连管将是共同因素和剩余因素的产物,但这一次的因素包括二元论。

  播放段落
  • $\begin{align*}LCM=2\textcolor{red}{(x-2)}(x+7)\end{align*}$
    
    ::LCM=2(x-2)(x+7)

  播放段落

  Answer: The least common multiple of $\begin{align*}x^2 + 5x - 14\end{align*}$   and $\begin{align*}2x-4\end{align*}$   is  $\begin{align*}2(x-2)(x+7).\end{align*}$
  ::答复:x2+5x-14和2x-4的最小公倍数为2(x-2)(x+7)。

  播放段落

  This same logic is applied to find the least common denominator of two or more fractions.
  ::使用同样的逻辑来找到两个或两个以上分数的最小共同分母。

   

   

  ---

  播放段落

  Activity 2: Adding Rational Expressions
  ::活动2: 添加理性表达式

  播放段落

  Now that you know how to find the LCD of a rational fraction, you can  write the harmonic mean  $\begin{align*}\frac{2}{\frac{1}{a}+\frac{1}{b}}\end{align*}$  in a simpler form. B egin by adding the fractions in the denominator. To add these fractions, multiply each denominator by a value which will result in the least common denominator. The LCD of a and b is  $\begin{align*}ab.\end{align*}$  To turn  $\begin{align*}a\end{align*}$  into  $\begin{align*}ab,\end{align*}$  multiply it by  $\begin{align*}b.\end{align*}$   However, as you saw above, you cannot multiply the denominator of a fraction by a value without multiplying the numerator by the same value. M ultiplying both the numerator and the denominator by the same value will produce an equivalent fraction.
  ::如果您知道如何找到一个理性分数的液晶体, 您可以以更简单的形式写出正弦值 21a+1b。 开始在分母中添加分数。 要添加这些分母, 将每个分母乘以导致最小公分母的值。 a 和 b 的液晶体是 ab。 要将 a 变成 ab, 乘以 b。 但是, 如上所示, 在不将分子乘以相同值的情况下, 您无法将一个分母的分母乘以一个值。 乘以数字和分母, 将会产生相等的分数 。

  播放段落
  • $\begin{align*}\frac{1}{a}\cdot\frac{b}{b}=\frac{b}{ab}\end{align*}$  
    ::1abb=巴巴
  播放段落
  • $\begin{align*}\frac{1}{b}\cdot\frac{a}{a}=\frac{a}{ab}\end{align*}$  
    ::1个baa=aaab

  播放段落

  Substitute these into the original formula and add. To add fractions with a common denominator, add the numerators and keep the common denominator.
  ::将其替换为原始公式并添加。要添加具有共同分母的分数,请添加分子并保留共同分母。

  播放段落

  $$\begin{align*}\frac{2}{\frac{b}{ab}+\frac{a}{ab}} = \frac{2}{\frac{b\:+\:a}{ab}}\end{align*}$$
  ::2bab+aab=2b+aab

  播放段落

  As far as adding fractions goes, you are finished. However,  the expression could be  simplified further by dividing the  numerator 2 by the denominator  $\begin{align*}\frac{b+a}{ab}.\end{align*}$
  ::就添加分数而言,您已经完成了。 但是, 表达式可以通过将分子2除以b+aab的分母来进一步简化 。

  播放段落

  $$\begin{align*}\frac{2}{\frac{b\:+\:a}{ab}}=2\div\frac{b\:+\:a}{ab}=2\cdot\frac{ab}{b+a}=\frac{2ab}{b+a}\end{align*}$$
  ::2 b+aaab=2 b+aaaab=2abb+a2abb+a

  播放段落

  T he commutative property can be used to write the  $\begin{align*}b+a\end{align*}$  in the final answer as $\begin{align*}a+b.\end{align*}$
  ::在最后答复中,可使用通量财产将b+a写成a+b。

  播放段落

  Answer:   $\begin{align*}\text{Harmonic Mean}=\frac{2ab}{a+b}\end{align*}$
  ::答复:调温平均=2aba+b

  播放段落

  Although these problems may look difficult, you are just adding fractions. The steps for adding rational expressions  are a generalized version of the steps needed to add fractions.
  ::尽管这些问题看起来可能很困难,但你只是在添加分数。 添加合理表达的步骤是增加分数所需的步骤的通用版本。

  播放段落
  1. Factor the numerators and find the least common denominator.
     ::乘以点数并找到最小的共同分母。
  播放段落
  2. Multiply each fraction to produce equivalent fractions, each with the least common denominator.
     ::乘以每一分数产生等效分数,每个分数的公分母最小。
  播放段落
  3. Add the numerators and keep the denominator.
     ::添加分子并保留分母。
  播放段落
  4. Simplify if possible.
     ::尽可能简化。

  播放段落

  A pply these same strategies to a more complicated problem.
  ::对更复杂的问题采用同样的战略。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Add:  $\begin{align*}\frac{x+5}{x^2-3x} + \frac{3}{x^2+2x}\end{align*}$ .
  ::加:x+5x2-3x+3x2+2x。

  播放段落

  First factor each denominator to find the LCD. The first denominator is $\begin{align*}x^2-3x=x(x-3)\end{align*}$ . The second denominator is $\begin{align*}x^2+2x=x(x+2).\end{align*}$  Both denominators have a single  $\begin{align*}x\end{align*}$ , so you  only need to list it once. The LCD is $\begin{align*}x(x-3)(x+2)\end{align*}$ .
  ::找到液晶体体的第一个分母为 x2 - 3x=x(x- 3) 。 第一个分母为 x2 - 3x=x(x- 3) 。 第二个分母为 x2+2x=x(x+2) 。 两个分母都有一个单一 x, 所以只需列出一次。 液晶体为 x( x-3)(x+2) 。

  播放段落

  $$\begin{align*}\frac{x+5}{x^2-3x} + \frac{3}{x^2+2x} = \frac{x+5}{x(x-3)} + \frac{3}{x(x+2)}\end{align*}$$
  ::x+5x2 - 3x+3x2+2x=x+5x(x-3)+3x(x+2)

  播放段落

  Looking at the two denominators factored, you  can see that the first fraction needs to be multiplied by $\begin{align*}\frac{x+2}{x+2}\end{align*}$ and the second fraction needs to be multiplied by $\begin{align*}\frac{x+3}{x+3}\end{align*}$ .
  ::查看两个分母系数后,可以看到第一个分母需要乘以 x+2x+2,第二个分母需要乘以 x+3x+3。

  播放段落

  $$\begin{align*}&= {\color{red}\frac{x+2}{x+2}} \cdot \frac{x+5}{x{\color{blue}(x-3)}} + \frac{3}{x{\color{red}(x+2)}} \cdot {\color{blue}\frac{x-3}{x-3}} \\\\ &= \frac{(x+2)(x+5)+3(x-3)}{x{\color{red}(x+2)} {\color{blue}(x-3)}}\end{align*}$$
  ::=x+2x+2x+2xx+5x(x-3)+3x(x+2)xx-3x-3x=(x+2)(x+5)+3(x-3)xx(x+2)xx(x+2)x(x+2)(x-3)x(x+2)(x-3)

  播放段落

  At this point, FOIL the first expression in the numerator and distribute the 3 to the second. Lastly, combine like terms .
  ::此时,FOIL是分子中的第一个表达式,然后将三号分布到第二号。最后,将类似术语合并在一起。

  播放段落

  $$\begin{align*}&= \frac{x^2+7x+10+3x-9}{x(x+2)(x-3)}\end{align*}$$
  ::=x2+7x+10+3x-9x(x+2)(x-3)

  播放段落

  Answer:  $\begin{align*}\frac{x^2+10x+1}{x(x+2)(x-3)}\end{align*}$  
  ::答复:x2+10x+1x(x+2)(x-3)

  播放段落

  You  should always check to see if t he rational expression is factorable. In this case, the expression in the numerator is not factorable .
  ::您应该总是检查一下是否合理表达式是因数。 在此情况下, 分子中的表达式是不可因数的 。

   

   

   

  ---

  播放段落

  Activity 3: Subtracting Rational Expressions
  ::活动3:减法合理表达式

  播放段落

  The process for subtracting rational expressions is the same as adding rational expressions with the exception that you are subtracting instead of adding. Be careful when subtracting the numerators. Subtracting an expression will require the to ensure that each term in the expression is subtracted.
  ::减去理性表达式的过程与添加理性表达式的过程相同,但您要减去而不是添加。在减去数字时要小心。减法将需要一个表达式需要确保将表达式中的每个词都减去。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Subtract  $\begin{align*}\frac{x-1}{x^2+5x+4} - \frac{x+2}{2x^2+13x+20}\end{align*}$ .
  ::减号 x-1x2+5x+4-x+22x2+13x+20。

  播放段落

  To find the LCD, first factor the denominators.
  ::要找到液晶,首先考虑分母。

  播放段落

  $$\begin{align*}x^2+5x+4 &= {\color{red}(x+1)} {\color{green}(x+4)} \\ 2x^2+13x+20 &= {\color{blue}(2x+5)} {\color{green}(x+4)} \\ LCD &= {\color{red}(x+1)} {\color{blue}(2x+5)} {\color{green}(x+4)}\end{align*}$$
  ::x2+5x+4=(x+1)(x+4)(x+4)2x2+13x+20=(2x+5)(x+4)LCD=(x+1)(2x+5)(x+4)

  播放段落

  Now  multiply both of the fractions in the subtraction problem by a new fraction, equivalent to 1, which will result in a new fraction with the LCD in the denominator. C ombine the two fractions and simplify.
  ::现在将减法问题的两个分数乘以一个新的分数, 相当于 1, 这将产生一个与分母中的液晶值相加的新分数。 合并两个分数并简化 。

  播放段落

  $$\begin{align*}\frac{x-1}{x^2+5x+4} - \frac{x+2}{2x^2+13x+20} &= \frac{x-1}{{\color{red}(x+1)} {\color{green}(x+4)}} - \frac{x+2}{{\color{blue}(2x+5)}{\color{green}(x+4)}} \\\\ &= {\color{blue}\frac{2x+5}{2x+5}} \cdot \frac{x-1}{{\color{red}(x+1)}{\color{green}(x+4)}} - \frac{x+2}{{\color{blue}(2x+5)}{\color{green}(x+4)}} \cdot {\color{red}\frac{x+1}{x+1}} \\\\ &= \frac{(2x+5)(x-1)-(x+2)(x+1)}{{\color{red}(x+1)}{\color{blue}(2x+5)}{\color{green}(x+4)}} \\\\ &= \frac{2x^2+3x-5-(x^2+3x+2)}{{\color{red}(x+1)}{\color{blue}(2x+5)}{\color{green}(x+4)}} \\\\ &= \frac{2x^2+3x-5-x^2-3x-2}{{\color{red}(x+1)}{\color{blue}(2x+5)}{\color{green}(x+4)}} \\\\ &= \frac{x^2-7}{(x+1)(2x+5)(x+4)}\end{align*}$$
  ::x - 1x2+5x+4x+4x+4x+4x+4x+2x2x2x2xx+5(x+4)=2x+52x+5x2(2x+4)=2x+52x+5x1x1(x1+1x+4)x+2+2x5(x+4x+4x+4x4x4x4x+4x4x4x+4x+4x2x+2x2x2+2x2x+5)(x1x+5)(2x+4)=2x+52x+5x+5x-2x-2x-3x-2x-3x2(x2x+5)(x2x+5)(x+2x+2x+5)(x+4)x=x2x7(x+1)(2x+5)(2x+5)(x+4)

    $\begin{align*}\ \\\end{align*}$

  播放段落

  Answer:  $\begin{align*}\frac{x^2-7}{(x+1)(2x+5)(x+4)}\end{align*}$  
  ::答复:x2-7(x+1)(2x+5)(x+4)

  播放段落

  This  expression cannot be simplified further.
  ::此表达式无法进一步简化 。

   

  播放段落

  Discussion Question : P olynomials are closed under addition, subtraction, and multiplication . Use that information answer the following questions:
  ::讨论问题:多党制在增加、减法和乘法下封闭。

  播放段落
  1. Are rational expressions closed under addition? Will adding two rational expressions always produce a rational expression? Prove your answer.
     ::理性表达是否被加起来了? 增加两个理性表达是否总能产生理性表达? 证明你的回答。
  播放段落
  2. Are rational expressions closed under subtraction? Will subtracting two rational expressions always produce a rational expression? Prove your answer.
     ::理性表达式是否在减法下关闭 ? 减去两个理性表达式是否总能产生理性表达式? 证明您的回答 。

  Summary

  播放段落 To add or subtract rational expressions: 播放段落 Factor the numerators and find the least common denominator. ::乘以点数并找到最小的共同分母。 播放段落 Multiply each fraction to produce equivalent fractions, each with the least common denominator. ::乘以每一分数产生等效分数,每个分数的公分母最小。 播放段落 Add/Subtract the numerators and keep the denominator. ::添加/减号并保留分母。 播放段落 Simplify if possible. ::尽可能简化。 ::要添加或减去理性表达式:乘以分子并找到最不常见的分母。乘以每个分数来产生等同的分母,每个分母都有最不常见分母。添加/减勾并保留分母。如果可能,简化 。

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题