2.1 角和平行线-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节角和平行线

  折叠 展开

  角和平行线

  

  播放段落

  Is the Earth Flat?
  ::地球是平坦的吗?

  播放段落

  Here is an interesting question: "How can you prove the Earth isn't flat? And what tools would you need to determine this?"
  ::这是一个有趣的问题:“你如何能证明地球不是平坦的?你需要用什么工具来确定这一点?”

  播放段落

  for examples to help answer this question!
  ::举例来帮助回答这个问题!

  播放段落

  Today when you  think of a social network, you might  think of platforms like Facebook, Instagram, and Snapchat. In ancient Greece, a social network meant a gathering to share knowledge and ideas. Between the years of about 700 B.C.E. and 100 B.C.E., some of the greatest mathematicians, scientists and philosophers of their era worked together to expand our understanding of how the world works. One of those mathematicians was Eratosthenes of Cyrene. Eratosthenes traveled to Egypt to learn from some of the most knowledgable engineers of antiquity, the Egyptians. He wanted to share the knowledge that the brilliant engineers in Egypt used to build such breathtaking wonders as the pyramids , the Sphinx and more.
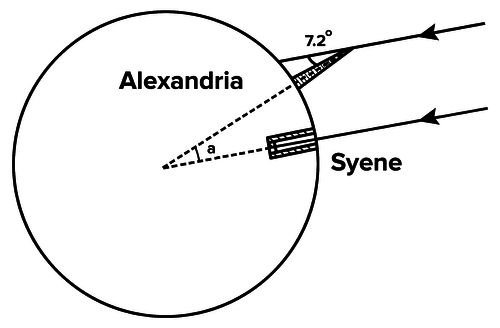
  ::今天,当你想到一个社会网络时,你可能会想到Facebook、Instagram和Snapchat等平台。在古希腊,一个社会网络意味着一个分享知识和思想的聚会。在公元前700年和公元前100年之间,一些他们时代最伟大的数学家、科学家和哲学家一起努力扩大我们对世界运作方式的理解。其中一位数学家是Cyrene的Eratosthenes。Eratosthenes前往埃及学习一些最有知识的古代工程师,即埃及人。他想分享埃及杰出工程师用来构建像金字塔、斯芬克斯等令人惊叹的奇迹的知识。

  

   

  播放段落

  While studying in Egypt, Eratosthenes heard that at noon in the city of Syene on the summer solstice, the sun shown directly into a well and the buildings would cast no shadow because the sun was directly   above them . He also  knew   that, in Alexandria, 800 km (500 mi) north of Syene, if you place a stick in the ground at noon on the same day of the year and  point it   directly upwards, it cast a shadow at a 7.2° angle . Eratosthenes wondered what caused this to happen.
  ::在埃及学习时,埃拉托西内斯听说,夏季宁静时,太阳正午在锡耶内市露出水井,建筑物不会因为太阳直接在水井上方而投下阴影。 他也知道,在塞耶内以北800公里(500米)的亚历山大,如果在同一天中午在地上放置一根棍子并将棍子直接指向上方,它就会在7.2摄氏度的角度投下阴影。 亚拉托西内斯想知道是什么原因导致了这种情况的发生。

  播放段落

  Why was there no shadow in one place,  when there was   a shadow in another place at the same time?
  ::为什么一个地方没有影子,而另一个地方却同时有影子?

  播放段落

  Look at  the image below as you consider your answer.
  ::看着下面的图像,当你考虑你的答案时。

  

  播放段落

  The surface of the Earth is curved. Syene is directly facing the Sun at noon on the summer solstice, and Alexandria is not. Students might say that the Sun hits the surface of the Earth at different angles which is a great observation; however, the Sun is so far that the difference in angle of the rays from the Sun from Alexandria to Syene is 0.00008°. An angle difference this small would not be an easily visible difference to the human eye.
  ::地球表面是弯曲的。 太阳在夏季的休眠中午直接面对太阳, 而亚历山大不是。 学生可能会说太阳从不同角度撞击地球表面,这是一个伟大的观测; 然而,太阳远至太阳从亚历山大到赛恩之间的射线角度差异是0. 008°。 这个小角度的差异对于人类的眼睛来说并不是一个很容易看得见的区别。

  ---

  播放段落

  Angular Thinking
  ::角思维

  播放段落

  To understand how Eratosthenes was able to find the of the Earth , you should review , , and .
  ::为了了解Eratosthenes是如何找到地球的,

  播放段落

  Adjacent Angles are two angles that share a common side. Think of this as two angles that are next to each other.
  ::相邻的角是共同的两个角度。 把它想象成彼此相邻的两个角度 。

  播放段落

  Complementary Angles are two or more angles that add up to 90°.
  ::补充角度是两个或两个以上角度,加起来可达90°。

   

  

  INTERACTIVE

  Complementary Angles

  

  播放段落
  • Move the point to see how the angles add up to ${90}^{\circ }$ .
    ::移动此点以查看角度加起来如何 90 。 @ info: whatsthis
  播放段落
  • The angle measures of the blue and orange angles are displayed below.
    ::蓝色和橙色角的度量如下所示。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  播放段落

  Example
  ::示例示例示例示例

  播放段落
  • What is the complement of a 1 7 ° angle?
    ::17°角的补角是多少?

  播放段落

  $\begin{array}{rl}17+x& =90\\ x& =73\end{array}$
  ::17+x=90x=73

  播放段落
  • What is the complement of an angle with a measure of  $\begin{array}{r}x\end{array}$  degrees?
    ::一个角度与 X 度 的 度量的 补充是什么 ?

  播放段落

  $\begin{array}{r}90-x\end{array}$  degrees
  ::90-x度 90-x度

  播放段落

  Supplementary angles are two or more angles that add up to 180°.
  ::补充角度是两个或两个以上角度,加起来等于180°。

   

  

  INTERACTIVE

  Supplementary Angles

  

  播放段落
  • Move the point to see how the angles add up to 180 degrees.
    ::移动点以查看角度的加起来如何达到 180 度。
  播放段落
  • The angle measures of the blue and orange angles are displayed below.
    ::蓝色和橙色角的度量如下所示。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  播放段落

  Example
  ::示例示例示例示例

  播放段落
  • What is the supplement to a $\begin{array}{r}143\frac{1}{8}\end{array}$  degree angle?
    ::14318度角的补充物是什么?

  播放段落

  $$\begin{array}{rl}143\frac{1}{8}+x& =180\\ x& =36\frac{7}{8}\text{ degrees}\end{array}$$

  
  ::14318+x=180x=36 78度

  播放段落
  • What is the supplement of an angle with a measure of  $\begin{array}{r}x\end{array}$  degrees?
    ::用x度的度量来补充角度是什么?

  播放段落

  $$\begin{array}{r}180-x\text{ degrees}\end{array}$$

  
  ::180-x度

  播放段落

  Vertical angles are opposite angles formed by the intersection of two lines. They are always equal.
  ::垂直角度是两个线条交叉形成的相反角度。 它们总是相等 。

   

  

  INTERACTIVE

  The Angles of Discovery

  

  播放段落

  How are vertical angles, supplementary angles, complementary angles, etc. all connected? 
  ::垂直角度、补充角度、互补角度等如何相互连接?

  播放段落
  • Move the red point $A$  to change the angle measures and see how they all related to each other.
    ::移动红点 A 以改变角度量, 并查看它们之间的关系 。
  播放段落
  • Move the red point  $B$  to rotate all of the angles around the origin they share.
    ::移动红点 B 以在它们共享的源代码周围旋转所有角度 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  播放段落

  Example
  ::示例示例示例示例

  播放段落
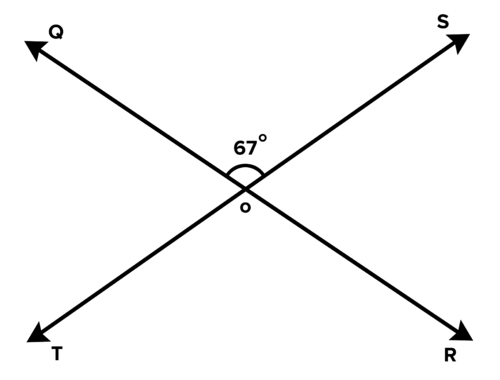
  • Find  $\begin{array}{r}m\mathrm{\angle }QOT\end{array}$ , $\begin{array}{r}m\mathrm{\angle }ROT\end{array}$  , and $\begin{array}{r}m\mathrm{\angle }SOR\end{array}$ . 
    ::找到MOT,MOT,和MSOR。

  

  播放段落

  
  $\begin{array}{r}m\mathrm{\angle }ROT\end{array}$  = 67° because  $\begin{array}{r}\mathrm{\angle }ROT\end{array}$   and  $\begin{array}{r}\mathrm{\angle }QOS\end{array}$   are vertical angles.
  ::mROT = 67 °,因为 @ROT 和 °OS 是垂直角度 。

  播放段落

  $\begin{array}{r}m\mathrm{\angle }QOT\end{array}$  = 113° because  $\begin{array}{r}\mathrm{\angle }QOT\end{array}$  and $\begin{array}{r}\mathrm{\angle }ROT\end{array}$  are supplementary angles.
  ::mOT = 113°,因为 @OT 和 ROT 是补充角度。

  播放段落

  $\begin{array}{r}m\mathrm{\angle }SOR\end{array}$  = 113° because  $\begin{array}{r}\mathrm{\angle }SOR\end{array}$  and $\begin{array}{r}\mathrm{\angle }QOT\end{array}$  are vertical angles.
  ::mSOR = 113°, 因为 QSOR 和 QOT 是垂直角度 。

  播放段落
  • If  $\begin{array}{r}\mathrm{\angle }A\end{array}$  has a measure of  $\begin{array}{r}x\end{array}$  degrees and is vertical to  $\begin{array}{r}\mathrm{\angle }B\end{array}$  what is the measure of   $\begin{array}{r}\mathrm{\angle }B?\end{array}$
    
    ::如果 A 有 x 度的量度, 是垂直到 B 的度量, 那么 B 的度量是多少 ?

  播放段落

  $\begin{array}{r}x\end{array}$  degrees, because  $\begin{array}{r}\mathrm{\angle }A\end{array}$  and  $\begin{array}{r}\mathrm{\angle }B\end{array}$  are vertical angles and vertical angles are equal.
  ::x 度, 因为 A 和 B 是垂直角度, 而垂直角度是相等的 。

   

  ---

  播放段落

  Transversals
  ::跨转

  播放段落

  A transversal is a line that passes through two or more lines. The lines intersected by the transversal don’t have to be parallel , but when they are they have certain properties that can be used to solve a wide variety of math problems. Transversals with parallel lines can be used to solve problems that commonly arise in construction, engineering, and a whole host of other situations – they can even be used to find the circumference of the Earth.
  ::横向线是一条穿过两条或更多条线的线条。 由横向线条交叉的线条不一定是平行的,但是当它们具有某些特性,可以用来解决各种各样的数学问题的时候。 具有平行线的横向线可以用来解决建筑、工程和其他一系列情况中通常出现的问题 — — 它们甚至可以用来寻找地球的环绕度。

  播放段落

  Use the interactive below to explore angles formed by a transversal of parallel lines.
  ::使用下面的交互方式来探索由平行线条交叉形成的角度。

   

  

  INTERACTIVE

  Transversals

  

  播放段落
  • Move the red points to change the lines.
    ::移动红点以更改线条 。
  播放段落
  • Which angles are congruent to each other?
    ::哪个角度彼此一致?

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

   

   

   

  ---

  播放段落

  Properties of Angles in Transversals
  ::横切面中角的属性

  播放段落

  The  table below contains a summary of the relationships between angles  created by  a transversal of parallel lines.
  ::下表汇总了平行线横向形成的角之间的关系。

  

  播放段落

  About 100 years before Eratosthenes' observation, Aristotle constructed the first known informal proof that the Earth is spherical. Eratosthenes realized that the only way two different locations could produce drastically different shadows was if the Earth was not flat. If the Earth was indeed spherical, it must have a circumference which Eratosthenes set out to calculate. Eratosthenes assumed that because the Sun is so far away, that the rays that hit the Earth are relatively parallel. When Eratosthenes discovered that the sun shone straight down on Syene but cast a 7.2° shadow on Alexandria, he realized that the relatively parallel rays from the Sun create a transversal as pictured below:
  ::亚里士多德建造了第一个已知的关于地球是球体的非正式证据。 亚里士多德意识到,两个不同地点产生截然不同的阴影的唯一方法就是地球不是平坦的。 如果地球确实是球体的,那么它必须有一个环形,由埃拉托塞内斯来计算。 亚里士多德认为,由于太阳距离太远,撞击地球的射线相对平行。 当埃拉托西恩发现太阳直射Syene,但向亚历山大投下7.2度的阴影时,他意识到相对平行的太阳射线会产生下述反向光:

  

  播放段落

  Using , Eratosthenes was able to determine that the angle from Alexandria to Syene formed from the center of the Earth is 7.2°. The Earth is a sphere , with 360 degrees all the way around.
  ::Eratosthenes能够确定从亚历山大到从地球中心形成的太阳的角是7.2°。地球是一个球体,环绕360度。

  播放段落

  T he distance between Alexandria and Syene is now a matter of some debate, but multiple sources place it at 5,000 'Stadia' (an ancient unit of length measure), and convert that to approximately 800 km (500 mi) .
  ::亚历山德里亚与锡耶内之间的距离现在有些争议, 但多个来源将其定位为5000“Stadia”(一个古代长度单位),

  播放段落

  Since Alexandria to Syene represented 7.2° out of the 360°  of the Earth, and they were 800 km apart, that meant  800 km  was equal to   $\begin{array}{r}\frac{7.2}{360}\end{array}$  of the entire circumference of the Earth. Eratosthenes used the following proportion to find the Earth’s circumference:
  ::由于亚历山大至锡恩代表地球360度的7.2°,相距800公里,这意味着800公里相当于地球整个环绕的7.2360公里。

  播放段落

  $$\begin{array}{r}\frac{7.2}{360}=\frac{800}{x}\end{array}$$

  
  ::7.360=800x

  播放段落

  This proportion gives a circumference of 40,000 km (24,855 mi). To get a sense of how close Eratosthenes was (according to the estimated distance from Alexandra and Syene), the real circumference of the Earth is 40,075 km. Eratosthenes used nothing but his knowledge and a stick to find the circumference of the Earth.
  ::这个比例提供了40,000公里的环绕(24,855米),为了了解埃拉托西恩(根据与亚历山德拉和赛恩的估计距离)有多近,地球的真实环绕面积为40,075公里。埃拉托西恩除了他的知识外,没有利用他的知识和棍子来寻找地球的环绕。

  播放段落

  Use the interactive below to practice identifying the missing values of the transversal for yourself.
  ::使用下面的交互方式来练习如何为您自己辨别横向的缺失值。

   

  

  INTERACTIVE

  Find the Angle!

  

  播放段落
  • Answer what the angle value should be for the marked angle.
    ::回答标记角的角值应该是什么 。
  播放段落
  • Note the two horizontal lines are parallel.
    ::请注意,两条水平线是平行的。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

   

  ---

  播放段落

  Are These Lines Parallel?
  ::这些线是平行线吗?

  播放段落

  Problems involving parallel lines arise routinely in engineering because so much of our society is built around straight lines. One transversal problem which you will explore happens in carpentry. Not only do carpenters use the relationships of angles in a transversal to solve problems, but they can also use the measures of the angles to determine if the lines are parallel. Consider the banister below.
  ::涉及平行线的问题经常在工程中出现,因为我们社会上有很多是围绕直线建造的。一个你将要探索的横向问题发生在木工中。木工不仅利用横向角度的关系解决问题,他们还可以使用角度的测量来确定线是否平行。考虑下面的容器。

  

  播放段落

  All of the poles, known as balusters, are cut to be identical. If the banister is not parallel to the stairs, then the carpenter will not be able to fit all of the balusters. Fortunately, this can be measured after the first baluster is put in. If the alternate interior angles are equal, the banister is parallel to the stairs. This technique is used in many other situations to determine if boards are parallel.
  ::所有的柱子, 被称为 balusters , 都被切成相同。 如果容器与楼梯不平行, 那么木匠将无法容纳所有的容器。 幸运的是, 这可以在第一个桶子放进去后进行测量 。 如果其他的内部角度相等, 则容器与楼梯平行 。 在许多其他情况下, 此技术被用来确定板板是否平行 。

  播放段落

  The banister should be parallel to the stairs, but the balusters should also be parallel to each other. A carpenter can use the properties of angles in transversals to determine if two balusters are parallel to each other. Interior angles on the same side (inside) of the banister (transversal) should add to 180.
  ::容器应该与楼梯平行,但面包刀也应该彼此平行。 木匠可以使用横跨天体角的特性来确定两个面包刀是否平行。 容器(内侧)同一侧(内侧)的内部角度应该增加到180个。

  播放段落

  Use the interactive below to determine if the lines shown are parallel. 
  ::使用下面的交互式线,确定显示的线条是否平行。

   

  

  INTERACTIVE

  Parallel or Not?

  

  播放段落
  • Move the red points to position the transversal.
    ::将红点移到横角位置。
  播放段落
  • Click the angles to see their measurements and determine if the blue lines are parallel.
    ::单击角度查看它们的测量结果,并确定是否平行的蓝线。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  播放段落

  Discussion Question
  ::讨论问题

  播放段落

  What are some other situations where lines must be parallel?
  ::哪些其他情况必须齐头并进?

  播放段落

   Summary
  ::摘要

  播放段落
  • Complementary angles add up to 90°. S upplementary angles add up to 180°.
    ::补充角加到90度,补充角加到180度。
  播放段落
  • Vertical angles are opposite angles formed by the intersection of two lines. They are always congruent.
    ::垂直角度是两条线交点形成的相反角度。 它们总是相似的 。
  播放段落
  • Transversals of parallel lines create special pairs of angles that are always congruent: corresponding angles, alternate interior angles, and alternate exterior angles.
    ::平行线的横向设置了特殊的一对角度,这些角度始终是相同的:相应的角度、不同的内部角度和不同的外部角度。
  播放段落
  • Conversely, if corresponding angles, alternate interior angles, or alternate exterior angles  are congruent, the lines must be parallel.
    ::反之,如果相应的角度、不同的内部角度或不同的外部角度是相同的,则线条必须是平行的。