4.8 产生等量y=mx+b-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 计算等量 y = mx+b

  Collapse Expand

  计算等量 y = mx+b

  播放段落

  Speeding Ticket
  ::超速车票

  播放段落

  As you continue your investigation of how mathematics is used by doctors, nurses and first responders, you will be taking a look at how police officers use linear equations on a daily basis. Police officers use math to recreate the scene of car accidents, to make forensic conclusions, and much more. When it comes to linear equations, police officers often use a predetermined linear relationship to give out citations. This can be seen with speeding tickets: the faster someone is traveling above the speed limit, the more costly the fine will be. In this section, you will learn a special way to write and graph linear equations. The method which you will be exploring is called slope-intercept form . Slope- intercept form is a method of writing linear equations using the and y-intercept .
  ::当你继续调查医生、护士和第一反应者如何使用数学时,你将会看到警察每天如何使用线性方程式。警官们使用数学来重建汽车事故现场,作出法医结论,等等。在线性方程式方面,警官们经常使用预先确定的线性关系来提供引证。这可以用超速罚单来看出:某人越快超速,罚款就越昂贵。在本节中,你将学习一种特殊的写法和线性方程式的图形。你将要探讨的方法称为斜度干扰形式。斜度干扰形式是一种使用“y”和“y”来写线性方程式的方法。

  ---

  播放段落

  Bike Rentals
  ::自行车租金

  播放段落

  The lesson discussed how a proportional relationship could be written as $\begin{align*}y=kx.\end{align*}$  The lesson discussed the difference between a proportional equation and a linear equation is that a linear equation can have a non-zero starting point . Combine this information to figure out a strategy for writing linear equations.
  ::课程讨论了如何将比例关系写成y=kx。 课程讨论了比例方程和线性方程之间的差别, 即线性方程可以有一个非零起点。 合并这一信息, 以找到写线性方程的战略 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Natalie is starting her own bike rental business but is debating on whether or not to charge a flat cost for renting a bike. Below  are her two potential business models .
  ::Natalie正在开始自己的自行车租赁业务,但正在讨论是否为租用自行车收取固定费用。 以下是她的两个潜在商业模式。

  播放段落
  • Without Flat Cost: Natalie will charge $3 per hour.
    ::娜塔莉每小时收费3美元。
  播放段落
  • With Flat Cost: Natalie will charge $5 to rent the bike and then $3 per hour.
    ::以平价费用:娜塔莉将收取5美元租车费,然后每小时3美元。

  播放段落

  Use the interactive below to make a table and graph for these two business plans.
  ::使用以下互动方式绘制这两个业务计划的表格和图表。

  播放段落

  Discussion Questions
  ::讨论问题 讨论问题

  播放段落
  1. The business model with no flat cost charges $3 per hour. What would the equation be as a proportional equation?
     ::商业模式没有固定费用,每小时3美元。 平方程式是多少比例方程式?
  播放段落
  2. What is the difference in the y-values for the two plans?
     ::这两个计划的Y值有什么不同?
  播放段落
  3. If the total cost from the plan with no flat cost can be determined with the equation y=3x, how do you think the total cost from the plan which is $5 more can be determined?
     ::如果能够用y=3x等式确定无固定费用计划的总费用,那么如何确定5美元以上的计划总费用?
  播放段落
  4. What is the slope and y-intercept of the plan with no flat cost?
     ::没有固定成本的计划的斜坡和 Y 截取点是什么?
  播放段落
  5. What is the slope and y-intercept of the plan with a flat cost?
     ::平价的计划的斜坡和Y 截取点是什么?
  播放段落
  6. What do you notice about the equations and their respective slopes?
     ::你注意到什么方程 和它们各自的斜坡吗?
  播放段落
  7. What do you notice about the equations and their respective y-intercepts?
     ::你注意到什么方程 和它们各自的 Y 问题吗?
  播放段落
  8. What rigid motion can be used to explain the difference between the two lines?
     ::可以用什么僵硬动议来解释两条线之间的区别?
  播放段落
  9. What translation occurred to get from one line to the other?
     ::从一条线到另一条线,翻译出什么来?

  ---

  播放段落

  Slope-Intercept Form
  ::斜坡- 截取窗体

  播放段落

  Use the interactive below to derive the general form for linear equations.
  ::使用下面的交互方式得出线性方程式的一般形式。

  ---

  播放段落

  Graphing Equations in Slope-Intercept Form
  ::斜坡- 截取窗体的图形等量

  播放段落

  The general format for the slope-intercept form is :
  ::斜坡界面形式的一般格式是:

  播放段落

  $$\begin{align*}\large{y = mx + b}\end{align*}$$
  ::y=mx+b y=mx+b

  播放段落
  • The variable $\begin{align*}m\end{align*}$  represents the slope.
    ::变量m代表斜坡。
  播放段落
  • The variable $\begin{align*}b \end{align*}$  represents the $\begin{align*}y\text{-}\end{align*}$ coordinate of the $\begin{align*}y\text{-}\end{align*}$ intercept.
    ::变量b 代表 Y 界面的 Y 坐标 。
  播放段落
  • The variables $\begin{align*}x \end{align*}$  and y represent the $\begin{align*}x\text{-}\end{align*}$ coordinates and $\begin{align*}y\text{-}\end{align*}$ coordinates of every possible solution for the linear relationship.
    ::变量 x 和 y 代表线性关系的每一种可能解决方案的 x 坐标和 Y 坐标。

  播放段落

  Looking at a linear equation written in this format gives you immediate information about the relationship.  You instantly know that the $\begin{align*}y\text{-}\end{align*}$ intercept will be located at  $\begin{align*}(0, b).\end{align*}$   You  also know the rise and run of the line.  You can follow the rise and run from the $\begin{align*}y\text{-}\end{align*}$ intercept to find another point to plot along the line. By knowing two points, you possess the minimum amount of information required to graph a linear relationship without drawing a table. In summary, you can use the following two steps:
  ::查看以此格式撰写的线性方程式时, 您可以立即获得关于此关系的信息。 您当即知道 y 界面将位于 0, b 处。 您也可以知道该线条的上升和运行。 您可以跟踪该线条的上升和运行, 从 y 界面中找到沿此线绘制的另外一点。 通过了解两个点, 您拥有绘制线性关系的最小数量的信息, 而无需绘制表格。 总之, 您可以使用以下两个步骤 :

  播放段落
  1. Plot the $\begin{align*}y\text{-}\end{align*}$ intercept.
     ::绘制 Y 界面 。
  播放段落
  2. Use the slope to find another point along the line.
     ::利用斜坡沿线找到另一个点。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Graph the equation  $\begin{align*}y = \frac{1}{3}x + 2.\end{align*}$
  ::绘制公式y=13x+2。

  播放段落
  1. Plot the  $\begin{align*}y\text{-}\end{align*}$ intercept. 
     ::绘制 Y 界面 。

  播放段落

       Since $\begin{align*}b \end{align*}$  is 2 and you know that the y-intercept is at $\begin{align*}(0, b),\end{align*}$  the  $\begin{align*}y\text{-}\end{align*}$ intercept is at (0, 2).
  ::由于 b 是 2 , 你知道y 界面是 0, b , y 界面是 0, 2 。

  

  播放段落
  2.  Use the slope to find another point along the line.
     ::利用斜坡沿线找到另一个点。

  播放段落

  The slope is $\begin{align*}\tfrac{1}{3}\end{align*}$  which means that the rise is 1 and the run is 3, meaning that if you go up 1 and 3 to the right, you will arrive at another point. From here, you need to connect the dots. Remember that the line will continue on both sides because there is an infinite number of solutions.
  ::斜坡是 13 表示 上升为 1 , 运行为 3 , 意思是, 如果您向右上升 1 和 3 , 您将会到达另一个点 。 从这里, 您需要连接点 。 记住, 线会继续在两侧, 因为有无限数量的解决方案 。

  

  播放段落

  Use the following interactive to practice graphing linear equations in slope-intercept form.
  ::使用以下交互式方式练习用斜坡截取形式绘制线性方程图。

  ---

  播放段落

  Speeding Ticket Continued
  ::继续超速车票

  播放段落

  C ontinue your real-world application of a speeding ticket and turn it into an equation which will model the linear relationship.
  ::继续你真实世界的超速罚单应用 把它变成一个公式 来模拟线性关系

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Each state has a different formula for determining the cost of a speeding ticket. In  the example, let’s say that the driver must pay $120 for breaking the law and an additional $10 for every mile over the speed limit. What would this relationship look like written in slope-intercept form and how can you use the equation to graph it?
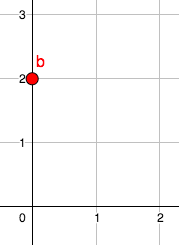
  ::各州在确定超速罚单成本方面都有不同的公式。 比如,我们假设司机必须支付120美元的违法费用以及每英里超速10美元的额外费用。 这种关系会像什么样子写成斜坡拦截形式,以及如何用方程式来绘制?

  播放段落

  Before you write the equation, identify the slope and  $\begin{align*}y\text{-}\end{align*}$ intercept. The y-intercept often represents the starting amount. Since the fine starts at $120, b will be 120, and the  $\begin{align*}y\text{-}\end{align*}$ intercept will be located at (0, 120). The slope is the rate of change . The fine changes by $10 for every mile over the speed limit, so  the slope will be 10. This information gives  you the following equation:
  ::在写方程之前,请标明斜度和 Y 界面。Y 界面通常代表起始量。由于罚款开始为120美元,b 将是120美元,y 界面将位于0,120美元。斜度是变化率。在速度限制上每英里10美元的罚款变化,因此斜度将为10美元。此信息为以下方程:

  播放段落

  $$\begin{align*}y = 10x + 120\end{align*}$$
  ::y=10x+120

  播放段落

  To graph this equation, start at the  $\begin{align*}y\text{-}\end{align*}$ intercept: (0, 120). 
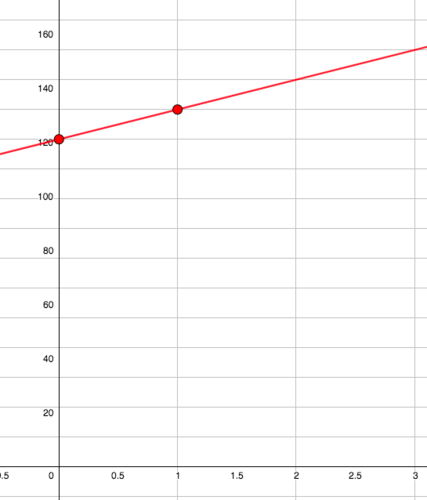
  ::要绘制此方程式, 请从 Y 界面开始 : (0, 120) 。

   

  播放段落

  Next, use the slope of 10 to find another point along the line. The slope of 10 can be written as the improper fraction $\begin{align*}\tfrac{10}{1}\end{align*}$ . The rise is 10 and the run is 1 so if you go up 10 and 1 to the right, you will arrive at another point along the line. By connecting the dots and extending them in both directions, you obtain  the answer. To check this answer choose a random value for $\begin{align*}x,\end{align*}$   substitute it into the equation and check to see if the corresponding $\begin{align*}y\text{-}\end{align*}$ value forms a point that is on the line. If this point is on the line, the answer is likely correct.
  ::下一步, 使用 10 的斜坡沿线找到另一个点 。 10 的斜坡可以写成不合适的部分 101 。 上升为 10 , 运行为 1 。 如果您向右上升为 10 和 1, 则会到达线上的另一个点 。 通过连接点并按双向扩展它们, 您可以获得答案 。 要检查这个答案, 请选择 x 的随机值, 将其替换为方程, 并检查对应的 Y 值是否构成线上的一个点 。 如果这个点在线上, 答案很可能是正确的 。

  

  播放段落

  It appears that $\begin{align*}(2, 140)\end{align*}$   is on the line, how can you check that it is?
  ::似乎(2,140)在电话线上,

  播放段落

  We can check that a point is on the graph mathematically by substituting the values into the equation to see if the equation is true!
  ::我们可以通过将数值替换为方程来检查图形上的点是否正确, 从而从数学角度检查该方程上的一个点是否正确 !

  播放段落

  So, substitute $\begin{align*}(2,140)\end{align*}$   into the equation $\begin{align*}y=10x+120.\end{align*}$
  ::所以,在 y = 10x+120 等式中替换 (2,140) 。

  $$\begin{aligned} (140) &= 10(2)+120\\  140 &= 20+120\\ 140&=140\checkmark\\ \end{aligned}$$

  播放段落

  So, since the equation is true, the point $\begin{align*}(2, 140)\end{align*}$   is on the graph!
  ::所以,既然方程是真实的, 点( 2,140) 在图表上!

  播放段落

     Summary
  ::摘要

  播放段落

  A linear equation in the form  $\begin{align*}y=mx+b\end{align*}$  is a translation of the proportional equation  $\begin{align*}y=mx\end{align*}$ . 
  ::y=mx+b 中的线性方程式是 y=mx 比例方程式的翻译。

  播放段落

  For a linear equation,  $\begin{align*}y=mx+b:\end{align*}$
  ::对于线性方程,y=mx+b:

  播放段落
  • $\begin{align*}m\end{align*}$  is the slope.
    ::m 是斜坡。
  播放段落
  • $\begin{align*}b\end{align*}$  is the y-coordinate of the point where the line crosses the y-axis.
    ::b 是线横越 Y 轴点的 Y 坐标。