课程： 10.5 近似不合理数字-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节近似不合理数字

折叠展开
近似不合理数字
Ancient Square Roots
::古时广场根

Though it may not have occurred to you , as humans developed a stronger understanding of square roots, the structures they built became more and more elaborate. The lesson discussed how shapes can have irrational dimensions. The accuracy with which these dimensions are estimated can have a large impact on the structural integrity of an object. Methods for approximating square roots date all the way back to ancient Babylon. In this section, you will explore some of the methods which have been used by mathematicians is different cultures over time.
::虽然你可能没有想到,随着人类对平方根有了更深刻的了解,他们所建造的结构变得越来越精细。课程讨论了形状如何具有非理性的维度。估计这些维度的准确性可以对物体的结构完整性产生很大影响。接近平方根的方法可以追溯到古代巴比伦。在本节中, 你将探索数学家使用的一些方法, 随着时间的推移是不同的文化。

Method 1 - Guess and Check
::方法1 - 猜测和检查

The first method you will look at does not necessarily have a known origin in history but is based on the definition of a square root. You know that the square root of a number is the number that when squared equals the radicand. Y ou can guess and check values and get closer and closer to the square root. This process can be done using the following steps:
::您要查看的第一种方法不一定具有历史中已知的起源,而是基于平方根的定义。您知道, 一个数字的平方根是平方等于 radicand 的数字。您可以猜测和检查值, 并接近平方根。此进程可以使用以下步骤完成 :

Estimate the square root to the nearest tenth based on how close the radicand is to the smallest perfect square greater than the radicand and the largest perfect square less than the radicand.
::将平方根估计到最接近的十分之十,根据射线线离最最小的完全平方的距离大于射线,而最大的完全正方的距离比射线小。

Check the tenths above or below as needed until you find the value that is closest.
::根据需要检查以上或以下的十分之一,直到找到最接近的值。

Example
::示例示例示例示例

Approximate $\begin{align*}\sqrt{33}\end{align*}$ to the nearest tenth.
::大约33到最近的十分之一。

1. Estimate the square root to the nearest tenth based on how close the radicand is to the smallest perfect square greater than the radicand and the largest perfect square less than the radicand.
::1. 将平方根估计到最近的第十根,根据射线线与最小的完全平方的距离大于射线,最大完全平方的距离小于射线。

The smallest perfect square greater than the radicand is 36 and the largest perfect square less than the radicand is 25. Since 33 is fairly close to 36, estimate that the value is 5.8.
::比半径大半径大最小的完美方块是36,比半径小的最大完美方块是25,因为33接近36,估计值为5.8。

2. Check the tenths above or below as needed until you find the closest.
::2. 根据需要检查上下十分位数,直至找到最接近的位置。

If you square 5.8, you get $\begin{align*}5.8^2=33.64, \end{align*}$ which is greater than 33. If you square 5.7, you get $\begin{align*}3.7^2=32.49,\end{align*}$ which is less than 33. Therefore, $\begin{align*}\sqrt{33} \end{align*}$ must be between 5.7 and 5.8.
::如果5.8平方,得到5.82=33.64,大于33。如果5.7平方,得到3.72=32.49,少于33。因此,33必须在5.7和5.8之间。

33.64 is 0.64 away from 33 and the 32.49 is 0.51 away from 33 , so the closest approximation of $\begin{align*}\sqrt{33}\end{align*}$ to the nearest tenth is 5.7.
::33.64比33差0.64,32.49比33差0.51,因此,最接近33到最接近10是5.7。

Use the interactive below to practice approximating square roots to the nearest tenth using the guess and check method.
::使用下面的交互方法,使用猜测和检查方法,将平方根与最近的十分根大致一致。

Paper Problem
::文件问题

Paper sizes are based on the ratio of width to length. The most common size is A1 which is the standard size of poster paper. The dimensions of A1 paper are 1: $\begin{align*}\sqrt{2}\end{align*}$ in terms of width to length.
::纸张大小以宽度与长度之比为基础。最常见的尺寸是A1,这是海报纸的标准尺寸。A1纸张的尺寸从宽度到长度为1:2。

Example
::示例示例示例示例

If the width of a piece of A1 paper is 23.4 inches, what will the length of the paper be?
::如果A1纸的宽度是23.4英寸,那么纸的长度是多少?

One way to solve for the length to set up a proportion using the ratio:
::使用比例设定比例的长度解答方式之一 :

$\begin{aligned} \frac{1}{\sqrt{2}} = \frac{23.4}{x} \end{aligned}$
$\begin{align*}\frac{1}{\sqrt{2}}=\frac{23.4}{x}\end{align*}$
::12=23.4x

Cross multip lication results in the following:
::交叉乘结果如下:

$\begin{aligned} x = 23.4 \sqrt{2} \end{aligned}$
$\begin{align*}x=23.4\sqrt{2}\end{align*}$
::x=23.42x=23.42

The perfect squares around 2 are 1 and 4. Since 2 is closer to 1, you can estimate $\begin{align*}\sqrt{2}\end{align*}$ to be 1.3. When you check, you see that $\begin{align*}1.3^2 = 1.69\end{align*}$ which is less than 2. See if you can get closer with 1.4: $\begin{align*}1.4^2 = 1.96\end{align*}$ which is still less than 2. However, $\begin{align*}1.5^2 = 2.25\end{align*}$ so the best approximation is 1.4.
::2左右的完美方形是1和4。由于2接近1,您可以估计2是1.3。检查时,您可以看到1.32=1.69,小于2。看看您能否接近1.4:1.4=1.42=1.96,小于2。然而,1.52=2.25, 最佳近似值为1.4。

$\begin{aligned} x = 23.4 \cdot 1.4 \\ x = 32.76 \end{aligned}$
$\begin{align*}&x = 23.4 \cdot 1.4\\ &x = 32.76\end{align*}$
::x=23.41.4x=32.76

The length of the paper will be approximately 32.76 inches.
::文件长度约为32.76英寸。

Method 2 - The Babylonian Approach
::方法2 - 巴比伦方法

Not only did the ancient Babylonians have an understanding of what a square root was, but we know from the tablet YCB7289 that they were also able to approximate square roots of to a high degree of accuracy. The Babylonians used the following algorithm (a series of steps used to solve a math problem):
::古代的巴比伦人不仅了解平方根是什么,而且我们从平板的YCB7289中知道,他们也能够非常准确地估计平方根。巴比伦人使用了以下算法(用来解决数学问题的一系列步骤 ) :

$\begin{aligned} \frac{a + \frac{r}{a}}{2} \end{aligned}$
$\begin{align*}\frac{a + \frac{r}{a}}{2}\end{align*}$
::a+ra2

The variable $\begin{align*}a\end{align*}$ represents the estimation of the solution. The variable $\begin{align*}r\end{align*}$ represents the radicand, the number that you are finding the square root of.
::变量a 表示解决方案的估计值。变量 r 表示弧度,即您正在找到的平方根数。

This algorithm takes the average of the guess, $\begin{align*}a\end{align*}$ , and the ratio of the radicand to the guess.
::这个算法采用猜测的平均值,a, 以及射线与猜测的比率。

Example
::示例示例示例示例

Approximate $\begin{align*}\sqrt{53}\end{align*}$ .
::大约53岁

The perfect squares above and below 53 are 49 and 64. Since 53 is closer to 49 and the square root of 49 is 7, use 7.2 as your guess, $\begin{align*}a. \end{align*}$ The radicand, $\begin{align*}r, \end{align*}$ is 53.
::上方和下方的完美方形是49和64,因为53的方形接近49,49的方根是7,使用7.2来猜测,a。弧线,r,是53。

$\begin{aligned} \frac{7.2 + \frac{53}{7.2}}{2} = \frac{7.2 + 7.36}{2} = \frac{14.56}{2} = 7.28 \end{aligned}$
$\begin{align*}&\frac{7.2 + \frac{53}{7.2}}{2} =\frac{7.2 + 7.36}{2} =\frac{14.56}{2} =7.28\end{align*}$

The real value of $\begin{align*}\sqrt{53}\end{align*}$ is 7.2801098893… Using the Babylonian algorithm and one guess, you were able to find $\begin{align*}\sqrt{53} \end{align*}$ accurately to the hundredths place!
::以巴比伦算法和一种猜想, 你找到了第53个精确到第100个位置!

Why does the Babylonian method work? In theory, if $\begin{align*}a^2 = r, \end{align*}$ then dividing both sides by $\begin{align*}a \end{align*}$ results in $\begin{align*}a = \frac{r}{a}. \end{align*}$ Since $\begin{align*}a \end{align*}$ is just an estimate, $\begin{align*}a^2 \end{align*}$ will not be exactly equal to $\begin{align*}r. \end{align*}$ As a result, i f $\begin{align*}a \end{align*}$ is an underestimate, $\begin{align*}\frac{r}{a} \end{align*}$ will be an overestimate, and vice versa.
::为什么巴比伦方法起作用呢?理论上,如果a2=r,那么将两边除以a=ra的结果。由于a只是估计数,a2将不等于r。结果,如果低估,RA将高估,反之亦然。

Therefore, t he algorithm is approximating the square root by averaging a value below the square root and a value above the square root. The more accurate the initial guess, the more accurate the average will be .
::因此,算法通过平均低于平方根的值和高于平方根的值来接近平方根。最初的猜测越准确,平均值就越准确。

The Babylonians would then redo the process using the resulting average as the new value for $\begin{align*}a. \end{align*}$ This algorithm allowed for incredible precision when approximating .
::然后,巴比伦人将使用由此得出的平均值作为a的新值重做这个过程。这种算法允许在接近时使用令人难以置信的精确度。

Method 3 - The Bakhshali Approach
::方法3 - Bakhshali方法

The Bakhshali Manuscript is the oldest existing document of Indian mathematics and dates back to around 300 CE. This document contains an algorithm used by Indian mathematicians for approximating the square root of a number. The algorithm is an improvement on the algorithm used by the ancient Babylonians . Where the Babylonian algorithm repeatedly found the average between two guesses, this algorithm start s with the average and subtracts the difference from the average to the true value.
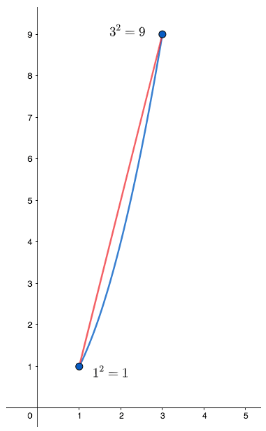
::Bakhshali 手稿是印度现有最古老的数学文档,可追溯到大约300 CE。此文档包含印度数学家用来接近数字平方根的算法。该算法是古代巴比伦人所用算法的改进。巴比伦人算法反复发现两种猜想之间的平均值,此算法从平均值开始,减去平均值与实际值之间的差值。

Using their knowledge of exponential functions, Indian mathematicians realized that the average will always be greater than the true value due to the shape of exponential graphs . This relationship can be seen in the picture below. T he red line represents the average increase between 1 and 3. The blue line represents the square of every number between 1 and 3.
::印度数学家利用他们对指数函数的知识,认识到由于指数图形的形状,平均值总是大于真实值。从下图中可以看到这种关系。红线代表1至3之间的平均增长。蓝线代表1至3之间数字的正方形。

The algorithm on the Bakhshali Manuscript starts with the greatest square root below the radicand. Then , the fractional difference between the value of the radicand and the greatest perfect square below the radicand is added. Lastly, the fractional difference between the number added in the previous step and the true square root is subtracted. The formula appears as follows.
::Bakhshali Manuscript 上的算法以射线下方最大平方根开始。然后添加了射线值与射线下最大完美平方的分数差。最后, 减去了上一步中添加的数字和真实平方根之间的分数差。公式如下。

$\begin{aligned} s + \frac{d}{2 s} - \frac{{(\frac{d}{2 s})}^{2}}{2 (s + \frac{d}{2 s})} \end{aligned}$
$\begin{align*}s + \frac{d}{2s} - \frac{{\left( \frac{d}{2s}\right)}^{2}}{2(s+\frac{d}{2s})}\end{align*}$
::s+d2s-(d2s)22(s+d2s)

$\begin{align*}s \end{align*}$ is the square root of the greatest perfect square less than the radicand
::s 是最完美的平方的平方根比弧度小的平方

$\begin{align*}d \end{align*}$ is the difference between the radicand and the greatest perfect square below the radicand
::d 是射线和射线下最大完美方块的区别

Example
::示例示例示例示例

Approximate $\begin{align*}\sqrt{53}\end{align*}$ .
::大约53岁

The greatest perfect square less than 53 is 49. That means $\begin{align*}s\end{align*}$ will be $\begin{align*}\sqrt{49} = 7 \end{align*}$ and $\begin{align*}d \end{align*}$ will be $\begin{align*}53 - 49 = 4\end{align*}$ .
::最完美的方块小于53是49,这意味着49=7,d为53-49=4。

$\begin{aligned} 7 + \frac{4}{2 (7)} - \frac{{(\frac{4}{2 (7)})}^{2}}{2 (7 + \frac{4}{2 (7)})} & = 7 + \frac{4}{14} - \frac{{(\frac{4}{14})}^{2}}{2 (7 + \frac{4}{14})} \\ = 7 + \frac{2}{7} - \frac{{(\frac{2}{7})}^{2}}{2 (7 + \frac{2}{7})} \\ = 7 + \frac{2}{7} - \frac{\frac{4}{49}}{2 (7 + \frac{2}{7})} \\ = 7 + \frac{2}{7} - \frac{\frac{4}{49}}{2 (\frac{51}{7})} \\ = 7 + \frac{2}{7} - \frac{\frac{4}{49}}{\frac{102}{7}} \\ = 7 + \frac{2}{7} - \frac{4}{49} \cdot \frac{7}{102} \\ = 7 + \frac{2}{7} - \frac{2}{357} \\ = \frac{2499}{357} + \frac{102}{357} - \frac{2}{357} \\ = \frac{2599}{357} \\ = 7.2801120448 \end{aligned}$
$\begin{align*}7 + \frac{4}{2(7)} - \frac{{ \left( \frac{4}{2(7)} \right) }^{2}}{2(7+\frac{4}{2(7)})} &= 7 + \frac{4}{14} - \frac{{ \left( \frac{4}{14} \right) }^{2}}{2(7+\frac{4}{14})} \\ &= 7 + \frac{2}{7} - \frac{{ \left( \frac{2}{7} \right) }^{2}}{2(7+\frac{2}{7})}\\ &= 7 + \frac{2}{7} - \frac{\frac{4}{49}}{2(7+\frac{2}{7})} \\ &= 7 + \frac{2}{7} - \frac{\frac{4}{49}}{2(\frac{51}{7})} \\ &= 7 + \frac{2}{7} - \frac{\frac{4}{49}}{\frac{102}{7}}\\ &= 7 + \frac{2}{7} - \frac{4}{49}\cdot\frac{7}{102} \\ &= 7 + \frac{2}{7} - \frac{2}{357} \\ &= \frac{2499}{357} + \frac{102}{357} - \frac{2}{357} \\ &= \frac{2599}{357} \\ &= 7.2801120448\end{align*}$

The real value of $\begin{align*}\sqrt{53}\end{align*}$ is 7.2801098893... making this estimate accurate to the ten-thousandths place and a huge improvement over the Babylonian method.
::53号的实际价值是72801098893... 使这个估计精确到十万英尺的地方并且比巴比伦法有了巨大的改进

The algorithm used above was a significant accomplishment and helped to set the groundwork for the algorithms used by modern calculators to approximate irrational roots. In fact, m any major mathematical accomplishments have come from Indian mathematicians. The mathematician Aryabhata was the first mathematician to use letters to represent numbers. Brahmagupta introduced 0 to the number system . Srinivasa Ramanujan is famous for his work on infinite series among many other contributions.
::上面使用的算法是一项重大成就,有助于为现代计算器使用的算法打下基础,使其接近非理性根基。事实上,许多主要数学成就都来自印度数学家。数学家阿里亚巴塔(Aryabhata)是第一个使用字母来代表数字的数学家。布拉马古普塔(Brahmagupta)向数字系统引入了0。斯里尼瓦萨·拉马努扬(Srinivasaa Ramanujan)以他关于无限系列的工作和其他许多贡献的出名而闻名。

Summary
::摘要

To use the Guess and Check method for approximating square roots:
::使用 Guess & Check 方法来接近正方根 :

Estimate the square root to the nearest tenth based on how close the radicand is to the smallest perfect square greater than the radicand and the largest perfect square less than the radicand.
::将平方根估计到最接近的十分之十,根据射线线离最最小的完全平方的距离大于射线,而最大的完全正方的距离比射线小。

Check the tenths above or below as needed until you find the value that is closest.
::根据需要检查以上或以下的十分之一,直到找到最接近的值。

章节大纲

常规

近似不合理数字

Ancient Square Roots ::古时广场根

Method 1 - Guess and Check ::方法1 - 猜测和检查

Paper Problem ::文件问题

Method 2 - The Babylonian Approach ::方法2 - 巴比伦方法

Method 3 - The Bakhshali Approach ::方法3 - Bakhshali方法

Summary ::摘要

Ancient Square Roots
::古时广场根

Method 1 - Guess and Check
::方法1 - 猜测和检查

Paper Problem
::文件问题

Method 2 - The Babylonian Approach
::方法2 - 巴比伦方法

Method 3 - The Bakhshali Approach
::方法3 - Bakhshali方法

Summary
::摘要