课程： 10.17圆柱表面积

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节圆柱表面积

折叠展开
圆柱表面积
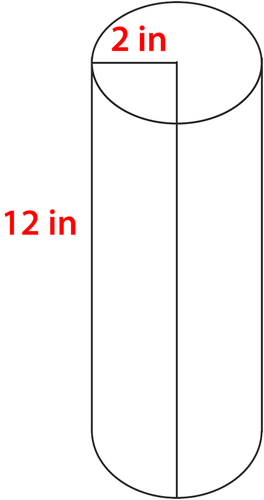
Tevin is in charge of prop design for the Drama Club’s upcoming production. The play will take place in Ancient Rome, so Tevin has to wrap two cylindrical canisters so that they resemble stone pillars. He needs to know the of each canister so he can order the special adhesive covering he needs. Each canister is 12 inches in diameter and 30 inches tall. How can Tevin use this information to figure out the surface area of each canister?
::Tevin负责戏剧俱乐部即将推出的作品的道具设计。剧本将在古罗马进行,因此Tevin必须包扎两个圆柱形圆柱形罐头,以便它们像石柱一样。他需要知道每个罐子的大小,以便他可以订购他所需要的特殊粘合剂。每个罐子直径12英寸,高30英寸。Tevin如何利用这些信息来找出每个罐子的表面面积?

In this concept, you will learn to identify the surface area of cylinders by using .
::在此概念中,您将学会使用来识别气瓶的表面面积。

Finding Surface Area of Cylinders
::圆柱体表面寻找区

A cylinder has two parallel congruent circular bases. The face of the cylinder is one large rectangle .
::一个圆柱体有两个平行的平行相容圆环基。圆柱体的面部是一个大的矩形。

If you were to “unwrap” a cylinder, here is what you would see.
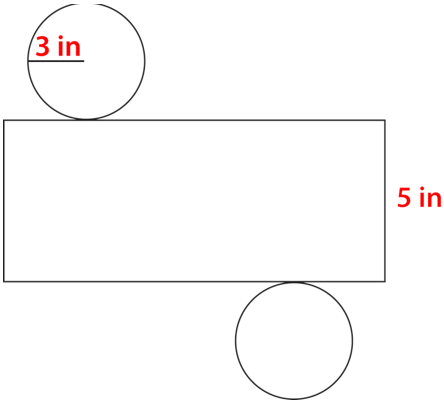
::如果你“打开”一个圆筒,你会看到这个。

This is what the net of a cylinder looks like. To calculate the surface area of a cylinder using a net, you need to figure out the area of the two circles and the area of the rectangle.
::这是圆柱形的网形。要使用网计算圆柱形的表面面积, 您需要找出两个圆圈的面积和矩形的面积。

First, to find the area of a circle , use the following formula.
::首先,要找到圆区域,请使用以下公式。

$\begin{aligned} A = π r^{2} \end{aligned}$

There are two circular bases in the cylinder, so multiply the area of the circle by two for the sum of the two areas.
::圆柱体有两个圆圆基,因此圆圈面积乘以两个圆圆基,这两个圆圆基和圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆的圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆

$\begin{aligned} A = 2 π r^{2} \end{aligned}$

The radius of the circles in the net above is 3 inches. Substitute this given value into the formula and figure out the area of the two circles.
::上方网络圆圈的半径为 3 英寸。将给定值替换为公式, 并找出两个圆圈的面积。

$\begin{aligned} \begin{array}{rcl} A & = & 2 π r^{2} \\ A & = & 2 (3.14) (3^{2}) \\ A & = & 2 (3.14) (9) \\ A & = & 2 (28.26) \\ A & = & 56.52 i n^{2} \end{array} \end{aligned}$

The area of the two circles is 56.52 square inches.
::两个圆圈的面积是56.52平方英寸。

Next, figure out the area of the curved surface. If you look at the net, the curved surface of the cylinder is rectangular in shape.
::下一步, 找出曲线表面的面积。如果您看网, 圆柱形的曲线表面是长方形的。

The length of the rectangle is the same as the of the circle. To find the area of the curved surface, you need to know the circumference (the length) and the height .
::矩形的长度与圆形的长度相同。要找到曲线表面的区域,您需要知道圆周(长度)和高度。

Use this formula to find the area of the rectangle.
::使用此公式查找矩形区域。

$\begin{aligned} \begin{array}{rcl} A & = & 2 π r h \\ A & = & 2 (3.14) (3) (5) \\ A & = & 2 (3.14) (15) \\ A & = & 2 (47.1) \\ A & = & 94.2 i n^{2} \end{array} \end{aligned}$

Then, add the areas.
::然后添加区域。

$\begin{aligned} S A = 56.52 + 94.2 = 150.72 i n^{2} \end{aligned}$

The surface area of the cylinder is $\begin{aligned} 150.72 i n^{2} \end{aligned}$ .
::气瓶表面面积为150.72 i n 2 。

The formula for finding the surface area of a cylinder combines the formula for the area of the top and bottom circles with the formula for finding the area of the rectangular ‘wrap’ around the side. Here is the formula.
::寻找圆柱体表面面积的公式将顶部和底部圆圈面积的公式与寻找侧面矩形“包装”面积的公式结合起来。这是公式。

You can use this formula to find the surface area of the cylinder below.
::您可以使用此公式找到气瓶的表面面积。

First, substitute the given values into the formula.
::首先,将给定值替换为公式。

The radius of the circular bases is 4 cm and the height of the cylinder is 8 cm.
::圆圆基半径为4厘米,圆柱体高度为8厘米。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (4^{2}) + 2 (3.14) (4) (8) \\ S A & = & 2 (3.14) (16) + 2 (3.14) (32) \\ S A & = & 2 (50.24) + 2 (100.48) \\ S A & = & 100.48 + 200.96 \\ S A & = & 301.44 c m^{2} \end{array} \end{aligned}$

The surface area of the cylinder is $\begin{aligned} 301.44 c m^{2} \end{aligned}$ .
::气瓶的表面面积为301.44 cm 2 。

Notice that this works well whether you have a net or a picture of a cylinder. As long as you use the formula and the given values, you can figure out the surface area of the cylinder.
::请注意, 无论您是否有圆柱形的网或图片, 这效果都很好。只要使用公式和给定值, 您可以找到圆柱体的表面区域。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Tevin and the props he’s making for the Drama Club production.
::更早之前, 你曾得知Tevin和他为戏剧俱乐部制作的道具的问题。

Tevin has to create two stone pillars from cylindrical canisters and will be covering their surface area to make them look like stone. Each canister is 12 inches in diameter and 30 inches tall.
::Tevin必须用圆柱形罐制造两块石柱,并覆盖其表面,使其看起来像石头。每根罐子直径12英寸,高30英寸。

First, note the diameter is given instead of the radius, so divide the diameter by 2.
::首先,注意给定直径而不是半径,所以直径除以2。

$\begin{aligned} 12 \div 2 = 6 \end{aligned}$

The radius is 6.
::半径是6

Next, substitute the given values into the formula.
::接下来,将给定值替换为公式。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (6^{2}) + 2 (3.14) (6) (30) \\ S A & = & 2 (3.14) (36) + 2 (3.14) (180) \\ S A & = & 226.08 + 1130.4 \\ S A & = & 1356.48 i n^{2} \end{array} \end{aligned}$

The surface area of each canister is $\begin{aligned} 1356.48 i n^{2} \end{aligned}$ .
::每个罐体的表面面积为1356.48 i n 2 。

Example 2
::例2

Use the formula for finding the surface area of a cylinder to answer the following question.
::使用找到圆柱体表面面积的公式回答下列问题。

What is the surface area of a cylinder with a radius of 6 inches and a height of 12 inches?
::圆柱体半径为6英寸、高度为12英寸的表面面积是多少?

First, substitute the given values into the formula then solve.
::首先, 将给定值替换为公式, 然后解析。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (6^{2}) + 2 (3.14) (6) (12) \\ S A & = & 2 (3.14) (36) + 2 (3.14) (72) \\ S A & = & 226.08 + 452.16 \\ S A & = & 678.24 i n^{2} \end{array} \end{aligned}$

The answer is $\begin{aligned} 678.24 i n^{2} \end{aligned}$ .
::答案是678.24 i n 2。

Example 3
::例3

Find the surface area of the cylinder.
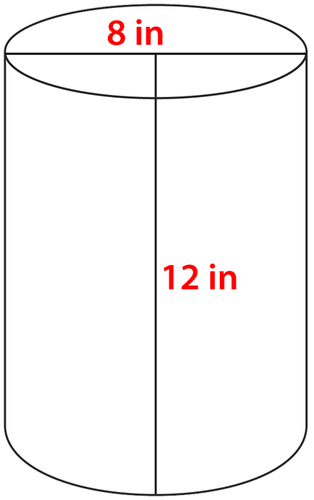
::找到圆柱体的表面区域。

First, substitute the given values into the formula then solve.
::首先, 将给定值替换为公式, 然后解析。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (2^{2}) + 2 (3.14) (2) (12) \\ S A & = & 2 (3.14) (4) + 2 (3.14) (24) \\ S A & = & 25.12 + 150.72 \\ S A & = & 175.84 i n^{2} \end{array} \end{aligned}$

The answer is $\begin{aligned} 175.84 i n^{2} \end{aligned}$ .
::答案是175.84 i n 2 。

Example 4
::例4

Find the surface area of the cylinder.
::找到圆柱体的表面区域。

First, substitute the given values into the formula then solve.
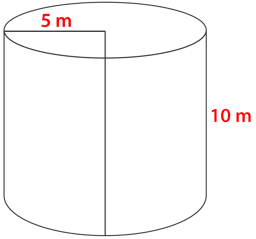
::首先, 将给定值替换为公式, 然后解析。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (5^{2}) + 2 (3.14) (5) (10) \\ S A & = & 2 (3.14) (25) + 2 (3.14) (50) \\ S A & = & 157 + 314 \\ S A & = & 471 m^{2} \end{array} \end{aligned}$

The answer is $\begin{aligned} 471 m^{2} \end{aligned}$ .
::答案是471米2

Example 5
::例5

Find the surface area of the cylinder.
::找到圆柱体的表面区域。

First, note the diameter is given instead of the radius, so divide the diameter by 2.
::首先,注意给定直径而不是半径,所以直径除以2。

$\begin{aligned} 8 \div 2 = 4 \end{aligned}$

The radius is 4.
::半径是4

Next, substitute the given values into the formula then solve.
::下一步,将给定值替换到公式中,然后解析。

$\begin{aligned} \begin{array}{rcl} S A & = & 2 π r^{2} + 2 π r h \\ S A & = & 2 (3.14) (4^{2}) + 2 (3.14) (4) (12) \\ S A & = & 2 (3.14) (16) + 2 (3.14) (48) \\ S A & = & 100.48 + 301.44 \\ S A & = & 402.24 i n^{2} \end{array} \end{aligned}$

The answer is $\begin{aligned} 402.24 i n^{2} \end{aligned}$ .

::答案是402.24 i n 2 。

Review
::回顾

Calculate the surface area of each of the following cylinders using nets. Use the value approximated value 3.14 for the number $\begin{aligned} π . \end{aligned}$
::使用网计算以下每个圆筒的表面面积。使用数值大约为3.14的数值表示。

::[图9]

::[图10]

::[表11]

::[图12]

::[图13]

Calculate the surface area of the following cylinders given these dimensions. Use the value approximated value 3.14 for the number $\begin{aligned} π . \end{aligned}$
::计算以下气瓶的表面面积, 以这些尺寸为准。使用数值大约为 3. 14 的数值, 编号为 + 。

$\begin{aligned} r = 4 i n, h = 8 i n \end{aligned}$
::r = 4 i n, h = 8 i n

$\begin{aligned} r = 5 i n, h = 15 i n \end{aligned}$
::r = 5 i n, h = 15 i n

$\begin{aligned} r = 8 m, h = 16 m \end{aligned}$
::r = 8米,h = 16米

$\begin{aligned} r = 11 m, h = 20 m \end{aligned}$
::r = 11米,h = 20米

$\begin{aligned} r = 3.5 m, h = 8 m \end{aligned}$
::r=3.5米,h=8米

$\begin{aligned} d = 4 f t, h = 6 f t \end{aligned}$
::d = 4 f t, h = 6 f t = 4 f t, h = 6 f t

$\begin{aligned} d = 10 f t, h = 15 f t \end{aligned}$
::d = 10 f t, h = 15 f t = 10 f t, h = 15 f t

$\begin{aligned} d = 20 c m, h = 25 c m \end{aligned}$
::d = 20厘米,h = 25厘米

$\begin{aligned} d = 18 i n, h = 24 i n \end{aligned}$
::d = 18 i n, h = 24 i n

$\begin{aligned} d = 20 f t, h = 45 f t \end{aligned}$
::d = 20 f t, h = 45 f t = 20 f t, h = 45 f t

Review (Answers)
::回顾(答复)

章节大纲

常规

圆柱表面积

Finding Surface Area of Cylinders ::圆柱体表面寻找区

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Finding Surface Area of Cylinders
::圆柱体表面寻找区

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)