计算机科学基础
递归重温
递归解法提供了一种强大的方式来解决自相似问题。接下来我们将探讨二分查找(Binary Search)的解决方案。
二分查找如何工作?
二分查找用于在一个已排序的列表中查找目标项(target)。以下是其工作过程:
- 从第一个基准情况(base case)开始,直接检查中间项是否等于目标项。如果中间项等于目标项,则查找完成并报告其索引。
- 如果列表为空,则报告
-1或“未找到”。 - 如果目标项不等于中间项,判断目标项是大于还是小于中间项,从而决定接下来搜索列表的哪一半。
接下来:
- 如果中间项大于目标项,则在列表的前半部分继续搜索。
- 否则,在列表的后半部分继续搜索。
这与最初的问题相同,表明这是一个递归或自相似的问题。
下图展示了二分查找的代码实现,其中标注了基准情况和递归情况。
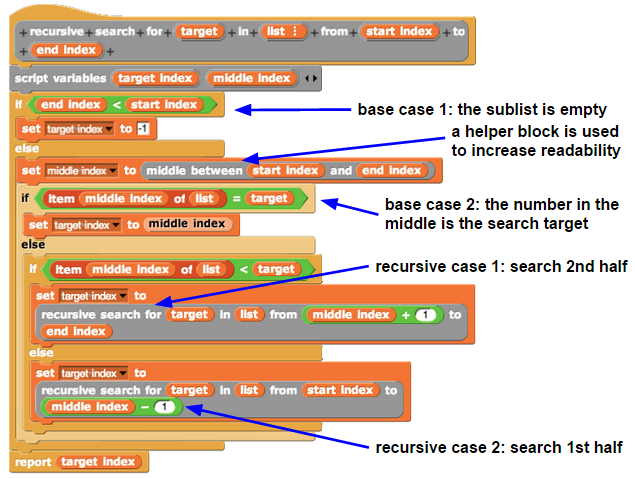
二分查找:抽象简化
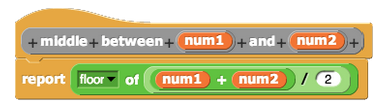
一种简化二分查找解决方案的优秀方法是使用抽象。在前面的代码示例中,使用了一个辅助模块 “middle between”,用于在给定排序列表的首尾索引时计算中间索引(参见下图)。
抽象通过封装功能模块,使得复杂逻辑更加简洁并易于理解,同时保留递归问题的核心逻辑。
另一种简化二分查找解决方案的方法
另一种简化二分查找的方法是通过增加一个抽象层。下图展示了一个辅助模块,其中目标值(target)和列表(list)被作为输入传递给 “binary search for” 模块。实际的递归解决方案在递归搜索模块中实现,该模块根据排序列表的首尾索引执行搜索。通过 “binary search for” 模块,用户可以调用递归搜索,而无需提供首尾索引。用户只需看到启动二分查找所需的基本信息和模块,而看不到递归搜索的具体过程或背后的实现细节。

该二分查找辅助模块通过调用递归搜索模块,在列表中查找目标值,并进一步提升了抽象层次。
二分查找:追踪过程
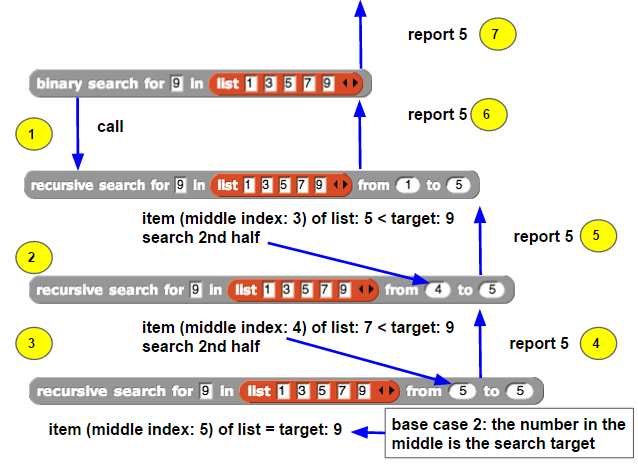
我们之前讨论过如何通过 “binary search for” 模块简化递归搜索的接口,该模块以目标值和列表作为输入(参见下图)。然后调用 “recursive search for” 模块,并立即解决第一个基准情况:目标值 9 不等于中间项 5。由于目标值 9 大于中间项 5(位于中间索引位置),程序开始搜索列表的后半部分(索引 4 到索引 5)。这个过程重复进行,列表被分割并检查位于索引 4 的第一个元素。由于目标值大于 7,递归搜索再次重复,继续搜索列表的后半部分。
基准情况 2 解决了目标值 9 等于列表中的 9,并且位于中间索引 5。
目标值在索引 5 找到后,递归搜索向前返回结果,第二次递归搜索返回给第一次递归搜索。最终,索引 5 被返回给 “binary search for” 模块的顶层,供用户使用。
下图展示了目标值为 9 时,二分查找的追踪过程。通过逐步应用基准情况和递归情况,最终生成报告。
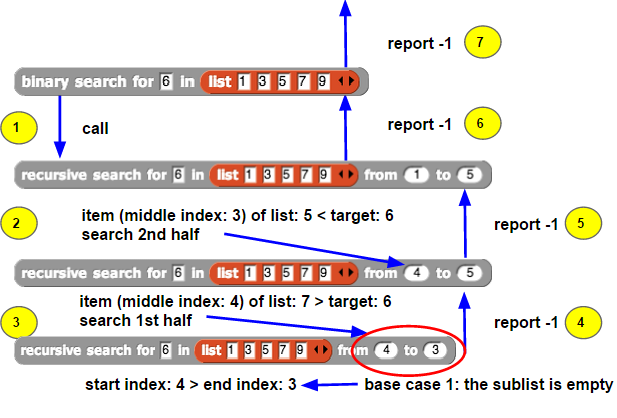
当目标值不在列表中时的情况
如果目标值不在列表中,二分查找会返回 -1(参见下图)。同样的递归搜索调用会执行,但在最后一次调用中,开始索引大于结束索引,这表明目标值不在列表中,且搜索已到达列表末尾。
科赫曲线
1904年,Helge von Koch 发现了科赫雪花曲线,这是一条“在分形几何研究中具有重要意义的连续曲线”。科赫曲线从一条长度为 1 单位的线段开始。随后,该线段被替换为四条新线段,每条长度为原线段的三分之一,这种替换规则被称为生成器。这个过程无限重复,最终形成科赫曲线。下图展示了科赫曲线从第 0 阶到第 2 阶的生成过程。
此图显示了科赫曲线的生成器(第 0 阶)及第 1 阶和第 2 阶的迭代。
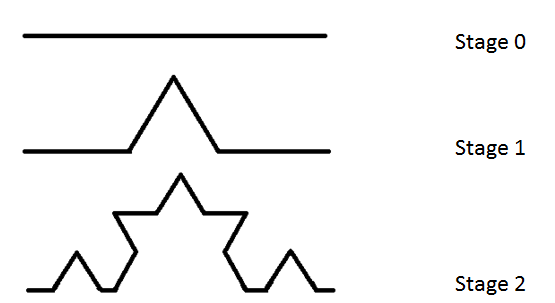
科赫曲线的长度是无限的。该曲线是递归的有趣实现之一,其具有自相似性:曲线不断复制自身。
科赫雪花
将同样的科赫曲线生成器应用于等边三角形的三条边,通过反复迭代,最终形成类似雪花的形状(见科赫雪花)。科赫雪花的周长是无限的,而面积是有限的。
通过观察科赫雪花的每个阶段,可以发现边的段数、每段的长度以及总周长的变化模式如下所示。每条边的段数是前一阶段的四倍。每段的长度每次被等分为三分之一,从而得到新段的长度。由于初始阶段是一个等边三角形,我们将边段数乘以三,再除以段长,并按当前迭代阶段的次数计算总周长。
以下表格展示了科赫雪花在不同迭代阶段的模式。
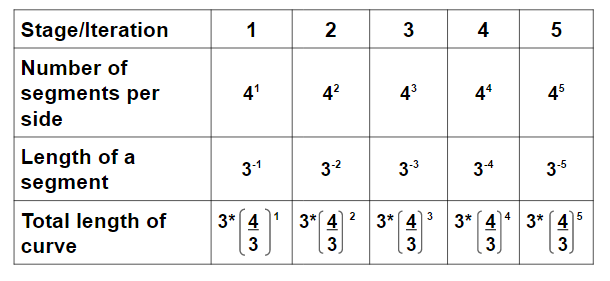
探索问题
通过研究科赫曲线和雪花的模式,可以了解到同一过程的重复如何生成每个阶段。我们可以利用递归过程解决同类问题的抽象。
- 第 N 次迭代的总长度是多少?观察简化前后的数字模式。
- 如果无限次重复该过程,科赫曲线会是什么样子?换句话说,如果无限次迭代,你预计会发生什么?
- 科赫曲线的长度是多少?
- 你能估计每个阶段的面积吗?最终雪花的面积是多少?
通过复习上述问题,我们可以开始观察科赫曲线和科赫雪花的行为模式:
- 根据已建立的模式,第 N 次迭代的总长度为 3⋅(4/3)n3 \cdot (4/3)^n。
- 随着科赫曲线的无限次迭代,曲线将变得更加平滑,线段之间的距离看起来会越来越近,但永远不会相交。
- 科赫曲线的长度是无限的(经过无限次生成器应用后)。
- 最终雪花的面积是有限的(有界的)。