计算机科学基础
计算的限制
我们已经学习了一些计算的重大思想,这些思想通过信息处理让我们能够完成令人惊叹的任务。你可能已经产生了一种印象:如果我们能够量化信息并设计一个算法,就可以通过计算解决任何问题。然而,本章将探讨关于计算限制的理论。计算能力存在理论和实践上的限制。
图灵机再探
当我们讨论“算法”的形式定义时,介绍了图灵机这一计算的数学模型。通过这个模型,我们可以研究计算的本质,包括它可能实现的能力。阿兰·图灵为可计算性理论作出了重要贡献,他的模型机证明了图灵机和我们可以构建的任何计算机一样强大(图灵完备性)。如果我们能够找到一个图灵机无法解决的问题,就证明了这个问题是不可计算的,也就是说,它无法通过任何计算机上的计算来解决。
停机问题
1936年,阿兰·图灵证明了一个通用算法无法解决所有可能的程序-输入对的停机问题,即停机问题是无法通过计算解决的。更具体地说,停机问题是不可判定的,因为这是一个最简单的“是”或“否”决策问题:给定一个程序和一个输入,判断程序是否会最终停止(停机)。显然,通过实际运行程序并查看其是否会停机是不可行的,因为如果程序中有一个无限循环,可能永远不会停止。这个问题的目标是分析程序及其输入,确定程序是否会停机。
图灵通过一种叫做反证法的证明技术证明了停机问题是不可判定的。建议查阅维基百科上的一些反证法示例以加深理解。另一个经典例子是数论中欧几里得定理的证明,该定理断言质数是无限的。所有反证法的证明都以假设我们试图证明的命题是假的开始,经过一系列逻辑有效的步骤,最终得出一个显然错误或矛盾的结论,这表明初始假设是错误的,因为一个命题只能为真或假,不可能同时为真和假。
假设停机问题可判定
如果我们假设停机问题是可判定的/可解决的,那么我们应该能够设计一个算法,并将其实现为一个程序来解决这一问题。该程序应接受一个程序和该程序的输入作为输入参数,并返回答案——即该程序是否会在给定输入上停机。这种程序听起来可能很奇怪,因为它将另一个程序作为输入,但我们已经见过这样的程序,例如,Snap! 中的高阶函数块接受一个代码块(程序)作为输入,一个解释器程序也将程序的源代码作为数据并运行该程序。在计算机科学中,程序本质上是数据,它们之间没有内在的差别。
以下反证证明显示,无法存在一个可以回答停机问题的程序:
反证过程:
-
假设存在一个解
假设有一个程序H能够判定任何程序P和输入I是否会停机。H(P, I)的返回值是:- 如果程序
P在输入I上停机,则返回True; - 如果程序
P在输入I上不会停机,则返回False。
- 如果程序
-
设计一个新程序
D
定义一个新程序D,该程序接受一个程序P作为输入,并调用H自身:- 如果
H(P, P)返回True(即程序P在自身作为输入时会停机),则D进入一个无限循环; - 如果
H(P, P)返回False(即程序P在自身作为输入时不会停机),则D停机。
- 如果
-
矛盾
现在让D自己作为输入运行,即调用D(D):- 如果
H(D, D)返回True,表示程序D停机,则根据D的定义,它会进入无限循环,这是矛盾; - 如果
H(D, D)返回False,表示程序D不停机,则根据D的定义,它应该停机,这也是矛盾。
- 如果
因此,假设 H 存在是错误的,停机问题是不可判定的。
通过这一证明,我们了解了计算的一个基本限制:并非所有问题都能通过算法和计算机解决。这为我们理解计算的理论基础和实际应用设定了界限。
假设存在这样一个程序 A。A(P, D) -> 判断程序 P 在输入数据 D 上是否会停机。
我们可以创建另一个程序 B,它接受一个程序作为输入。在程序 B 的内部,我们可以调用程序 A,并根据输入确定输入程序是否会在自身作为输入数据时停机。如果答案是“否”(不会停机),则程序 B 停机(返回);如果答案是“是”(会停机),则程序 B 进入无限循环。
B(P):
if A(P, P) == "yes":
infinite loop
else:
return
如果我们将程序 B 自身作为输入传递会发生什么?
更简单地说,程序 B 是否会在自身作为输入时停机?这个问题有两种可能的结果:
- 程序 B 在自身作为输入时停机;
- 程序 B 在自身作为输入时永远运行。
实际结果取决于程序 B 内部调用程序 A 的结果。
- 如果程序 B 在自身作为输入时停机,根据程序 B 的设计,它应该进入无限循环(矛盾)。
- 如果程序 B 不会在自身作为输入时停机,那么根据设计,它应该立即返回(矛盾)。
无论哪种情况,结果都是矛盾的。
反证法结论
到目前为止,我们假设了一个前提,遵循了一系列逻辑推理步骤,最终得出了矛盾的结论。
哪里出了问题? 矛盾不可能成立,因为它们在逻辑上是不可能的。
- 推理过程是逻辑正确的;
- 唯一可能错误的地方是我们的假设。
因此,假设不能成立,即停机问题是不可判定的。
视频参考:
难以解决的问题(Intractable Problems)
停机问题是困难的,因为即使在理论上,它也无法通过算法解决。然而,还有一些问题在理论上是可解的,但在实践中几乎不可能解决。我们可以通过已知最佳算法的性能对问题进行分类:
- 简单问题: 如果一个问题可以通过快速算法解决,则计算机可以快速解决它,问题被认为是简单的。
- 困难问题: 如果已知的最佳算法需要很长时间才能解决,则计算机无法快速解决它。
通过算法复杂性理论,我们可以根据算法的复杂性将每个算法归入特定类别。如果一个类别的算法的 Big-O 表示仅包含多项式项,那么可以通过该类别中的算法解决的问题称为 P 问题(存在多项式时间解),例如:
- O(1)O(1)、log2(N)\log_2(N)、O(N)O(N)、O(N2)O(N^2)。
这些 P 问题对计算机来说是“简单”的。
NP 问题
在没有多项式时间解的问题中,有一些问题的解如果被猜测,可以在多项式时间内验证。例如:
- **整数因子分解问题(质因数分解)**没有已知的多项式时间解,但给出答案后,可以通过简单地将因子相乘并比较结果来快速验证。
这些问题被称为 NP 问题(非确定性多项式问题)。
不可解决的问题
对于需要太长时间解决的问题,我们称之为难以解决的问题(Intractable Problems),包括:
- 最优算法时间复杂度为指数级(如 O(2N)O(2^N))的问题;
- 或多项式时间解的指数过大(如 O(N15)O(N^{15}))的问题。
例如,如果一个问题的最佳算法复杂度为 O(2N)O(2^N),并且 N=100N = 100,一台计算机每秒可以执行 101210^{12} 次运算,那么解决这个问题需要大约 4×10104 \times 10^{10} 年(接近宇宙的年龄)。
P 与 NP 的关系
显然,P 是 NP 的子集,因为 NP 问题仅要求答案验证时间为多项式,而能够在多项式时间内解决问题(P)自然符合这个条件。但问题是:
- P 是否等于 NP?
这个问题是计算机科学领域未解决的难题之一。如果你能解决它,你将赢得百万美元的“千禧年大奖问题”。
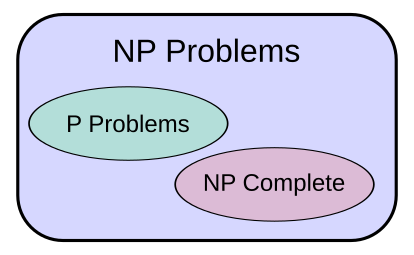
NP 完全问题
为了研究 P vs NP 问题,理论计算机科学家定义了一个新类别:NP 完全问题(NP-complete)。其特点如下:
- 所有 NP 完全问题都有一个共同的性质——所有其他 NP 问题都可以在多项式时间内转换为任何一个 NP 完全问题。
- 如果能解决任何一个 NP 完全问题,就可以证明所有 NP 问题都可在多项式时间内解决,即 P=NPP = NP。
现实意义
- 大多数计算机科学家认为 P≠NPP \neq NP,原因在于:
- 否则,“创造性飞跃”将不复存在,因为解决一个问题和能够识别正确答案一样容易。
- 大多数加密算法的安全性依赖于破解它们是 NP 问题。如果 P=NPP = NP,所有加密技术将被破解。
更多未解决的计算机科学问题,请参考:计算机科学中的未解决问题列表