机器学习
在上一节中,我们看到逻辑模型(如决策树)使用逻辑表达式来划分实例空间。当两个实例最终落在同一个逻辑片段中时,它们是相似的。在本节中,我们将考虑通过实例空间的几何结构来定义相似性的模型。在几何模型中,特征可以描述为二维(x轴和y轴)或三维空间(x、y和z轴)中的点。即使特征本身不是几何的,也可以用几何方式建模(例如,温度随时间的变化可以在两个轴上建模)。在几何模型中,我们可以通过两种方式施加相似性。
- 我们可以使用直线或平面等几何概念来分割(分类)实例空间。这些被称为线性模型。
- 另外,我们可以使用距离的几何概念来表示相似性。在这种情况下,如果两个点彼此靠近,则它们的特征值相似,因此可以归类为相似。我们称这类模型为基于距离的模型。
线性模型
线性模型相对简单。在这种情况下,函数表示为其输入的线性组合。因此,如果 x1 和 x2 是两个标量或相同维度的向量,而 a 和 b 是任意标量,则 表示 x1 和 x2 的线性组合。在最简单的情况下,如果 f(x) 表示一条直线,我们有 形式的方程,其中 c 表示截距, m 表示斜率。
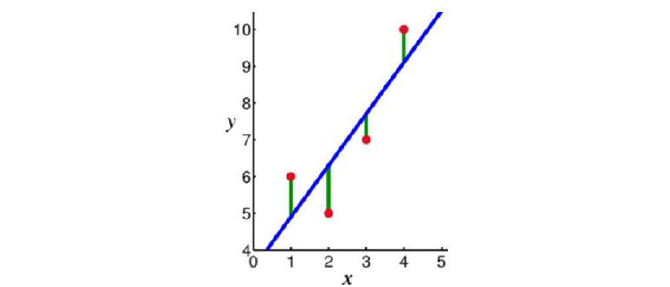
线性模型是参数化的,这意味着它们具有固定的形式,其中包含少量需要从数据中学习的数字参数。例如,在 中,m 和 c 是我们试图从数据中学习的参数。这种技术不同于树模型或规则模型,在这些模型中,模型的结构(例如,在树中使用哪些特征以及在哪里使用)不是预先固定的。
线性模型是稳定的,即训练数据的微小变化对学习到的模型影响有限。相比之下,树模型往往随训练数据变化更大,因为在树的根部选择不同的分裂通常意味着树的其余部分也会不同。由于参数相对较少,线性模型具有低方差和高偏差。这意味着线性模型比其他一些模型更不容易过拟合训练数据。但是,它们更容易欠拟合。例如,如果我们要根据带标签的数据学习国家之间的边界,那么线性模型不太可能给出很好的近似。
基于距离的模型
基于距离的模型是几何模型的第二类。与线性模型一样,基于距离的模型也基于数据的几何结构。顾名思义,基于距离的模型基于距离的概念。在机器学习的背景下,距离的概念不仅仅基于两点之间的物理距离。相反,我们可以考虑两点之间通过运输方式的距离。乘坐飞机在两个城市之间旅行的物理距离比乘坐火车要短,因为飞机不受限制。类似地,在国际象棋中,距离的概念取决于所使用的棋子——例如,主教可以斜向移动。因此,根据实体和移动模式,距离的概念可能会有不同的体验。
常用的距离度量包括欧几里德距离、闵可夫斯基距离、曼哈顿距离和马哈拉诺比斯距离。
距离通过邻居和范例的概念应用。邻居是指通过范例表示的距离度量而言,彼此接近的点。范例可以是根据所选距离度量找到质量中心的质心,也可以是找到最中心数据点的中心点。最常用的质心是算术平均值,它使到所有其他点的平方欧几里德距离最小化。
备注:
- 质心表示平面图形的几何中心,即图形中所有点相对于质心点的算术平均位置。这个定义扩展到n维空间中的任何对象:其质心是所有点的平均位置。
- 中心点在概念上类似于均值或质心。当无法定义均值或质心时,中心点最常用于数据。它们用于质心不能代表数据集的情况,例如在图像数据中。
基于距离模型的例子包括最近邻模型,它们使用训练数据作为范例——例如,在分类中。K-means聚类算法也使用范例来创建相似数据点的聚类。
In the previous section, we have seen that with logical models, such as decision trees, a logical
expression is used to partition the instance space. Two instances are similar when they end up in the
same logical segment. In this section, we consider models that define similarity by considering the
geometry of the instance space. In Geometric models, features could be described as points in two
dimensions (x- and y-axis) or a three-dimensional space (x, y, and z). Even when features are nointrinsically geometric, they could be modelled in a geometric manner (for example, temperature as a
function of time can be modelled in two axes). In geometric models, there are two ways we could
impose similarity.
We could use geometric concepts like lines or planes to segment (classify) the instance space.
These are called Linear models.
Alternatively, we can use the geometric notion of distance to represent similarity. In this case, if
two points are close together, they have similar values for features and thus can be classed as
similar. We call such models as Distance-based models.
Linear models
Linear models are relatively simple. In this case, the function is represented as a linear
combination of its inputs. Thus, if x1 and x 2 are two scalars or vectors of the same dimension
and a and b are arbitrary scalars, then ax1 + bx2 represents a linear combination of x1 and x2. In the
simplest case where f(x) represents a straight line, we have an equation of the form f (x)
= mx + c where c represents the intercept and m represents the slope.
Linear models are parametric, which means that they have a fixed form with a small number of numeric
parameters that need to be learned from data. For example, in f (x) = mx + c, m and c are the
parameters that we are trying to learn from the data. This technique is different from tree or rule
models, where the structure of the model (e.g., which features to use in the tree, and where) is not
fixed in advance.
Linear models are stable, i.e., small variations in the training data have only a limited impact on the
learned model. In contrast, tree models tend to vary more with the training data, as the choice of a
different split at the root of the tree typically means that the rest of the tree is different as well. As a
result of having relatively few parameters, Linear models have low variance and high bias. This implies
that Linear models are less likely to overfit the training data than some other models. However, they
are more likely to underfit. For example, if we want to learn the boundaries between countries based
on labelled data, then linear models are not likely to give a good approximation.
Distance-based models
Distance-based models are the second class of Geometric models. Like Linear models, distance-
based models are based on the geometry of data. As the name implies, distance-based models work on
the concept of distance. In the context of Machine learning, the concept of distance is not based on
merely the physical distance between two points. Instead, we could think of the distance between two
points considering the mode of transport between two points. Travelling between two cities by plane
5
covers less distance physically than by train because a plane is unrestricted. Similarly, in chess, the
concept of distance depends on the piece used – for example, a Bishop can move diagonally. Thus,
depending on the entity and the mode of travel, the concept of distance can be experienced differently.
The distance metrics commonly used are Euclidean, Minkowski, Manhattan, and Mahalanobis.
Distance is applied through the concept of neighbours and exemplars. Neighbours are points in
proximity with respect to the distance measure expressed through exemplars. Exemplars are
either centroids that find a centre of mass according to a chosen distance metric or medoids that find
the most centrally located data point. The most commonly used centroid is the arithmetic mean, which
minimises squared Euclidean distance to all other points.
Notes:
The centroid represents the geometric centre of a plane figure, i.e., the arithmetic mean
position of all the points in the figure from the centroid point. This definition extends to any
object in n-dimensional space: its centroid is the mean position of all the points.
Medoids are similar in concept to means or centroids. Medoids are most commonly used on
data when a mean or centroid cannot be defined. They are used in contexts where the centroid
is not representative of the dataset, such as in image data.
Examples of distance-based models include the nearest-neighbour models, which use the training data
as exemplars – for example, in classification. The K-means clustering algorithm also uses exemplars to
create clusters of similar data points.