机器学习
在玩跳棋游戏时,你会在任何时刻从不同的可能性中选择最佳走法。你思考并运用从经验中获得的学习。这里的学习是,对于一个特定的棋盘,你移动一个棋子,使你的棋盘状态趋向于胜利。现在,同样的学习必须用目标函数来定义。
这里有两种情况需要考虑:直接经验和间接经验。
-
在直接经验中,跳棋学习系统只需要学习如何在大量搜索空间中选择最佳走法。我们需要找到一个目标函数来帮助我们从备选项中选择最佳走法。我们称这个函数为 ChooseMove,并使用符号 来表示这个函数接受来自合法棋盘状态集合 B 的任何棋盘作为输入,并产生来自合法走法集合 M 的某个走法作为输出。
-
当存在间接经验时,学习这样的函数会变得困难。那么,给棋盘状态分配一个实数分数如何?
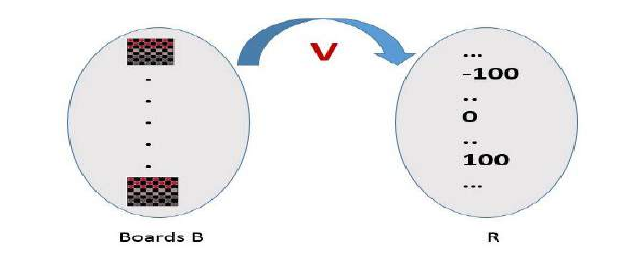
因此,函数为 V:B→R,表示它接受来自合法棋盘状态集合 B 的任何棋盘作为输入,并产生一个实数分数作为输出。这个函数为更好的棋盘状态分配更高的分数。
如果系统能够成功学习这样一个目标函数 V,那么它就可以很容易地利用它从任何棋盘位置选择最佳走法。
因此,我们定义集合 B 中任意棋盘状态 b 的目标值 V(b) 如下:
- 如果 b 是一个获胜的最终棋盘状态,则
- 如果 b 是一个输掉的最终棋盘状态,则
- 如果 b 是一个平局的最终棋盘状态,则
- 如果 b 不是游戏的最终状态,则 ,其中 b′ 是从 b 开始,并以最优方式进行游戏直到结束所能达到的最佳最终棋盘状态。
第 (4) 条是一个递归定义,为了确定特定棋盘状态 V(b) 的值,它需要向前搜索最优的下棋路线,直到游戏结束。因此,我们的跳棋程序无法高效地计算这个定义,我们称之为非操作性定义。
在这种情况下,学习的目标是发现 V 的操作性描述;也就是说,一个可以被跳棋程序在实际时间限制内用于评估状态和选择走法的描述。
通常,完美地学习 V 的这种操作形式可能非常困难。我们期望学习算法只能获得目标函数 V^ 的某种近似。
When you are playing the checkers game, at any moment of time, you make a decision on
choosing the best move from different possibilities. You think and apply the learning that you have
gained from the experience. Here the learning is, for a specific board, you move a checker such that your
board state tends towards the winning situation. Now the same learning has to be defined in terms of
the target function.
Here there are 2 considerations — direct and indirect experience.
During the direct experience, the checkers learning system, it needs only to learn how to choose
the best move among some large search space. We need to find a target function that will help
us choose the best move among alternatives. Let us call this function ChooseMove and use the
notation ChooseMove : B →M to indicate that this function accepts as input any board from the
set of legal board states B and produces as output some move from the set of legal moves M.
When there is an indirect experience, it becomes difficult to learn such function. How about
assigning a real score to the board state.
So the function be V : B →R indicating that this accepts as input any board from the set of legal board
states B and produces an output a real score. This function assigns the higher scores to better board
states.
If the system can successfully learn such a target function V, then it can easily use it to select the best
move from any board position.
Let us therefore define the target value V(b) for an arbitrary board state b in B, as follows:
1. if b is a final board state that is won, then V(b) = 100
2. if b is a final board state that is lost, then V(b) = -100
3. if b is a final board state that is drawn, then V(b) = 0
4. if b is a not a final state in the game, then V (b) = V (b’), where b’ is the best final board state that can
be achieved starting from b and playing optimally until the end of the game.
The (4) is a recursive definition and to determine the value of V(b) for a particular board state, it
performs the search ahead for the optimal line of play, all the way to the end of the game. So this
definition is not efficiently computable by our checkers playing program, we say that it is a
nonoperational definition.
The goal of learning, in this case, is to discover an operational description of V ; that is, a description
that can be used by the checkers-playing program to evaluate states and select moves within realistic
time bounds.
It may be very difficult in general to learn such an operational form of V perfectly. We expect learning
algorithms to acquire only some approximation to the target function ^V.