机器学习
纠错输出码 (ECOC) 方法是一种技术,它允许将多类别分类问题重新构建为多个二元分类问题,从而可以直接使用原生的二元分类模型。
与通过将多类别分类问题划分为固定数量的二元分类问题来提供类似解决方案的一对多 (one-vs-rest) 和一对一 (one-vs-one) 方法不同,纠错输出码技术允许将每个类别编码为任意数量的二元分类问题。当使用**过确定表示(overdetermined representation)**时,它允许额外的模型充当“错误校正”预测,从而带来更好的预测性能。
在纠错输出码 (ECOC) 中,主要的分类任务是根据由基学习器实现的多个子任务来定义的。其思想是,将一个类别与所有其他类别分离的原始任务可能是一个困难的问题。相反,我们希望定义一组更简单的分类问题,每个问题专注于任务的一个方面,通过组合这些更简单的分类器,我们得到最终的分类器。
基学习器是输出为 -1/+1 的二元分类器,并且存在一个 的代码矩阵 W,其中 K 行表示类别,其二进制代码由 L 个基学习器 dj 定义。例如,如果 W 的第二行是 [−1,+1,+1,−1],这意味着要判断一个实例属于 C2 类,该实例应该在 d1 和 d4 的负侧,并且在 d2 和 d3 的正侧。类似地,代码矩阵的列定义了基学习器的任务。例如,如果第三列是 [−1,+1,+1]T,我们理解第三个基学习器 d3 的任务是分离 C1 类的实例与 C2 和 C3 类合并的实例。这就是我们如何形成基学习器的训练集。例如,在这种情况下,所有标记为 C2 和 C3 的实例形成 X3+,标记为 C1 的实例形成 X3−,并且 d3 被训练成使得 输出 +1,而 输出 −1。
代码矩阵因此允许我们用二分类问题 ( 分类问题) 来定义多分类问题 ( 分类问题),并且这是一种适用于使用任何学习算法来实现二分类器基学习器的方法——例如,线性或多层感知器(具有单个输出)、决策树或 SVM,它们的原始定义都是针对两类问题的。
典型的每类一个判别器设置对应于 的对角代码矩阵。例如,对于 :
我们有:
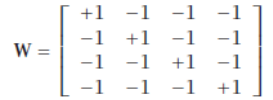
W=1−1−1−1−11−1−1−1−11−1−1−1−11
这里的问题是,如果其中一个基学习器出现错误,可能会导致分类错误,因为类代码词非常相似。因此,纠错码的方法是让 并增加代码词之间的 Hamming 距离。一种可能性是类别的成对分离,其中有一个单独的基学习器来分离 Ci 和 Cj,对于 。在这种情况下,,当 时,代码矩阵为:
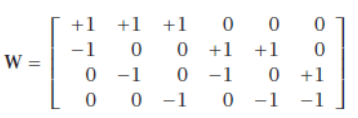
其中 0 表示“不关心”。也就是说,d1 被训练来分离 C1 和 C2,并且不使用属于其他类别的训练实例。类似地,如果 且 ,我们说一个实例属于 C2,并且我们不考虑 d2,d3,d6 的值。这里的问题是 L 是 O(K2),对于大的 K 值,成对分离可能不可行。
如果我们能让 L 很高,我们可以随机生成 的代码矩阵,这样效果会很好,但如果想保持 L 较低,我们需要优化 W。方法是预先设置 L 的值,然后找到 W,使得行之间的距离以及列之间的距离(以 Hamming 距离衡量)尽可能大。对于 K 个类别,有 种可能的列,即二分类问题。这是因为 K 位可以写成 2K 种不同的方式,并且互补(例如,“0101”和“1010”,从我们的角度来看,定义了相同的判别器)将可能的组合除以 2,然后减去 1,因为全 0(或全 1)的列是无用的。例如,当 时,我们有:
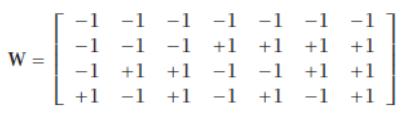
当 K 很大时,对于给定的 L 值,我们从 中选择 L 列。我们希望 W 的这些列尽可能不同,以便基学习器要学习的任务彼此尽可能不同。同时,我们希望 W 的行尽可能不同,以便在一个或多个基学习器失败的情况下,我们能够实现最大的纠错。
ECOC 可以写成一种投票方案,其中 W 的条目 wij 被视为投票权重:
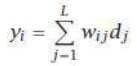
然后我们选择 yi 最高的类别。采用加权和然后选择最大值,而不是检查精确匹配,允许 dj 不再需要是二进制的,而是可以取 −1 到 +1 之间的值,携带软置信度而不是硬决策。请注意,介于 0 和 1 之间的值 pj(例如后验概率)可以简单地转换为介于 −1 和 +1 之间的值 dj,如下所示:
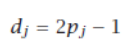
ECOC 的一个问题是,由于代码矩阵 W 是预先设定的,所以不能保证由 W 的列定义的子任务会是简单的。
The Error-Correcting Output Codes method is a technique that allows a multi-class classification
problem to be reframed as multiple binary classification problems, allowing the use of native binary
classification models to be used directly.
Unlike one-vs-rest and one-vs-one methods that offer a similar solution by dividing a multi-class
classification problem into a fixed number of binary classification problems, the error-correcting output
codes technique allows each class to be encoded as an arbitrary number of binary classification
problems. When an overdetermined representation is used, it allows the extra models to act as “error-
correction” predictions that can result in better predictive performance.
In error-correcting output codes (ECOC), the main classification task is defined in terms of a
number of subtasks that are implemented by the base-learners. The idea is that the original task of
separating one class from all other classes may be a difficult problem. Instead, we want to define a set
of simpler classification problems, each specializing in one aspect of the task, and combining these
simpler classifiers, we get the final classifier.
Base-learners are binary classifiers having output −1/ + 1, and there is a code matrix W of K × L whose K
rows are the binary codes of classes in terms of the L base-learners dj. For example, if the second row of
W is [−1,+1,+1,−1], this means that for us to say an instance belongs to C2, the instance should be on the
negative side of d1 and d4, and on the positive side of d2 and d3. Similarly, the columns of the code
matrix defines the task of the base-learners. For example, if the third column is [−1,+1,+1]T , we
understand that the task of the third base-learner, d3, is to separate the instances of C1 from the
instances of C2 and C3 combined. This is how we form the training set of the base-learners. For example
in this case, all instances labeled with C2 and C3 form X+3 and instances labeled with C1 form X− 3 , and d3 is
trained so that xt ∈ X+3 give output +1 and xt ∈ X− 3 give output −1.
The code matrix thus allows us to define a polychotomy (K > 2 classification problem) in terms of
dichotomies (K = 2 classification problem), and it is a method that is applicable using any learninalgorithm to implement the dichotomizer base-learners—for example, linear or multilayer perceptrons
(with a single output), decision trees, or SVMs whose original definition is for two-class problems.
The typical one discriminant per class setting corresponds to the diagonal code matrix where L = K. For
example, for K = 4,
we have
The problem here is that if there is an error with one of the baselearners, there may be a
misclassification because the class code words are so similar. So the approach in error-correcting codes
is to have L > K and increase the Hamming distance between the code words. One possibility is pairwise
separation of classes where there is a separate baselearner to separate Ci from Cj, for i < j. In this case, L
= K(K − 1)/2 and with K = 4, the code matrix is
where a 0 entry denotes “don’t care.” That is, d1 is trained to separate C1 from C2 and does not use the
training instances belonging to the other classes. Similarly, we say that an instance belongs to C 2 if d1 =
−1 and d4 = d5 = +1, and we do not consider the values of d2, d3, and d6. The problem here is that L is
O(K2), and for large K pairwise separation may not be feasible.
If we can have L high, we can just randomly generate the code matrix with −1/ + 1 and this will work
fine, but if we want to keep L low, we need to optimize W. The approach is to set L beforehand and
then find W such that the distances between rows, and at the same time the distances between
columns, are as large as possible, in terms of Hamming distance. With K classes, there are 2(K-1) − 1
possible columns, namely, two-class problems. This is because K bits can be written in 2K different ways
and complements (e.g., “0101” and “1010,” from our point of view, define the same discriminant)
dividing the possible combinations by 2 and then subtracting 1 because a column of all 0s (or 1s) is
useless. For example, when K = 4, we have
When K is large, for a given value of L, we look for L columns out of the 2(K-1 )−1. We would like these
columns of W to be as different as possible so that the tasks to be learned by the base-learners are as
different from each other as possible. At the same time, we would like the rows of W to be as different
as possible so that we can have maximum error correction in case one or more base-learners fail.
ECOC can be written as a voting scheme where the entries of W, wij , are considered as vote weights:
65
and then we choose the class with the highest yi . Taking a weighted sum and then choosing the
maximum instead of checking for an exact match allows dj to no longer need to be binary but to take a
value between −1 and +1, carrying soft certainties instead of hard decisions. Note that a value pj
between 0 and 1, for example, a posterior probability, can be converted to a value dj between −1 and +1
simply as
One problem with ECOC is that because the code matrix W is set a priori, there is no guarantee that the
subtasks as defined by the columns of W will be simple.