机器学习
自举聚合,通常简称为 Bagging,是一种集成学习方法,它让集成中的每个模型都拥有相同的投票权重。为了增加模型的多样性,Bagging 会使用随机抽取的训练集子集来训练集成中的每个模型。例如,随机森林算法就结合了随机决策树和 Bagging,从而实现了非常高的分类准确率。
组合分类器最简单的方法被称为 Bagging,它是 bootstrap aggregating 的缩写,这是该方法的统计学描述。如果你了解什么是“自举”,这很好理解;但如果你不了解,这个词可能就没什么用。自举样本是从原始数据集中有放回地抽取的样本。这意味着我们可能会多次抽取到某些数据点,而其他数据点则可能完全没有被抽取到。自举样本的大小与原始数据集相同,并且会抽取大量的这类样本:通常是 B 个,其中 B 至少为 50,甚至可能达到数千。“自举”(bootstrap)这个名字在计算机科学中比其他领域更受欢迎,因为它也指代计算机启动时运行的第一个程序——自举加载器(bootstrap loader)。这个词源于一句荒谬的说法“picking yourself up by your bootstraps”(意为“提着鞋带把自己提起来”),这暗示着从无到有地开始。
自举抽样看起来是一件非常奇怪的事情。我们拿了一个完美的数据集,通过从中抽样来“搞乱”它。如果这样做能得到一个更小的数据集,那或许是好事(因为它会更快),但我们最终得到的仍然是相同大小的数据集。更糟糕的是,我们还做了很多次。这似乎只是在浪费计算机时间而没有任何收益。但它的好处在于,我们将获得许多表现略有不同的学习器,这正是集成方法所需要的。另一个好处是,我们可以通过投入计算机资源来估计分类函数的准确性,而无需复杂的分析工作(从技术上讲,Bagging 是一种方差降低算法;当我们讨论偏差和方差时,这一点会更清楚)。在获取了一组自举样本之后,Bagging 方法要求我们简单地为每个数据集拟合一个模型,然后通过所有分类器中多数投票的输出来组合它们。下面是一个 NumPy 实现示例,然后我们将看一个简单的例子。
# 计算自举样本
samplePoints = np.random.randint(0,nPoints,(nPoints,nSamples)) # 从0到nPoints-1之间随机生成整数,形状为(nPoints, nSamples)
classifiers = [] # 存储训练好的分类器
for i in range(nSamples): # 遍历每个自举样本
sample = [] # 当前自举样本的特征数据
sampleTarget = [] # 当前自举样本的目标标签
for j in range(nPoints): # 为当前自举样本填充数据
# 假设这里的 'data' 和 'targets' 分别是您的原始特征和标签数据
# sample.append(data[samplePoints[j,i]]) # 实际代码中可能需要从原始数据中提取特征
sampleTarget.append(targets[samplePoints[j,i]]) # 从原始标签中提取标签
# 训练分类器 (假设 self.tree 是一个可以训练决策树的实例)
classifiers.append(self.tree.make_tree(sample,sampleTarget,features))
这个例子包括使用用于演示决策树的聚会数据,并将树限制为“树桩”(stumps),这样它们可以仅基于一个变量进行分类。
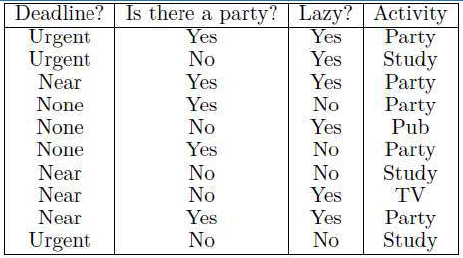
当我们想要构建决策树来决定晚上做什么时,我们首先列出过去几天所做的一切,以获取合适的数据集(这里是过去十天的数据):
使用整个数据集的决策树的输出并不令人惊讶:它会识别出两个最大的类别,并将它们分开。然而,仅使用树桩和 20 个样本,Bagging 就能完美地分离数据,正如这个输出所示:

Bootstrap aggregating, often abbreviated as bagging, involves having each model in the
ensemble vote with equal weight. In order to promote model variance, bagging trains each model in the
ensemble using a randomly drawn subset of the training set. As an example, the random
forest algorithm combines random decision trees with bagging to achieve very high classification
accuracy.
The simplest method of combining classifiers is known as bagging, which stands for bootstrap
aggregating, the statistical description of the method. This is fine if you know what a bootstrap is, but
fairly useless if you don’t. A bootstrap sample is a sample taken from the original dataset with
replacement, so that we may get some data several times and others not at all. The bootstrap sample is
the same size as the original, and lots and lots of these samples are taken: B of them, where B is at least
50, and could even be in the thousands. The name bootstrap is more popular in computer science than
anywhere else, since there is also a bootstrap loader, which is the first program to run when a computer
is turned on. It comes from the nonsensical idea of ‘picking yourself up by your bootstraps,’ which
means lifting yourself up by your shoelaces, and is meant to imply starting from nothing.
Bootstrap sampling seems like a very strange thing to do. We’ve taken a perfectly good dataset,
mucked it up by sampling from it, which might be good if we had made a smaller dataset (since it would
be faster), but we still ended up with a dataset the same size. Worse, we’ve done it lots of times. Surely
this is just a way to burn up computer time without gaining anything. The benefit of it is that we will get
lots of learners that perform slightly differently, which is exactly what we want for an ensemble
method. Another benefit is that estimates of the accuracy of the classification function can be made
without complicated analytic work, by throwing computer resources at the problem (technically,
bagging is a variance reducing algorithm; the meaning of this will become clearer when we talk about
bias and variance). Having taken a set of bootstrap samples, the bagging method simply requires that
we fit a model to each dataset, and then combine them by taking the output to be the majority vote of
all the classifiers. A NumPy implementation is shown next, and then we will look at a simple example.
# Compute bootstrap samples
samplePoints = np.random.randint(0,nPoints,(nPoints,nSamples))
classifiers = []
for i in range(nSamples):
sample = []
sampleTarget = []
for j in range(nPoints):
sampleTarget.append(targets[samplePoints[j,i]])
# Train classifiers
classifiers.append(self.tree.make_tree(sample,sampleTarget,features))
The example consists of taking the party data that was used to demonstrate the decision tree, and
restricting the trees to stumps, so that they can make a classification based on just one variable
When we want to construct the decision tree to decide what to do in the evening, we start by listing
everything that we’ve done for the past few days to get a suitable dataset (here, the last ten days):
The output of a decision tree that uses the whole dataset for this is not surprising: it takes the two
largest classes, and separates them. However, using just stumps of trees and 20 samples, bagging can
separate the data perfectly, as this output shows: