机器学习
让我们用二项式分布的定义(如公式 (1) 所示)来描述 errors(h) 和 errorD(h)。那么我们有:
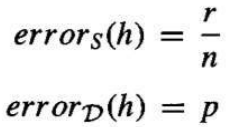
样本误差 errors=r/n
真实误差 errorD=p
其中:
- n 是样本 S 中的实例数量。
- r 是假设 h 错误分类的样本 S 中的实例数量。
- p 是从分布 D 中抽取单个实例被错误分类的概率。
估计量 (Estimator)
errors 是真实误差 errorD
的一个估计量。
估计量是任何用于估计从其中抽取样本的底层总体参数的随机变量。
- 估计偏差 (Estimation Bias):是估计量的期望值与参数真实值之间的差。
定义: 估计量 Y 对任意参数 p 的估计偏差定义为:
Bias(Y)=E[Y]−p
Let us describe errors and errorD
using the terms in Equation (1) defining the Binomial
distribution. We then have
Where,
n is the number of instances in the sample S,
r is the number of instances from S misclassified by h
p is the probability of misclassifying a single instance drawn from D
Estimator:
errors an estimator for the true error errorD
: An estimator is any random variable used to
estimate some parameter of the underlying population from which the sample is drawn
Estimation bias: is the difference between the expected value of the estimator and the true value of
the parameter.
Definition: The estimation bias of an estimator Y for an arbitrary parameter p is