Python 机器学习
线性回归简介
线性回归可以定义为分析因变量与给定自变量集之间线性关系的统计模型。变量之间的线性关系意味着当一个或多个自变量的值发生变化(增加或减少)时,因变量的值也会相应地变化(增加或减少)。
数学上,这种关系可以用以下方程表示:
Y=mX+b
这里:
- Y 是我们要预测的因变量。
- X 是我们用来进行预测的自变量。
- m 是回归线的斜率,表示 X 对 Y 的影响。
- b 是一个常数,称为 Y 截距。如果 ,则 Y 等于 b。
此外,线性关系可以是正向或负向的,解释如下:
正向线性关系 (Positive Linear Relationship)
如果自变量和因变量都增加,则线性关系称为正向。这可以通过以下图表理解:
负向线性关系 (Negative Linear Relationship)
如果自变量增加而因变量减少,则线性关系称为负向。这可以通过以下图表理解:
线性回归的类型
线性回归分为以下两种类型:
- 简单线性回归
- 多元线性回归
简单线性回归 (Simple Linear Regression, SLR)
它是线性回归最基本的版本,使用单个特征预测响应。SLR 的假设是这两个变量之间存在线性关系。
Python 实现
我们可以在 Python 中通过两种方式实现 SLR,一种是提供自己的数据集,另一种是使用 scikit-learn Python 库中的数据集。
示例 1:在以下 Python 实现示例中,我们使用自己的数据集。
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
接下来,定义一个函数,它将计算 SLR 的重要值:
def coef_estimation(x, y):
# 以下脚本行将给出观测值数量 n:
n = np.size(x)
# x 和 y 向量的平均值可以计算如下:
m_x, m_y = np.mean(x), np.mean(y)
# 我们可以找到交叉偏差和关于 x 的偏差,如下所示:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x
# 接下来,回归系数即 b 可以计算如下:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)
接下来,我们需要定义一个函数,它将绘制回归线并预测响应向量:
def plot_regression_line(x, y, b):
# 以下脚本行将绘制实际点作为散点图:
plt.scatter(x, y, color = "m", marker = "o", s = 30)
# 以下脚本行将预测响应向量:
y_pred = b[0] + b[1]*x
# 以下脚本行将绘制回归线并为其添加标签:
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
最后,我们需要定义 main() 函数来提供数据集并调用我们上面定义的函数:
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
# 估计系数
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
# 绘制回归线
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()
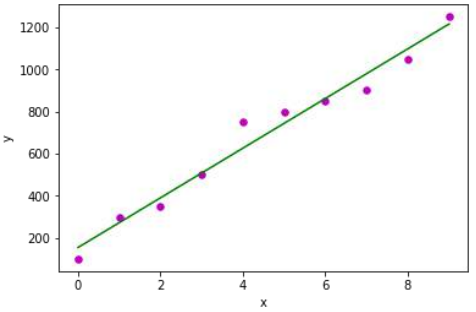
输出:
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788
示例 2:在以下 Python 实现示例中,我们使用 scikit-learn 中的糖尿病数据集。
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
接下来,我们将加载糖尿病数据集并创建其对象:
diabetes = datasets.load_diabetes()
由于我们正在实现 SLR,我们将仅使用一个特征,如下所示:
X = diabetes.data[:, np.newaxis, 2] # 选取第三个特征 (索引为2)
接下来,我们需要将数据分割为训练集和测试集,如下所示:
X_train = X[:-30] # 倒数30个作为测试集
X_test = X[-30:]
接下来,我们需要将目标分割为训练集和测试集,如下所示:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]
现在,要训练模型,我们需要创建线性回归对象,如下所示:
regr = linear_model.LinearRegression()
接下来,使用训练集训练模型,如下所示:
regr.fit(X_train, y_train)
接下来,使用测试集进行预测,如下所示:
y_pred = regr.predict(X_test)
接下来,我们将打印一些系数,如 MSE、方差分数等,如下所示:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))
现在,绘制输出,如下所示:
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
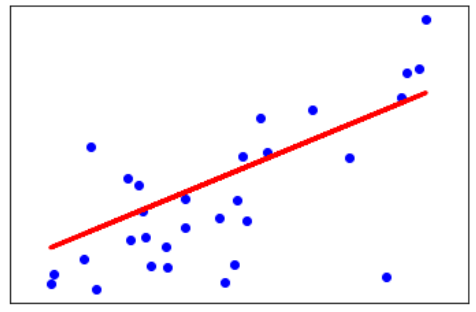
输出:
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
多元线性回归 (Multiple Linear Regression, MLR)
它是简单线性回归的扩展,使用两个或更多特征预测响应。数学上我们可以解释如下:
考虑一个数据集,它有 n 个观测值、p 个特征(即自变量)和 y 作为响应(即因变量),那么 p 个特征的回归线可以计算如下:
![]()
这里,![]() 是预测的响应值,
是预测的响应值,![]() 是回归系数。
是回归系数。
多元线性回归模型总是包含数据中的误差,称为残差误差,这会改变计算,如下所示:
![]() 我们也可以将上述方程写成:
我们也可以将上述方程写成:![]()
Python 实现
在这个例子中,我们将使用 scikit-learn 中的波士顿房价数据集:
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics
接下来,加载数据集,如下所示:
# boston = datasets.load_boston(return_X_y=False) # load_boston 在较新版本的 scikit-learn 中已被移除
# 替代方案:可以使用 fetch_california_housing 或者其他内置数据集,或者从外部加载波士顿数据集
from sklearn.datasets import fetch_california_housing # 以加州房价数据集为例
# 加载加州房价数据集
housing = fetch_california_housing()
X = housing.data
y = housing.target
以下脚本行将定义特征矩阵 X 和响应向量 Y:
# X = boston.data # 如果使用 load_boston
# y = boston.target # 如果使用 load_boston
# 如果使用 fetch_california_housing,X 和 y 已在上面定义
接下来,将数据集分割为训练集和测试集,如下所示:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7,
random_state=1)
现在,创建线性回归对象并训练模型,如下所示:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
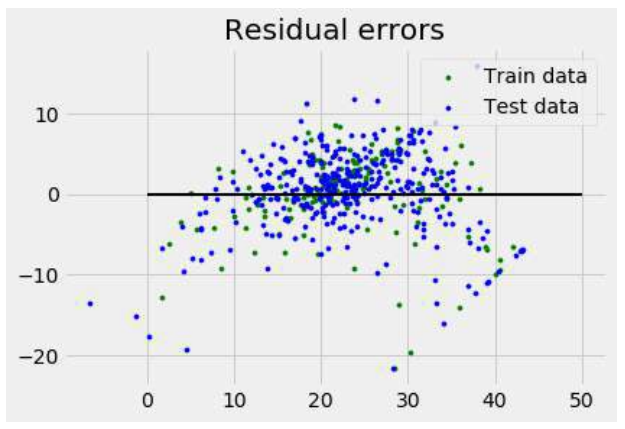
plt.style.use('fivethirtyeight') # 应用图表风格
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = max(reg.predict(X_test).max(), reg.predict(X_train).max()), linewidth = 2) # 修正 xmax 以适应数据范围
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()
输出(请注意,由于使用了不同的数据集,系数和方差分数会不同):
Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
假设 (Assumptions)
线性回归模型对数据集做出了以下一些假设:
- 多重共线性 (Multi-collinearity):线性回归模型假设数据中多重共线性非常少或没有。基本上,当自变量或特征之间存在依赖关系时,就会发生多重共线性。
- 自相关 (Auto-correlation):线性回归模型假设的另一个假设是数据中自相关非常少或没有。基本上,当残差误差之间存在依赖关系时,就会发生自相关。
- 变量之间的关系 (Relationship between variables):线性回归模型假设响应变量和特征变量之间的关系必须是线性的。
16. Regression Algorithms – Linear
Machine Learning Regression
with Python
Introduction to Linear Regression
Linear regression may be defined as the statistical model that analyzes the linear
relationship between a dependent variable with given set of independent variables. Linear
relationship between variables means that when the value of one or more independent
variables will change (increase or decrease), the value of dependent variable will also
change accordingly (increase or decrease).
Mathematically the relationship can be represented with the help of following equation:
Y = mX + b
Here, Y is the dependent variable we are trying to predict
X is the dependent variable we are using to make predictions.
m is the slop of the regression line which represents the effect X has on Y
b is a constant, known as the Y-intercept. If X = 0, Y would be equal to b.
Furthermore, the linear relationship can be positive or negative in nature as explained
below:
Positive Linear Relationship
A linear relationship will be called positive if both independent and dependent variable
increases. It can be understood with the help of following graph:
Positive Linear Relationship
101
Machine Learning with Python
Negative Linear relationship
A linear relationship will be called positive if independent increases and dependent variable
decreases. It can be understood with the help of following graph:
Negative Linear Relationship
Types of Linear Regression
Linear regression is of the following two types:
Simple Linear Regression
Multiple Linear Regression
Simple Linear Regression (SLR)
It is the most basic version of linear regression which predicts a response using a single
feature. The assumption in SLR is that the two variables are linearly related.
Python implementation
We can implement SLR in Python in two ways, one is to provide your own dataset and
other is to use dataset from scikit-learn python library.
Example1: In the following Python implementation example, we are using our own
dataset.
First, we will start with importing necessary packages as follows:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
102
Machine Learning with Python
Next, define a function which will calculate the important values for SLR:
def coef_estimation(x, y):
The following script line will give number of observations n:
n = np.size(x)
The mean of x and y vector can be calculated as follows:
m_x, m_y = np.mean(x), np.mean
We can find cross-deviation and deviation about x as follows:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x
Next, regression coefficients i.e. b can be calculated as follows:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)
Next, we need to define a function which will plot the regression line as well as will predict
the response vector:
def plot_regression_line(x, y, b):
The following script line will plot the actual points as scatter plot:
plt.scatter(x, y, color = "m", marker = "o", s = 30)
The following script line will predict response vector:
y_pred = b[0] + b[1]*x
The following script lines will plot the regression line and will put the labels on them:
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
At last, we need to define main() function for providing dataset and calling the function
we defined above:
103
Machine Learning with Python
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()
Output
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788
Example2: In the following Python implementation example, we are using diabetes
dataset from scikit-learn.
First, we will start with importing necessary packages as follows:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
104
Machine Learning with Python
Next, we will load the diabetes dataset and create its object:
diabetes = datasets.load_diabetes()
As we are implementing SLR, we will be using only one feature as follows:
X = diabetes.data[:, np.newaxis, 2]
Next, we need to split the data into training and testing sets as follows:
X_train = X[:-30]
X_test = X[-30:]
Next, we need to split the target into training and testing sets as follows:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]
Now, to train the model we need to create linear regression object as follows:
regr = linear_model.LinearRegression()
Next, train the model using the training sets as follows:
regr.fit(X_train, y_train)
Next, make predictions using the testing set as follows:
y_pred = regr.predict(X_test)
Next, we will be printing some coefficient like MSE, Variance score etc. as follows:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))
Now, plot the outputs as follows:
plt.scatter(X_test, y_test,
color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
105
Output
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Machine Learning with Python
Multiple Linear Regression (MLR)
It is the extension of simple linear regression that predicts a response using two or more
features. Mathematically we can explain it as follows:
Consider a dataset having n observations, p features i.e. independent variables and y as
one response i.e. dependent variable the regression line for p features can be calculated
as follows:
h(xi ) = b0 + b1xi1 + b2 xi2 + ⋯ + bp xip
Here, h(xi)
is the predicted response value and
b0 , b1 , b2 ... , bp
are the regression
coefficients.
Multiple Linear Regression models always includes the errors in the data known as residual
error which changes the calculation as follows:
h(xi ) = b0 + b1xi1 + b2 x i2 + ⋯ + bp x ip + ei
We can also write the above equation as follows:
yi = h(xi ) + ei or ei = yi − h(xi )
106
Machine Learning with Python
Python Implementation
in this example, we will be using Boston housing dataset from scikit learn:
First, we will start with importing necessary packages as follows:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics
Next, load the dataset as follows:
boston = datasets.load_boston(return_X_y=False)
The following script lines will define feature matrix, X and response vector, Y:
X = boston.data
y = boston.target
Next, split the dataset into training and testing sets as follows:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7,
random_state=1)
Now, create linear regression object and train the model as follows:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
107
Machine Learning with Python
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()
Output
Coefficients:
[-1.16358797e-01
6.44549228e-02
1.65416147e-01
1.45101654e+00
-1.77862563e+01
2.80392779e+00
4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01
9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
Assumptions
The following are some assumptions about dataset that is made by Linear Regression
model:
Multi-collinearity: Linear regression model assumes that there is very little or no multi-
collinearity in the data. Basically, multi-collinearity occurs when the independent variables
or features have dependency in them.
108
Machine Learning with Python
Auto-correlation: Another assumption Linear regression model assumes is that there is
very little or no auto-correlation in the data. Basically, auto-correlation occurs when there
is dependency between residual errors.
Relationship between variables: Linear regression model assumes that the relationship
between response and feature variables must be linear.