Python 机器学习
K-均值算法简介
K-均值聚类算法计算质心并迭代,直到找到最优质心。它假设簇的数量是已知的。它也被称为扁平聚类算法。算法从数据中识别出的簇的数量用 K-均值中的“K”表示。
在此算法中,数据点以这样一种方式分配给簇:数据点与质心之间的平方距离之和最小。需要理解的是,簇内变异性越小,同一簇内的数据点就越相似。
K-均值算法的工作原理
我们可以通过以下步骤理解 K-均值聚类算法的工作原理:
步骤 1:首先,我们需要指定此算法需要生成的簇的数量 K。
步骤 2:接下来,随机选择 K 个数据点,并将每个数据点分配给一个簇。简单来说,根据数据点的数量对数据进行分类。
步骤 3:现在它将计算簇质心。
步骤 4:接下来,重复以下步骤,直到我们找到最优质心,即数据点到簇的分配不再改变:
4.1:首先,计算数据点与质心之间的平方距离之和。
4.2:现在,我们必须将每个数据点分配给比其他簇(质心)更近的簇。
4.3:最后,通过取该簇所有数据点的平均值来计算簇的质心。
K-均值遵循期望最大化方法来解决问题。期望步骤用于将数据点分配到最近的簇,而最大化步骤用于计算每个簇的质心。
在使用 K-均值算法时,我们需要注意以下事项:
- 在使用包括 K-均值在内的聚类算法时,建议对数据进行标准化,因为此类算法使用基于距离的度量来确定数据点之间的相似性。
- 由于 K-均值的迭代性质和质心的随机初始化,K-均值可能会陷入局部最优,并且可能无法收敛到全局最优。这就是为什么建议使用不同的质心初始化。
在 Python 中实现
以下两个实现 K-均值聚类算法的示例将帮助我们更好地理解它:
示例 1
这是一个简单的示例,用于理解 K-均值的工作原理。在此示例中,我们将首先生成包含 4 个不同斑点的 2D 数据集,然后应用 K-均值算法来查看结果。
首先,我们将从导入必要的包开始:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
以下代码将生成包含四个斑点的 2D 数据:
from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60,
random_state=0)
接下来,以下代码将帮助我们可视化数据集:
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
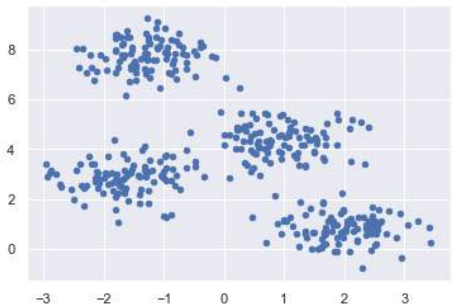
接下来,创建 K-Means 对象并提供簇的数量,训练模型并进行预测,如下所示:
kmeans = KMeans(n_clusters=4, random_state=0, n_init='auto') # 添加 random_state 和 n_init 以确保可复现性和避免警告
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
现在,借助以下代码,我们可以绘制并可视化由 K-均值 Python 估计器选择的簇中心:
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
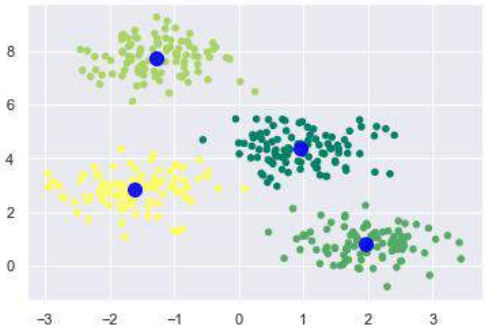
示例 2
让我们看另一个示例,我们将对简单的数字数据集应用 K-均值聚类。K-均值将尝试在不使用原始标签信息的情况下识别相似的数字。
首先,我们将从导入必要的包开始:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
接下来,从 sklearn 加载数字数据集并创建其对象。我们还可以找到此数据集中的行数和列数,如下所示:
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
输出:
(1797, 64)
上述输出显示此数据集包含 1797 个样本和 64 个特征。
我们可以像示例 1 中那样执行聚类:
kmeans = KMeans(n_clusters=10, random_state=0, n_init='auto') # 添加 n_init='auto'
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
输出:
(10, 64)
上述输出显示 K-均值创建了 10 个簇,每个簇有 64 个特征。
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)
plt.show()
输出:
作为输出,我们将获得以下图像,显示 K-均值学习到的簇中心。
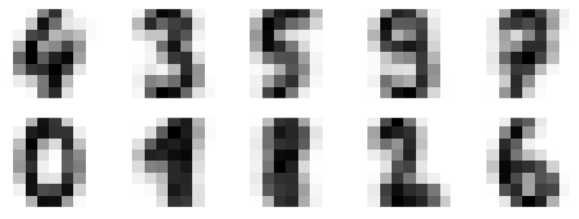
以下代码行将学习到的簇标签与其中找到的真实标签进行匹配:
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0] # 修正 mode 函数的返回值访问方式
接下来,我们可以检查准确率,如下所示:
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)
输出:
0.7935447968836951
上述输出显示准确率约为 80%。
优缺点 (Advantages and Disadvantages)
优点 (Advantages)
以下是 K-均值聚类算法的一些优点:
- 它非常容易理解和实现。
- 如果我们有大量变量,那么 K-均值会比层次聚类更快。
- 在重新计算质心时,实例可以改变簇。
- 与层次聚类相比,K-均值形成的簇更紧密。
缺点 (Disadvantages)
以下是 K-均值聚类算法的一些缺点:
- 预测簇的数量(即 k 的值)有点困难。
- 输出受初始输入(如簇的数量 k 值)的强烈影响。
- 数据的顺序将对最终输出产生强烈影响。
- 它对重缩放非常敏感。如果我们通过归一化或标准化对数据进行重缩放,那么输出将完全改变。
- 如果簇具有复杂的几何形状,则它不擅长聚类工作。
K-均值聚类算法的应用 (Applications of K-Means Clustering Algorithm)
聚类分析的主要目标是:
- 从我们正在处理的数据中获得有意义的直觉。
- 先聚类再预测,其中将为不同的子组构建不同的模型。
为了实现上述目标,K-均值聚类表现得足够好。它可用于以下应用:
- 市场细分
- 文档聚类
- 图像分割
- 图像压缩
- 客户细分
- 分析动态数据中的趋势
18. Clustering Algorithms – K-means
Machine Learning Algorithm
with Python
Introduction to K-Means Algorithm
K-means clustering algorithm computes the centroids and iterates until we it finds optimal
centroid. It assumes that the number of clusters are already known. It is also called flat
clustering algorithm. The number of clusters identified from data by algorithm is
represented by ‘K’ in K-means.
In this algorithm, the data points are assigned to a cluster in such a manner that the sum
of the squared distance between the data points and centroid would be minimum. It is to
be understood that less variation within the clusters will lead to more similar data points
within same cluster.
Working of K-Means Algorithm
We can understand the working of K-Means clustering algorithm with the help of following
steps:
Step1: First, we need to specify the number of clusters, K, need to be generated by this
algorithm.
Step2: Next, randomly select K data points and assign each data point to a cluster. In
simple words, classify the data based on the number of data points.
Step3: Now it will compute the cluster centroids.
Step4: Next, keep iterating the following until we find optimal centroid which is the
assignment of data points to the clusters that are not changing any more:
4.1: First, the sum of squared distance between data points and centroids would
be computed.
4.2: Now, we have to assign each data point to the cluster that is closer than other
cluster (centroid).
4.3: At last compute the centroids for the clusters by taking the average of all
data points of that cluster.
K-means follows Expectation-Maximization approach to solve the problem. The
Expectation-step is used for assigning the data points to the closest cluster and the
Maximization-step is used for computing the centroid of each cluster.
While working with K-means algorithm we need to take care of the following things:
While working with clustering algorithms including K-Means, it is recommended to
standardize the data because such algorithms use distance-based measurement to
determine the similarity between data points.
115
Machine Learning with Python
Due to the iterative nature of K-Means and random initialization of centroids, K-
Means may stick in a local optimum and may not converge to global optimum. That
is why it is recommended to use different initializations of centroids.
Implementation in Python
The following two examples of implementing K-Means clustering algorithm will help us in
its better understanding:
Example1
It is a simple example to understand how k-means works. In this example, we are going
to first generate 2D dataset containing 4 different blobs and after that will apply k-means
algorithm to see the result.
First, we will start by importing the necessary packages:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
The following code will generate the 2D, containing four blobs:
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60,
random_state=0)
Next, the following code will help us to visualize the dataset:
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
116
Machine Learning with Python
Next, make an object of KMeans along with providing number of clusters, train the model
and do the prediction as follows:
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
Now, with the help of following code we can plot and visualize the cluster’s centers picked
by k-means Python estimator:
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
117
Machine Learning with Python
Example 2
Let us move to another example in which we are going to apply K-means clustering on
simple digits dataset. K-means will try to identify similar digits without using the original
label information.
First, we will start by importing the necessary packages:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
Next, load the digit dataset from sklearn and make an object of it. We can also find number
of rows and columns in this dataset as follows:
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
Output
(1797, 64)
The above output shows that this dataset is having 1797 samples with 64 features.
We can perform the clustering as we did in Example 1 above:
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
Output
(10, 64)
The above output shows that K-means created 10 clusters with 64 features.
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)
118
Machine Learning with Python
Output
As output, we will get following image showing clusters centers learned by k-means.
The following lines of code will match the learned cluster labels with the true labels found
in them:
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
Next, we can check the accuracy as follows:
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)
Output
0.7935447968836951
The above output shows that the accuracy is around 80%.
Advantages and Disadvantages
Advantages
The following are some advantages of K-Means clustering algorithms:
It is very easy to understand and implement.
If we have large number of variables then, K-means would be faster than
Hierarchical clustering.
On re-computation of centroids, an instance can change the cluster.
Tighter clusters are formed with K-means as compared to Hierarchical clustering.
Disadvantages:
119
Machine Learning with Python
The following are some disadvantages of K-Means clustering algorithms:
It is a bit difficult to predict the number of clusters i.e. the value of k.
Output is strongly impacted by initial inputs like number of clusters (value of k)
Order of data will have strong impact on the final output.
It is very sensitive to rescaling. If we will rescale our data by means of
normalization or standardization, then the output will completely change.
It is not good in doing clustering job if the clusters have a complicated geometric
shape.
Applications of K-Means Clustering Algorithm
The main goals of cluster analysis are:
To get a meaningful intuition from the data we are working with.
Cluster-then-predict where different models will be built for different subgroups.
To fulfill the above-mentioned goals, K-means clustering is performing well enough. It can
be used in following applications:
Market segmentation
Document Clustering
Image segmentation
Image compression
Customer segmentation
Analyzing the trend on dynamic data