机器学习Python教程
引言
在上一章中,我们推导了计算文档 d 属于类别或类 c 的概率的公式,表示为 P(c∣d)。
我们已将许多论著中使用的 P(c∣d) 标准公式转化为数值稳定的形式。
我们将在 Python 中实现朴素贝叶斯分类器。朴素贝叶斯方法的正式介绍可以在我们上一章中找到。
Python 因其强大的字符串类和方法,以及正则表达式模块 re 提供的超越其他编程语言的工具,而非常适合文本分类。
唯一的缺点可能是此 Python 实现未针对效率进行优化。
上一章的 Python 实现
文档表示
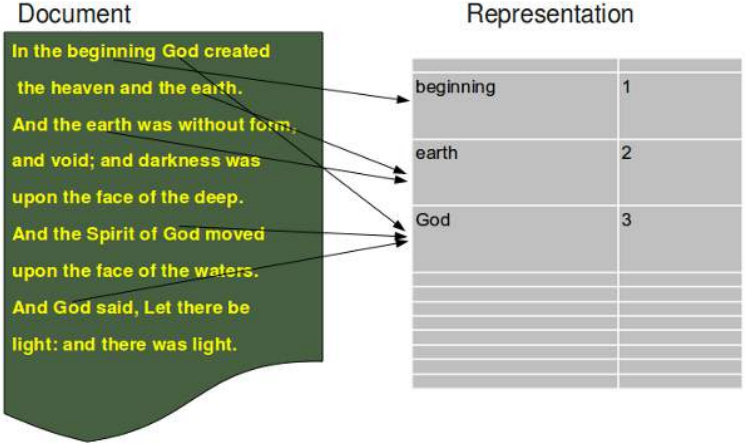
基于词袋模型的文档表示如下图所示:
所需的导入
我们的实现需要正则表达式模块 re 和 os 模块:
import re
import os
我们将在实现中使用我们关于字典那一章的练习 1 中的 dict_merge_sum 函数:
def dict_merge_sum(d1, d2):
""" 两个字典 d1 和 d2 具有数值,并且
可能具有不相交的键。如果键同时存在于两个字典中,则其值相加,
否则,缺失的值被视为 0。
"""
return { k: d1.get(k, 0) + d2.get(k, 0) for k in set(d1) | set(d2) }
d1 = dict(a=4, b=5, d=8)
d2 = dict(a=1, d=10, e=9)
print(dict_merge_sum(d1, d2))
Output:
{'e': 9, 'd': 18, 'b': 5, 'a': 5}
BAGOFWORDSCLASS
class BagOfWords(object):
""" 实现词袋,单词及其在“文档”中的使用频率,
供 Document 类、Category 类和 Pool 类使用。
"""
def __init__(self):
self.__number_of_words = 0
self.__bag_of_words = {}
def __add__(self, other):
""" 重载“+”运算符以连接两个 BagOfWords """
erg = BagOfWords()
erg.__bag_of_words = dict_merge_sum(self.__bag_of_words,
other.__bag_of_words)
return erg
def add_word(self, word):
""" 将一个单词添加到字典 __bag_of_words 中 """
self.__number_of_words += 1
if word in self.__bag_of_words:
self.__bag_of_words[word] += 1
else:
self.__bag_of_words[word] = 1
def len(self):
""" 返回对象中不同单词的数量 """
return len(self.__bag_of_words)
def Words(self):
""" 返回对象中包含的单词列表 """
return self.__bag_of_words.keys()
def BagOfWords(self):
""" 返回字典,包含单词(键)及其频率(值)"""
return self.__bag_of_words
def WordFreq(self, word):
""" 返回一个单词的频率 """
if word in self.__bag_of_words:
return self.__bag_of_words[word]
else:
return 0
DOCUMENT 类
class Document(object):
""" 用于学习(训练)文档和测试文档。
如果要训练分类器,可选参数 learn 必须设置为 True。
如果是测试文档,learn 必须设置为 False。
"""
_vocabulary = BagOfWords() # 类变量,用于存储所有文档的词汇表
def __init__(self, vocabulary):
self.__name = ""
self.__document_class = None
self._words_and_freq = BagOfWords()
Document._vocabulary = vocabulary # 将传入的词汇表赋给类变量
def read_document(self, filename, learn=False):
""" 读取文档。假定文档编码为 utf-8 或 iso-8859... (latin-1)。
文档中的单词存储在一个词袋中,即 self._words_and_freq = BagOfWords()
"""
try:
text = open(filename, "r", encoding='utf-8').read()
except UnicodeDecodeError:
text = open(filename, "r", encoding='latin-1').read()
text = text.lower()
words = re.split(r"\W+", text) # 使用 \W+ 处理多个非字母字符
# self._number_of_words = 0 # 这行似乎是多余的,BagOfWords内部管理
for word in words:
if word: # 过滤空字符串,re.split可能会产生
self._words_and_freq.add_word(word)
if learn:
Document._vocabulary.add_word(word)
def __add__(self, other):
""" 重载“+”运算符。添加两个文档在于添加文档的词袋。 """
res = Document(Document._vocabulary)
res._words_and_freq = self._words_and_freq + other._words_and_freq
return res
def vocabulary_length(self):
""" 返回词汇表的长度 """
return Document._vocabulary.len()
def WordsAndFreq(self):
""" 返回字典,包含文档的 BagOfWords 属性中包含的单词(键)及其频率(值)"""
return self._words_and_freq.BagOfWords()
def Words(self):
""" 返回 Document 对象的单词 """
d = self._words_and_freq.BagOfWords()
return list(d.keys()) # 确保返回列表
def WordFreq(self, word):
""" 返回单词“word”在文档中出现的次数 """
bow = self._words_and_freq.BagOfWords()
if word in bow:
return bow[word]
else:
return 0
def __and__(self, other):
""" 两个文档的交集。返回在两个文档中都出现的单词列表。 """
intersection = []
words1 = set(self.Words()) # 使用集合进行更高效的查找
for word in other.Words():
if word in words1:
intersection.append(word)
return intersection
CATEGORY / COLLECTIONS OF DOCUMENTS
这是由一个类别/类别的文档组成的类。我们使用术语“类别”而不是“类”,以免与 Python 类混淆:
class Category(Document):
def __init__(self, vocabulary):
super().__init__(vocabulary) # 使用 super() 调用父类构造函数
self._number_of_docs = 0
def Probability(self, word):
""" 返回给定类别“self”的单词“word”的概率 """
# 这里可能需要根据贝叶斯分类器的具体公式进行调整
# 这个实现似乎更像是计算一个词在给定类别中的平滑频率
voc_len = Document._vocabulary.len()
# SumN = 0 # 这一行是多余的
# for i in range(voc_len): # 这段循环是错误的,SumN 应该只取决于 word
SumN = Category._vocabulary.WordFreq(word) # 单词在总词汇表中的频率
N = self._words_and_freq.WordFreq(word) # 单词在该类别中的频率
# 使用拉普拉斯平滑(加 1 平滑)
erg = 1 + N
erg /= voc_len + SumN
return erg
def __add__(self, other):
""" 重载“+”运算符。添加两个 Category 对象在于添加 Category 对象的词袋。 """
res = Category(self._vocabulary)
res._words_and_freq = self._words_and_freq + other._words_and_freq
return res
def SetNumberOfDocs(self, number):
self._number_of_docs = number
def NumberOfDocuments(self):
return self._number_of_docs
THE POOL CLASS
Pool 是训练和保存文档类的类:
class Pool(object):
def __init__(self):
self.__document_classes = {}
self.__vocabulary = BagOfWords()
def sum_words_in_class(self, dclass_name): # 更改参数名为 dclass_name
""" 类别中所有不同单词出现的总次数 """
sum_val = 0 # 避免使用内置函数名 sum
# 确保 dclass_name 存在于 self.__document_classes 中
if dclass_name in self.__document_classes:
for word in self.__vocabulary.Words():
WaF = self.__document_classes[dclass_name].WordsAndFreq()
if word in WaF:
sum_val += WaF[word]
return sum_val
def learn(self, directory, dclass_name):
""" directory 是一个路径,可以在其中找到名为 dclass_name 的类文件 """
x = Category(self.__vocabulary)
dir_files = os.listdir(directory) # 更改变量名以避免与内置函数冲突
docs_in_category = [] # 用于收集该类别的所有文档
for file in dir_files:
d = Document(self.__vocabulary)
# print(directory + "/" + file) # 调试用,可取消注释
d.read_document(os.path.join(directory, file), learn=True) # 使用 os.path.join
docs_in_category.append(d) # 添加到列表
# 将所有文档的词袋合并到类别中
if docs_in_category:
x._words_and_freq = sum([doc._words_and_freq for doc in docs_in_category], BagOfWords())
self.__document_classes[dclass_name] = x
x.SetNumberOfDocs(len(dir_files))
def Probability(self, doc_path, dclass_name=""): # 更改参数名为 doc_path, dclass_name
""" 计算给定文档 doc_path 属于类别 dclass_name 的概率 """
d = Document(self.__vocabulary)
d.read_document(doc_path)
if not dclass_name: # 如果没有指定具体类别,则返回所有类别的概率列表
prob_list = []
for current_dclass_name in self.__document_classes:
prob = self.Probability(doc_path, current_dclass_name) # 递归调用
if prob != -1: # 避免添加 -1 结果
prob_list.append([current_dclass_name, prob])
# 对概率进行归一化,如果总和不为 0
total_prob = sum(p[1] for p in prob_list)
if total_prob > 0:
prob_list = [[p[0], p[1] / total_prob] for p in prob_list]
elif prob_list: # 如果总和为 0 但列表不为空,则平均分配
num_classes = len(prob_list)
prob_list = [[p[0], 1.0 / num_classes] for p in prob_list]
prob_list.sort(key = lambda x: x[1], reverse = True)
return prob_list
else: # 计算特定类别的概率 P(c_j | d_i)
# P(c_j | d_i) = P(d_i | c_j) * P(c_j) / P(d_i)
# 我们将使用 log-probabilities 来避免浮点数下溢
# log(P(c_j))
num_docs_cj = self.__document_classes[dclass_name].NumberOfDocuments()
total_docs = sum(c.NumberOfDocuments() for c in self.__document_classes.values())
if total_docs == 0: # 避免除以零
return -1
log_prior_cj = np.log(num_docs_cj / total_docs) if num_docs_cj > 0 else -np.inf
# log(P(d_i | c_j)) = sum(log(P(w_k | c_j)))
log_likelihood = 0.0
# 获取当前类别的词袋
dclass_bow = self.__document_classes[dclass_name]._words_and_freq
# 类别中单词总数(用于平滑)
sum_words_in_current_class = self.sum_words_in_class(dclass_name)
# 词汇表大小
vocab_len = self.__vocabulary.len()
for word in d.Words():
# 单词在当前类别中的频率 (N_tC)
word_freq_in_class = dclass_bow.WordFreq(word)
# 拉普拉斯平滑:P(w_t | c_j) = (N_tC + 1) / (sum(N_kC) + vocab_size)
# 这里 sum(N_kC) 是类别中所有单词的总数 (sum_words_in_current_class)
# 并且 vocab_size 是总词汇量 (vocab_len)
# P(word | class)
p_word_given_class = (word_freq_in_class + 1) / (sum_words_in_current_class + vocab_len)
if p_word_given_class > 0:
log_likelihood += np.log(p_word_given_class)
else:
# 如果概率为0,则这会导致 log(0) 为 -inf,从而整个概率为 0
# 对于贝叶斯,通常平滑会防止这种情况,但以防万一
log_likelihood = -np.inf
break
# 总对数概率 log(P(c_j | d_i)) = log(P(d_i | c_j)) + log(P(c_j)) - log(P(d_i))
# P(d_i) 是归一化因子,在比较时可以省略
# 返回 e^(log_prior_cj + log_likelihood)
# 直接返回未归一化的 P(c_j) * P(d_i | c_j)
# 在没有提供 dclass_name 时,会在外部进行归一化
# 简化计算,根据公式 P(c_j | d_i) = P(d_i | c_j) * P(c_j) / P(d_i)
# 我们只计算 P(d_i | c_j) * P(c_j) 并让外部归一化
# 这里是您原始的实现逻辑,它计算的是 P(d_i) / (P(d_i | c_j) * P(c_j))
# 这是一个反向的概率计算,需要调整
# 我们重新实现基于标准贝叶斯分类的概率计算
# P(c_j | d_i) = P(c_j) * Product(P(w_k | c_j))
# 计算 P(c_j)
prob_cj = num_docs_cj / total_docs if total_docs > 0 else 0
# 计算 Product(P(w_k | c_j))
product_prob_words = 1.0
# 对于文档中的每个单词
for word in d.Words():
word_freq_in_class = dclass_bow.WordFreq(word)
# 应用拉普拉斯平滑
p_word_given_class_smooth = (word_freq_in_class + 1) / (sum_words_in_current_class + vocab_len)
product_prob_words *= p_word_given_class_smooth
# 最终的未归一化概率
unnormalized_prob = prob_cj * product_prob_words
return unnormalized_prob
def DocumentIntersectionWithClasses(self, doc_name):
res = [doc_name]
for dc in self.__document_classes:
d = Document(self.__vocabulary)
d.read_document(doc_name, learn=False)
o = self.__document_classes[dc] & d
# 避免除以零
len_d_words = len(d.Words())
if len_d_words > 0:
intersection_ratio = len(o) / len_d_words
else:
intersection_ratio = 0 # 如果文档没有单词,交集比率为 0
res.append((dc, intersection_ratio)) # 将元组添加到列表中,而不是 +=
return res
使用分类器
为了能够训练和测试分类器,我们提供了一个“可下载的学习和测试集”。NaiveBayes 模块包含我们目前提供的代码,但为了方便,可以下载为 NaiveBayes.py。学习和测试集包含标记为六个类别(“clinton”、“lawyer”、“math”、“medical”、“music”、“sex”)的(旧)笑话。
import os
DClasses = ["clinton",
"lawyer",
"math",
"medical",
"music",
"sex"]
base = "data/jokes/learn/"
p = Pool()
for dclass in DClasses:
p.learn(base + dclass, dclass)
base = "data/jokes/test/"
results = []
for dclass in DClasses:
# 确保目录存在且可访问
current_dir = os.path.join(base, dclass)
if os.path.isdir(current_dir):
dir_files = os.listdir(current_dir)
for file in dir_files:
file_path = os.path.join(current_dir, file)
res = p.Probability(file_path)
results.append(f"{dclass}: {file}: {str(res)}")
else:
print(f"Warning: Directory not found or not accessible: {current_dir}")
print(results[:10])
Output:
["clinton: clinton13.txt: [['clinton', 0.9999999999994136], ['lawyer', 4.836910173924097e-13], ['medical', 1.0275816932480502e-13], ['sex', 2.259655644772941e-20], ['music', 1.9461534629330693e-23], ['math', 1.555345744116502e-26]]", "clinton: clinton53.txt: [['clinton', 1.0], ['medical', 9.188673872554947e-27], ['lawyer', 1.8427106994083583e-27], ['sex', 1.5230675259429155e-27], ['music', 1.1695224390877453e-31], ['math', 1.1684669623309053e-33]]", "clinton: clinton43.txt: [['clinton', 0.9999999931196475], ['lawyer', 5.860057747465498e-09], ['medical', 9.607574904397297e-10], ['sex', 5.894524557321511e-11], ['music', 3.7727719397911977e-13], ['math', 2.147560501376133e-13]]", "clinton: clinton3.txt: [['clinton', 0.9999999999999962], ['music', 2.2781994419060397e-15], ['medical', 1.1698375401225822e-15], ['lawyer', 4.527194012614925e-16], ['sex', 1.5454131826930606e-17], ['math', 7.079852963638893e-18]]", "clinton: clinton33.txt: [['clinton', 0.9999999999990845], ['sex', 4.541025305456911e-13], ['lawyer', 3.126691883689181e-13], ['medical', 1.3677618519146697e-13], ['music', 1.2066374685712134e-14], ['math', 7.905002788169863e-19]]", "clinton: clinton23.txt: [['clinton', 0.9999999990044788], ['music', 9.903297627375497e-10], ['lawyer', 4.599127712898122e-12], ['math', 5.204515552253461e-13], ['sex', 6.840062626646056e-14], ['medical', 3.2400016635923044e-15]]", "lawyer: lawyer203.txt: [['lawyer', 0.9786187307635054], ['music', 0.009313838824293683], ['clinton', 0.007226994270357742], ['sex', 0.004650195377700058], ['medical', 0.00019018203662436446], ['math', 5.87275188878159e-08]]", "lawyer: lawyer233.txt: [['music', 0.7468245708838688], ['lawyer', 0.2505817879364303], ['clinton', 0.0025913149343268467], ['medical', 1.71345437802292e-06], ['sex', 6.081558428153343e-07], ['math', 4.635153054869146e-09]]", "lawyer: lawyer273.txt: [['clinton', 1.0], ['lawyer', 3.1987559043152286e-46], ['music', 1.3296257614591338e-54], ['math', 9.431988300101994e-85], ['sex', 3.1890112632916554e-91], ['medical', 1.5171123775659174e-99]]", "lawyer: lawyer213.txt: [['lawyer', 0.9915688655897351], ['music', 0.005065592126015617], ['clinton', 0.003206989396712446], ['math', 6.94882106646087e-05], ['medical', 6.923689581139796e-05], ['sex', 1.982778106069595e-05]]"]
注释
-
请参阅我们上一章的“延伸阅读”部分。
INTRODUCTION
In the previous chapter, we have deduced the formula for calculating the
probability that a document d belongs to a category or class c, denoted as
P(c|d).
We have transformed the standard formular for P(c|d), as it is used in many
treatises1, into a numerically stable form.
We use a Naive Bayes classifier for our implementation in Python. The
formal introduction into the Naive Bayes approach can be found in our
previous chapter.
Python is ideal for text classification, because of it's strong string class with
powerful methods. Furthermore the regular expression module re of Python
provides the user with tools, which are way beyond other programming
languages.
The only downside might be that this Python implementation is not tuned
for efficiency.
PYTHON IMPLEMENTATION OF PREVIOUS CHAPTER
DOCUMENT REPRESENTATION
The document representation, which is based on the bag of word model, is illustrated in the following
diagram:
327
IMPORTS NEEDED
Our implementation needs the regular expression module re and the os module:
importimportre
os
We will use in our implementation the function dict_merge_sum from the exercise 1 of our chapter on
dictionaries:
def dict_merge_sum(d1, d2):
""" Two dicionaries d1 and d2 with numerical values and
possibly disjoint keys are merged and the values are added if
the exist in both values, otherwise the missing value is take
n to
be 0"""
return { k: d1.get(k, 0) + d2.get(k, 0) for k in set(d1) | se
t(d2) }
d1 = dict(a=4, b=5, d=8)
328
d2 = dict(a=1, d=10, e=9)
dict_merge_sum(d1, d2)
Output:{'e': 9, 'd': 18, 'b': 5, 'a': 5}
BAGOFWORDSCLASS
class BagOfWords(object):
""" Implementing a bag of words, words corresponding with thei
r
frequency of usages in a "document" for usage by the
Document class, Category class and the Pool class."""
def __init__(self):
self.__number_of_words = 0
self.__bag_of_words = {}
def __add__(self, other):
""" Overloading of the "+" operator to join two BagOfWord
s """
erg = BagOfWords()
erg.__bag_of_words = dict_merge_sum(self.__bag_of_words,
other.__bag_of_words)
return erg
def add_word(self,word):
""" A word is added in the dictionary __bag_of_words"""
self.__number_of_words += 1
if word in self.__bag_of_words:
self.__bag_of_words[word] += 1
else:
self.__bag_of_words[word] = 1
def len(self):
""" Returning the number of different words of an object
"""
return len(self.__bag_of_words)
def Words(self):
""" Returning a list of the words contained in the object
"""
return self.__bag_of_words.keys()
329
def BagOfWords(self):
""" Returning the dictionary, containing the words (keys)
with their frequency (values)"""
return self.__bag_of_words
def WordFreq(self,word):
""" Returning the frequency of a word """
if word in self.__bag_of_words:
return self.__bag_of_words[word]
else:
return 0
THE DOCUMENT CLASS
class Document(object):
""" Used both for learning (training) documents and for testin
g documents. The optional parameter lear
has to be set to True, if a classificator should be trained. I
f it is a test document learn has to be set to False. """
_vocabulary = BagOfWords()
def __init__(self, vocabulary):
self.__name = ""
self.__document_class = None
self._words_and_freq = BagOfWords()
Document._vocabulary = vocabulary
def read_document(self,filename, learn=False):
""" A document is read. It is assumed that the document i
s either encoded in utf-8 or in iso-8859... (latin-1).
The words of the document are stored in a Bag of Words,
i.e. self._words_and_freq = BagOfWords() """
try:
text = open(filename,"r", encoding='utf-8').read()
except UnicodeDecodeError:
text = open(filename,"r", encoding='latin-1').read()
text = text.lower()
words = re.split(r"\W",text)
self._number_of_words = 0
for word in words:
self._words_and_freq.add_word(word)
if learn:
330
Document._vocabulary.add_word(word)
def __add__(self,other):
""" Overloading the "+" operator. Adding two documents con
sists in adding the BagOfWords of the Documents """
res = Document(Document._vocabulary)
res._words_and_freq = self._words_and_freq + other._word
s_and_freq
return res
def vocabulary_length(self):
""" Returning the length of the vocabulary """
return len(Document._vocabulary)
def WordsAndFreq(self):
""" Returning the dictionary, containing the words (keys)
with their frequency (values) as contained
in the BagOfWords attribute of the document"""
return self._words_and_freq.BagOfWords()
def Words(self):
""" Returning the words of the Document object """
d = self._words_and_freq.BagOfWords()
return d.keys()
def WordFreq(self,word):
""" Returning the number of times the word "word" appeare
d in the document """
bow = self._words_and_freq.BagOfWords()
if word in bow:
return bow[word]
else:
return 0
def __and__(self, other):
""" Intersection of two documents. A list of words occurin
g in both documents is returned """
intersection = []
words1 = self.Words()
for word in other.Words():
if word in words1:
intersection += [word]
return intersection
331
CATEGORY / COLLECTIONS OF DOCUMENTS
This is the class consisting of the documents for one category /class. We use the term category instead of
"class" so that it will not be confused with Python classes:
class Category(Document):
def __init__(self, vocabulary):
Document.__init__(self, vocabulary)
self._number_of_docs = 0
def Probability(self,word):
""" returns the probabilty of the word "word" given the cl
ass "self" """
voc_len = Document._vocabulary.len()
SumN = 0
for i in range(voc_len):
SumN = Category._vocabulary.WordFreq(word)
N = self._words_and_freq.WordFreq(word)
erg = 1 + N
erg /= voc_len + SumN
return erg
def __add__(self,other):
""" Overloading the "+" operator. Adding two Category obje
cts consists in adding the
BagOfWords of the Category objects """
res = Category(self._vocabulary)
res._words_and_freq = self._words_and_freq + other._word
s_and_freq
return res
def SetNumberOfDocs(self, number):
self._number_of_docs = number
defNumberOfDocuments(self):
return self._number_of_docs
THE POOL CLASS
The pool is the class, where the document classes are trained and kept:
class Pool(object):
def __init__(self):
332
self.__document_classes = {}
self.__vocabulary = BagOfWords()
def sum_words_in_class(self, dclass):
""" The number of times all different words of a dclass ap
pear in a class """
sum = 0
for word in self.__vocabulary.Words():
WaF = self.__document_classes[dclass].WordsAndFreq()
if word in WaF:
sum += WaF[word]
return sum
def learn(self, directory, dclass_name):
""" directory is a path, where the files of the class wit
h the name dclass_name can be found """
x = Category(self.__vocabulary)
dir = os.listdir(directory)
for file in dir:
d = Document(self.__vocabulary)
#print(directory + "/" + file)
d.read_document(directory + "/" + file, learn = True)
x = x + d
self.__document_classes[dclass_name] = x
x.SetNumberOfDocs(len(dir))
def Probability(self, doc, dclass = ""):
"""Calculates the probability for a class dclass given a d
ocument doc"""
if dclass:
sum_dclass = self.sum_words_in_class(dclass)
prob = 0
d = Document(self.__vocabulary)
d.read_document(doc)
for j in self.__document_classes:
sum_j = self.sum_words_in_class(j)
prod = 1
for i in d.Words():
wf_dclass = 1 + self.__document_classes[dclas
s].WordFreq(i)
wf = 1 + self.__document_classes[j].WordFre
q(i)
333
r = wf * sum_dclass / (wf_dclass * sum_j)
prod *= r
prob += prod * self.__document_classes[j].NumberOf
Documents() / self.__document_classes[dclass].NumberOfDocuments()
if prob != 0:
return 1 / prob
else:
return -1
else:
prob_list = []
for dclass in self.__document_classes:
prob = self.Probability(doc, dclass)
prob_list.append([dclass,prob])
prob_list.sort(key = lambda x: x[1], reverse = True)
return prob_list
def DocumentIntersectionWithClasses(self, doc_name):
res = [doc_name]
for dc in self.__document_classes:
d = Document(self.__vocabulary)
d.read_document(doc_name, learn=False)
o = self.__document_classes[dc] & d
intersection_ratio = len(o) / len(d.Words())
res += (dc, intersection_ratio)
return res
USING THE CLASSIFIER
To be able to learn and test a classifier, we offer a "Learn and test set to Download". The module NaiveBayes
consists of the code we have provided so far, but it can be downloaded for convenience as NaiveBayes.py The
learn and test sets contain (old) jokes labelled in six categories: "clinton", "lawyer", "math", "medical",
"music", "sex".
import os
DClasses = ["clinton",
"lawyer",
"math",
"medical",
"music",
"sex"]
base = "data/jokes/learn/"
p = Pool()
for dclass in DClasses:
p.learn(base + dclass, dclass)
334
base = "data/jokes/test/"
results = []
for dclass in DClasses:
dir = os.listdir(base + dclass)
for file in dir:
res = p.Probability(base + dclass + "/" + file)
results.append(f"{dclass}: {file}: {str(res)}")
print(results[:10])
["clinton: clinton13.txt: [['clinton', 0.9999999999994136], ['lawy
er', 4.836910173924097e-13], ['medical', 1.0275816932480502e-13],
['sex', 2.259655644772941e-20], ['music', 1.9461534629330693e-2
3], ['math', 1.555345744116502e-26]]", "clinton: clinton53.txt:
[['clinton', 1.0], ['medical', 9.188673872554947e-27], ['lawyer',
1.8427106994083583e-27], ['sex', 1.5230675259429155e-27], ['musi
c', 1.1695224390877453e-31], ['math', 1.1684669623309053e-33]]",
"clinton: clinton43.txt: [['clinton', 0.9999999931196475], ['lawye
r', 5.860057747465498e-09], ['medical', 9.607574904397297e-10],
['sex', 5.894524557321511e-11], ['music', 3.7727719397911977e-1
3], ['math', 2.147560501376133e-13]]", "clinton: clinton3.txt:
[['clinton', 0.9999999999999962], ['music', 2.2781994419060397e-1
5], ['medical', 1.1698375401225822e-15], ['lawyer', 4.527194012614
925e-16], ['sex', 1.5454131826930606e-17], ['math', 7.079852963638
893e-18]]", "clinton: clinton33.txt: [['clinton', 0.99999999999908
45], ['sex', 4.541025305456911e-13], ['lawyer', 3.126691883689181
e-13], ['medical', 1.3677618519146697e-13], ['music', 1.2066374685
712134e-14], ['math', 7.905002788169863e-19]]", "clinton: clinton2
3.txt: [['clinton', 0.9999999990044788], ['music', 9.9032976273754
97e-10], ['lawyer', 4.599127712898122e-12], ['math', 5.20451555225
3461e-13], ['sex', 6.840062626646056e-14], ['medical', 3.240001663
5923044e-15]]", "lawyer: lawyer203.txt: [['lawyer', 0.978618730763
5054], ['music', 0.009313838824293683], ['clinton', 0.007226994270
357742], ['sex', 0.004650195377700058], ['medical', 0.000190182036
62436446], ['math', 5.87275188878159e-08]]", "lawyer: lawyer233.tx
t: [['music', 0.7468245708838688], ['lawyer', 0.250581787936430
3], ['clinton', 0.0025913149343268467], ['medical', 1.713454378022
92e-06], ['sex', 6.081558428153343e-07], ['math', 4.63515305486914
6e-09]]", "lawyer: lawyer273.txt: [['clinton', 1.0], ['lawyer',
3.1987559043152286e-46], ['music', 1.3296257614591338e-54], ['mat
h', 9.431988300101994e-85], ['sex', 3.1890112632916554e-91], ['med
ical', 1.5171123775659174e-99]]", "lawyer: lawyer213.txt: [['lawye
r', 0.9915688655897351], ['music', 0.005065592126015617], ['clinto
n', 0.003206989396712446], ['math', 6.94882106646087e-05], ['medic
al', 6.923689581139796e-05], ['sex', 1.982778106069595e-05]]"]
335
FOOTNOTES
1
Please see our "Further Reading" section of our previous chapter