章节大纲

  • Vector Addition
    ::矢量加进

    Adding in Two Dimensions
    ::在两个维中添加

    In the following image, vectors  A and  B represent the two displacements of a person who walked 90. m east and then 50. m north.  We want to add these two vectors to get the vector sum of the two movements.
    ::在下图中,矢量A和矢量B代表一个人在东行90米,北行50米的两次迁移。我们要加上这两个矢量,以获得两种移动的矢量总和。

    Graphical representation of adding two vectors: 90 m east and 50 m north.

    The graphical process for adding vectors in two dimensions is to place the tail of the second vector on the arrow head of the first vector as shown above.
    ::在两个维度中添加矢量的图形进程是将第二个矢量的尾部置于上面所示第一个矢量的箭头上。

    The sum of the two vectors is the vector that begins at the origin of the first vector and goes to the ending of the second vector, as shown below.
    ::两个矢量的总和是始于第一个矢量来源的矢量,然后到第二个矢量终点的矢量,如下文所示。

    Two vectors representing two displacements of a person who walked 90 mi east and then 50 mi north, with the third vector connecting the two, creating a triangle indicating the sum

    If we are using totally graphic means of adding these vectors, the magnitude of the sum can be determined by measuring the length of the sum vector and comparing it to the original standard. We then use a compass to measure the angle of the summation vector.
    ::如果我们使用完全图形手段来添加这些矢量,那么总和的大小可以通过测量总矢量的长度并将其与原始标准进行比较来确定。然后我们用一个指南针来测量总和矢量的角。

    If we are using calculation, we first determine the inverse tangent of 50 units divided by 90 units and get the angle of 29° north of east. The length of the sum vector can then be determined mathematically by the Pythagorean theorem,  a 2 + b 2 = c 2 .  In this case, the length of the hypotenuse would be the square root of (8100 + 2500), or 103 units.
    ::如果我们使用计算法, 我们首先确定 50 个单位的反正切值除以 90 个单位, 然后取向以东 29 ° 的角。 然后, 该矢量的总长度可以由 Pythagorean 定理, a2+b2=c2 数学确定。 在这种情况下, 下限的长度将是 平方根( 8100 + 2500 ) 或 103 个单位的平方根 。

    If three or four vectors are to be added by graphical means, we would continue to place each new vector head to toe with the vectors to be added until all the vectors were in the coordinate system. The resultant, or sum, vector would be the vector from the origin of the first vector to the arrowhead of the last vector; the magnitude and direction of this sum vector would then be measured.
    ::如果用图形手段添加三或四个矢量,我们将继续将每个新的矢量头与矢量联在一起,直到所有矢量都在坐标系统中。由此产生的矢量或总值将是从第一个矢量的起源到最后一个矢量的箭头的矢量;然后将测量该总矢量的大小和方向。

    Mathematical Methods of Vector Addition
    ::矢量添加数学方法

    We can add vectors mathematically using trig functions, the law of cosines, or the Pythagorean theorem.
    ::我们可以使用三角函数, 共弦定律, 或毕达哥伦定理, 以数学方式添加矢量。

    If the vectors to be added are at right angles to each other, such as the example above, we would assign them to the sides of a right triangle and calculate the sum as the hypotenuse of the right triangle. We would also calculate the direction of the sum vector by using an inverse sin or some other trig function.
    ::如果要添加的矢量位于彼此的正确角度上,例如上面的例子,我们将把它们分配到右三角的两边,并将总和计算为右三角的下限。我们还将使用反罪或其它三角函数来计算矢量的总和方向。

    Suppose, however, that we wish to add two vectors that are not at right angles to each other. Let’s consider the vectors in the following images.
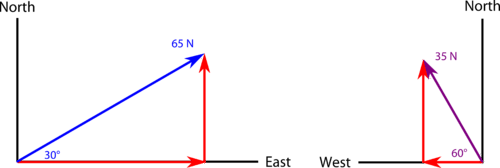
    ::然而,假设我们想添加两个不正确角度的矢量。 让我们在下面的图像中考虑矢量。

    Two vectors are illustrated with their magnitudes and angles relative to cardinal directions.

    The two vectors we are to add are a force of 65 N at 30° north of east and a force of 35 N at 60° north of west.
    ::我们要补充的两个矢量是东纬30度以北65牛顿,西经60度以北35牛顿。

    We know that vectors in the same dimension can be added by regular arithmetic. Therefore, we can resolve each of these vectors into components that lay on the axes as pictured below. The  resolution of vectors  reduces each vector to a component on the north-south axis and a component on the east-west axis. 
    ::我们知道,同一维度的矢量可以通过正常的算术来添加。 因此, 我们可以将这些矢量中的每一个解析成如下图所示的轴上的组件。 矢量的分辨率将每个矢量降低为南北轴上的组件和东西轴上的组件。


    Vectors representing forces at specific angles, illustrating their resolution into components.

    After resolving each vector into two components, we can now mathematically determine the magnitude of the components. Once we have done that, we can add the components in the same direction arithmetically. This will give us two vectors that are perpendicular to each other and can be the legs of a right triangle.
    ::在将每个矢量分解成两个组成部分后, 我们现在可以用数学来决定组件的大小。 一旦我们这样做了, 我们可以用算法将组件添加到同一个方向上。 这将给我们提供两个相互垂直的矢量, 并且可以是右三角形的腿 。

    The east-west component of the first vector is (65 N)(cos 30°) = (65 N)(0.866) = 56.3 N  east
    ::第一个向量的东-西部分是(65牛顿(30°)(65牛顿)(0.866)=56.3牛顿(东经)(65牛顿)(30°)=(65牛顿)(0.866)=56.3牛顿(东经)。

    The north-south component of the first vector is (65 N)(sin 30°) = (65 N)(0.500) = 32.5 N north
    ::第一个矢量的北向-南部分为(65牛顿)(30°)(65牛顿)(0.500)=32.5牛顿(北纬)=(65牛顿)(30°)(65牛顿)(0.500)=32.5牛顿)。

    The east-west component of the second vector is (35 N)(cos 60°) = (35 N)(0.500) = 17.5 N west
    ::第二个矢量的东-西部分为(35牛顿)(60°)=(35牛顿)(0.500)=17.5牛顿西部。

    The north-south component of the second vector is (35 N)(sin 60°) = (35 N)(0.866) = 30.3 N north
    ::第二个矢量的北向-南部分为(35牛顿(60°)(sin 60°)=(35牛顿(0.866)=30.3牛顿(北部))

    The sum of the two east-west components is 56.3 N - 17.5 N = 38.8 N east
    ::东-西两个组成部分的总和为56.3 N-17.5 N=38.8 N东部

    The sum of the two north-south components is 32.5 N + 30.3 N = 62.8 N north
    ::两个南北构成部分的总和是32.5 N+30.3 N=62.8 N北部

    We can now consider those two vectors to be the sides of a right triangle and find the length and direction of the hypotenuse using the Pythagorean Theorem and trig functions.
    ::我们现在可以把这两种矢量视为右三角形的两边,并使用毕达哥伦理论和三角函数来找到下层的长度和方向。

    c = √ 38.8 2 + 62.8 2 = 74   N
    ::c38.82+62.82=74 N

    sin   x = 62.8 74   so   x = sin − 1 0.84   so   x = 58 ∘
    ::x=62.874 so x=sin- 10.84 so x=58

    The direction of the sum vector is 74 N at 58° north of east.
    ::向量总方向为东面以北58度时74牛顿。

    Perpendicular vectors have no components in the other direction. For example, if a boat is floating down a river due south, and you are paddling the boat due east, the eastward vector has no component in the north-south direction and therefore, has no effect on the north-south motion. If the boat is floating down the river at 5 mph south and you paddle the boat eastward at 5 mph, the boat continues to float southward at 5 mph. The eastward motion has absolutely no effect on the southward motion. Perpendicular vectors have NO effect on each other.
    ::垂直矢量在另一方向没有组件。例如,如果一艘船只漂浮在向南的一条河流上,而你正在向东划船,则向东的矢量在南北方向没有部件,因此对北南运动没有影响。如果船只在南面5米处漂浮,然后在南面5米处向东划船,则船只继续向南向南航行,在5米处向南航行。向东运动对向南运动完全没有影响。垂直矢量对对方没有影响。

    Examples
    ::实例

    A motorboat heads due east at 16 m/s across a river that flows due north at 9.0 m/s.
    ::一艘机动艇在16米/秒/秒时向东驶过一条以9.0米/秒向北流动的河流。

    Example 1
    ::例1

    What is the resultant of the boat?
    ::船的产物是什么?

    Sketch:
    ::箭头 :

    Right triangle showing boat and current velocities with resultant vector labeled.

    Since the two motions are perpendicular to each other, they can be assigned to the legs of a right triangle and the hypotenuse (resultant) calculated.
    ::由于这两项动议是相互切合的,因此可以分配给右三角的腿和计算下限(结果)。

    c = √ a 2 + b 2 = √ ( 16   m/s ) 2 + ( 9.0   m/s ) 2 = 18   m/s
    ::ca2+b2(16 m/s)2+(9.0 m/s)2=18 m/s

    sin θ = 9.0 18 = 0.500   and therefore   θ = 30 ∘
    ::9,018=0.500,因此,_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

    The resultant is 18 m/s at 30° north of east.
    ::其结果为东部以北30度时每秒18米。

    Example 2
    ::例2

    If the river is 135 m wide, how long does it take the boat to reach the other side?
    ::如果河宽135米,船要多久才能到达另一边?

    The boat is traveling across the river at 16 m/s due to the motor.  The current is perpendicular and therefore has no effect on the across the river.  The time required for the trip can be determined by dividing the by the velocity.
    ::由于马达,该船正以16米/秒跨河行驶,水流垂直,因此对河对岸没有影响,行驶所需时间可以通过速度除以速度来确定。

    t = d v = 135   m 16   m/s = 8.4   s
    ::t=dv=135 m16 mm/s=8.4 s

    Example 3
    ::例3

    (c)   The boat is traveling across the river for 8.4 seconds and therefore, it is also traveling downstream for 8.4 seconds.  We can determine the distance downstream the boat will travel by multiplying the speed downstream by the time of the trip.
    :伤心c) 船只横渡河行驶8.4秒,因此,在下游行行驶8.4秒,我们可以确定船只在下游行行驶的距离,在行驶时乘以下游速度。

    d downstream = ( v downstream ) ( t ) = ( 9.0   m/s ) ( 8.4   s ) = 76   m
    ::ddownfream=(vdownf流)(t) =(9.0 m/s)(8.4 s) =76 m

    Use this PLIX Interactive to visualize how any vector can be broken down into separate x and y components:
    ::使用此 PLIX 交互式互动来可视化任何矢量如何分解成独立的 x 和 y 组件 :

    Summary
    ::摘要

    • Vectors can be added mathematically using geometry and trigonometry.
      ::可以通过几何和三角测量数学增加矢量。
    • Vectors that are perpendicular to each other have no effect on each other.
      ::相互垂直的矢量对彼此没有影响。
    • Vector addition can be accomplished by resolving the vectors to be added into components those vectors, and then completing the addition with the perpendiuclar components.
      ::通过解决添加到这些矢量组成部分中的矢量,然后完成添加,并配有perpendiuclar组件,可以实现矢量增加。

    Review
    ::回顾

    1. A hiker walks 11 km due north from camp and then turns and walks 11 km due east.
      1. What is the total distance walked by the hiker?
        ::徒步者走的总距离是多少?
      2. What is the displacement (on a straight line) of the hiker from the camp?
        ::远足者从难民营中流离失所(直线)是什么?

      ::远足者从难民营向北行走11公里,然后向东转转行走11公里。 远足者走的总距离是多少? 远足者从难民营流离失所(直线)是多少?
    2. While flying due east at 33 m/s, an airplane is also being carried due north at 12 m/s by the wind.  What is the plane’s resultant velocity?
      ::当飞机在33米/秒时向东飞行时,风向向北飞行12米/秒。 飞机的飞行速度如何?
    3. Two students push a heavy crate across the floor.  John pushes with a force of 185 N due east and Joan pushes with a force of 165 N at 30° north of east.  What is the resultant force on the crate?
      ::两个学生把一个重箱推过地板。约翰推了185N正向东,琼推了165N,东北30度。
    4. An airplane flying due north at 90. km/h is being blown due west at 50. km/h.  What is the resultant velocity of the plane?
      ::一架在90公里/小时向北飞行的飞机正以50公里/小时向西飞行。

    Explore More
    ::探索更多

    Use this resource to answer the questions that follow.
    ::使用此资源回答下面的问题 。

    1. What are the steps the teacher undertakes in order to calculate the resultant vector in this problem?
      ::教师采取了什么步骤来计算这一问题中由此产生的矢量?
    2. How does she find the components of the individual vectors?
      ::她如何找到单个矢量的成分?
    3. How does she use the individual vector’s components to find the components of the resultant vector?
      ::她如何使用单个矢量的部件来找到由此而来的矢量的部件?
    4. Once the components are determined, how does she find the overall resultant vector?
      ::一旦确定各组成部分,她如何找到由此产生的总体矢量?