节: 线条的其他形式的公式(点式和一般格式) | 3.6 其他形式的线条等式(点-线形形式和一般形式)

章节大纲

You work at a movie theater. For a movie blockbuster, the theater makes $11,850. If adult tickets cost $11 and child tickets cost $6.50, how many child's tickets were sold if they sold 900 adult tickets? In this section, we consider two other forms of the equation of a line to model situations like this one.

Point-Slope Form of the Equation of a Line
::线线的平方

In the previous section, we discussed how to find equations of lines in slope-intercept form . However, sometimes you do not know the y- intercept . There is another form of a line that eliminates the need to know or to find the y- intercept. This is point- form.
::在前一节中,我们讨论了如何在斜坡界面中找到线的方程式。但是, 有时您不知道 y 界面。有另一种形式的线条可以消除知道或找到 y 界面的需要。这是点形式。

As the name implies, point-slope form requires the slope and a point on the line. The equation is essentially a rearrangement of the slope formula . If we take the slope formula and multiply both sides by $\begin{aligned} x_{2} - x_{1} \end{aligned}$ , we get
::正如名称所暗示的,点斜体形式需要斜度和线上的一个点。方程基本上是斜度公式的重新排列。如果我们采用斜度公式,将两边乘以 x2 - x1,我们得到

$\begin{aligned} m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} ⟹ (x_{2} - x_{1}) \cdot m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot (x_{2} - x_{1}) ⟹ m (x_{2} - x_{1}) = y_{2} - y_{1} \end{aligned}$

::my2-y1x2- x1 (x2- x1)\\ m=y2-y1x2- x1)\ x1}(x2- x1)\\ m(x2- x1)=y2-y1

For a fixed m, there are an infinite number of points that satisfy this equation if we know one of the points $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ . To represent this, we replace $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ with variables $\begin{aligned} (x, y) \end{aligned}$ .
::对于一个固定米,如果我们知道一个点(x1,y1),有无限数量的点可以满足这个方程。要代表这个点,我们用变量(x,y)取代(x2,y2),以变量(x,y)取代(x,y)。

Point-Slope Form of the Equation of a Line
::线线的平方

The point-slope form of a line is
::线条的点斜体形式是

$\begin{aligned} y - y_{1} = m (x - x_{1}) \end{aligned}$

::yy1=m(x-x1)

where $\begin{aligned} m \end{aligned}$ is the slope of the line and $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ is a point on the line.
::m 是线的斜坡, (x1,y1) 是线上的一个点。

Example 1
::例1

Find the equation of a line whose slope is 4 and goes through the point (1,3).
::查找斜度为 4 并经过点(1,3) 的线的方程。

Solution: Here we are given the slope and a point on the line, so we use point-slope form. We identify the values for $\begin{aligned} m, x_{1} \end{aligned}$ and $\begin{aligned} y_{1} \end{aligned}$ and substitute into the equation.
::解答: 这里我们给定了斜坡和线上的一个点, 所以我们使用点窗体。我们确定 m、 x1 和 y1 的值, 并替换为等式。

$\begin{aligned} m & = 4 \\ x_{1} & = 1 \\ y_{1} & = 3 \\ y - 3 & = 4 (x - 1) \end{aligned}$
That is the equation of the line with the given properties.
::m= 4x1= 1y1= 3y- 3= 4(x- 1) 这是与给定属性对应的直线方程式。

Example 2
::例2

Find the equation of a line whose slope is $\begin{aligned} \frac{1}{2} \end{aligned}$ and goes through the point (-5,6).
::查找斜坡为12且经过点( 5, 6) 的线的方程。

Solution: Again, we know the slope and a point on the line, so we use point-slope form. Identifying the missing values and substituting into the equation, we have
::解决方案:再次,我们知道斜坡和线上的一个点, 所以我们使用点- 斜坡形式。识别缺失的值, 并替换到方程中, 我们找到了

$\begin{aligned} m & = \frac{1}{2} \\ x_{1} & = - 5 \\ y_{1} & = 6 \\ y - y_{1} & = m (x - x_{1}) \\ y - 6 & = \frac{1}{2} (x - (- 5)) \\ y - 6 & = \frac{1}{2} (x + 5) \end{aligned}$

::m=12x15y1=6y-y1=m(x-x1)-6=12(x-(5))y-6=12(x+5)

Subtracting -5 is the same as addition by 5: keep the sign of the $\begin{aligned} x \end{aligned}$ , change the operation to addition, and change the sign of the second number from negative to positive.
::减法 - 5与增加5:保持x的标记,将操作改为增加,将第二个数字的标记从负数改为正数。

Example 3
::例3

Find the equation of the line that has a slope of -9 and goes through (-7,0).
::查找线的方程,线的斜度为 -9,然后通过(-7,0)。

Solution: Be careful here. The point we have is not the y- intercept. For the y- intercept, the x- value is 0. This is the x- intercept. Using point-slope form, we have
::解答: 注意这里。我们的点不是 y 界面。对于 y 界面, x 值为 0。这是 x 界面。使用 point- slope 格式, 我们已经有了

$\begin{aligned} m & = - 9 \\ x_{1} & = - 7 \\ y_{1} & = 0 \\ y - y_{1} & = m (x - x_{1}) \\ y - 0 & = - 9 (x - (- 7)) \\ y & = - 9 (x + 7) \end{aligned}$

::=%9x17y1=0y-y1=m(x-x1)-0_9(x-(-7))y_9(x+7)

If we distribute the -9 to each one of the terms , we have the equation of this line in slope-intercept form: $\begin{aligned} y = - 9 x - 63 \end{aligned}$ .
::如果我们将 -9 分配到每个术语中, 我们就会在斜坡截取形式上使用此线的方程式 : y9x- 63 。

Example 4
::例4

Find the equation of the line that contains the points (-1,3) and (2,-6).
::查找包含点数(-1,3)和点数(2,6)的线的方程。

Solution: We can use point-slope form since we know two points on the line. First, we need to find the slope.
::解决方案:我们可以使用点窗体,因为我们知道线上有两个点。首先,我们需要找到斜坡。

$\begin{aligned} (x_{1}, y_{1}) = (- 1, 3) \\ (x_{2}, y_{2}) = (2, - 6) \\ m & = \frac{- 6 - 3}{2 - (- 1)} = \frac{- 9}{3} = - 3 \end{aligned}$

:x1,y1) = (-1,3) (x2,y2) = (2,-6) m) 6 - 32 - (-1) 93 3

Now, that we know the slope, we can substitute into the point-slope equation using the $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ we defined above.
::现在,我们知道斜坡, 我们可以用上面定义的(x1,y1) 来替代点偏方程。

$\begin{aligned} y - y_{1} & = m (x - x_{1}) \\ y - 3 & = - 3 (x - (- 1)) \\ y - 3 & = - 3 (x + 1) \end{aligned}$
by CK-12 demonstrates how to write the equations of lines given their slope and y -intercept or two of their points.
::y-y1=m(x-x1)-33(x-(-1))-y-33(x-(-1))-y-3_3(x+1) 由 CK-12 演示如何根据线条的坡度和 y- intercept 或两点写线的方程。

General Form of the Equation of a Line
::线条等式的一般形式

We have another way to write the equation of a line. As we will see, it is a convenient form for graphing and modeling situations.
::我们用另一种方式来写一个线的等式。我们可以看到,它是绘制图表和建模的方便形式。

General Form of the Equation of a Line
::线条等式的一般形式

The general form of a line is
::直线的一般形式是

$\begin{aligned} A x + B y = C \end{aligned}$

::Ax+By=C 轴+By=C

where $\begin{aligned} A, B, \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are real numbers .
::其中A、B和C是真实数字。

To get an equation in general form, you often have to start with one of the other forms and convert those to general form. We see this in the next example.
::要以一般形式获得等式, 您往往必须从其它表格之一开始, 并将这些表格转换为一般形式。我们从下一个示例中看到这一点。

Example 5
::例5

Find the equation of a line in general form where the slope is $\begin{aligned} \frac{3}{4} \end{aligned}$ and passes through (4, -1).
::在斜坡为34且通过(4,-1)的直线中,查找以一般形式表示的直线的方程。

Solution: To find the equation in general form, you need to determine what $\begin{aligned} A, B, \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are. Let’s start this example by finding the equation in point-slope form.
::解决方案 : 要找到一般形式的方程式, 您需要确定 A、 B 和 C 是什么。让我们先从点窗体的方程式开始。

$\begin{aligned} y - (- 1) = \frac{3}{4} (x - 4) \\ y + 1 = \frac{3}{4} (x - 4) \end{aligned}$

::y- (- 1) =34(x-4)y+1=34(x-4)

To change this to general form we need to get the x- and y- terms on the same side of the equation and the numbers on the other side.
::要将其变成一般形式, 我们需要将 X 和 Y 术语放在方程的同一侧, 数字放在另一侧。

$\begin{aligned} y + 1 & = \frac{3}{4} (x - 4) \\ y + 1 & = \frac{3}{4} x - 3 \\ - \frac{3}{4} x + y + 1 & = - 3 \\ - \frac{3}{4} x + y & = - 4 \\ - 4 (- \frac{3}{4} x + y) & = - 4 (- 4) \\ 3 x - 16 y & = 16 \end{aligned}$

::y+1=34x-33-3-34x+y+1}3-34x+y_3x_4_4(-34x+y)_4(- 34x+y)_4(- 34x+y)_4(- 4)_4(- 4)3x-16y=16

by CK-12 demonstrates how to convert from slope-intercept form of a linear equation to the general form.
::通过 CK-12 演示如何从线性方程式的斜度间距形式转换为一般形式。

Example 6
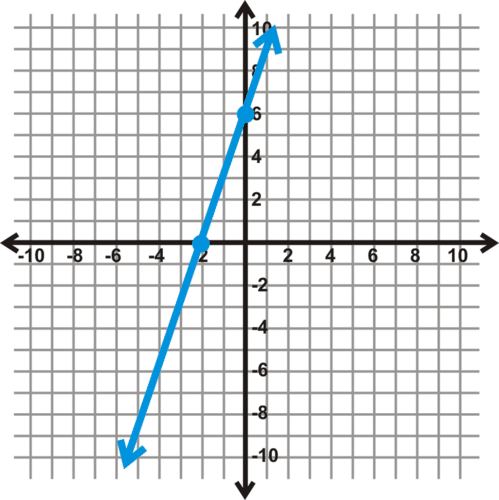
::例6

Find the equation of the line below, in general form.
::查找下面直线的方程式,以一般形式显示。

Solution: Here, we are given the intercepts . Since we have a graph, we can find the slope using rise over run , $\begin{aligned} \frac{6}{2} = 3 \end{aligned}$ and the y- intercept is (0, 6). The equation of the line, in slope-intercept form, is $\begin{aligned} y = 3 x + 6 \end{aligned}$ . To change the equation to general (standard) form, subtract the x- term to move it over to the other side.
::解答 : 在这里, 我们得到拦截。由于我们有一个图表, 我们能找到斜坡, 使用向上移动, 62=3, y 界面是 (0, 6) 。斜坡- 界面形式的线的方程式是 y= 3x+6 。要将方程式更改为一般( 标准) 格式, 请减去 x 期, 将其移到另一侧。

$\begin{aligned} - 3 x + y = 6 \\ - 1 (- 3 x + y) = - 1 (6) OR \\ 3 x - y = - 6 \end{aligned}$

::- 3x+y=6-1(-3x+y)\\\\\\\(6)OR3x-y=6

by CK-12 demonstrates how to write linear equations in general form given two points.
::用 CK-12 演示如何以给定两个点的一般形式写出线性方程式。

Example 7
::例7

You work at a movie theater. For a movie blockbuster, the theater makes $11,850. If adult tickets cost $11 and child tickets cost $6.50, how many child's tickets were sold if they sold 900 adult tickets?
::你在一个电影院工作。对于一个电影大块头来说,电影院赚11 850美元。如果成人票价为11美元,儿童票价为6.50美元,如果他们卖900张儿童票,他们卖了多少张儿童票?

Solution: Let's define some variables. Say $\begin{aligned} a \end{aligned}$ is the number of adult tickets and $\begin{aligned} c \end{aligned}$ is the number of child's tickets. Then, the money made from adult tickets is 11 times the number of adults tickets, or $\begin{aligned} 11 a \end{aligned}$ . Similarly, the amount of money made from child's tickets is $\begin{aligned} 6.5 c \end{aligned}$ . The total amount of money made is
::解决方案:让我们来定义一些变量。说一是成人票数, c是儿童票数。然后, 成人票数是成人票数的11倍, 即11a。同样, 儿童票数的6. 5c。钱总数是6. 5c。

$\begin{aligned} 11 a + 6.5 c = 11, 850 general form \end{aligned}$

::11a+6.5c=11 850一般形式

Since we know the number of adults that purchased tickets, we can find the number of child's tickets by substituting into the equation.
::由于我们知道有多少成年人购买机票,我们可以用方程式来替代儿童机票的数量。

$\begin{aligned} 11 (900) + 6.5 c = 11, 850 \\ 9, 900 + 6.5 c = 11, 850 \\ \underline{- 9, 900 - 9, 900} \\ \frac{6.5 c}{6.5} = \frac{1, 950}{6.5} \\ c = 300 \end{aligned}$

::11(900)+6.5c=11 8509 900+6.5c=11 850-9 900-9 900--9 900-6.5c=1 9506.5c=300

There were 300 child's tickets sold.
::卖了300张孩子的票

by Mathispower4u demonstrates how to write linear equations in general form to represent applications.
::由 Mathispower4u 演示如何以一般形式写成直线方程式以代表应用程序。

Summary
::摘要

Point-slope form ( $\begin{aligned} y - y_{1} = m (x - x_{1}) \end{aligned}$ ): Identify the slope and a point on the line and then substitute for $\begin{aligned} m \end{aligned}$ and $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ .
::点窗体(y-y1=m(x-x1):标明斜坡和线上的一个点,然后取代m和(x1)y1。

General form $\begin{aligned} (A x + B y = C) \end{aligned}$ : Write the equation in slope-intercept or point-slope form and then use inverse operations to get $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ on the same side of the equation and the number on the other side
::一般窗体 (Ax+By=C): 以斜度截面或点窗体形式写入方程,然后使用反向操作获得方形同侧的 x 和 y 和另一侧的数字

Review
::回顾

Find the equation of the lines in point-slope form with the following properties.
::以点倾斜窗体查找线条的方程式,其属性如下。

1. slope = 2 and passes through (3, -5)
::1. 斜坡=2,通过(3,5)

2. slope $\begin{aligned} = - \frac{1}{2} \end{aligned}$ and passes through (6, -3)
::2. 斜度 12 和通过(6, 3)

3. passes through (5, -7) and (-1, 2)
::3. 通过(5,-7)和(1、2)

4. passes through (-5, -5) and (5, -3)
::4. 通过(5-5、5-5)和(5、3)

Find the equation of the lines in general form with the following properties.
::以下列属性查找直线的直线方程式的一般形式。

5. x- intercept = (-4,0) and y- intercept = (0,6)
::5. x 截取 = (4,0)和y 截取 = (0,6)

6. slope = -3 and passes through (2,6)
::6. 坡度=-3和通过(2,6)

7. equation of the line is $\begin{aligned} y = - \frac{2}{3} x + 4 \end{aligned}$
::7. y23x+4是y23x+4

8. equation of the line is $\begin{aligned} y - 8 = 4 (x - 2) \end{aligned}$
::8. Y-8=4(x-2)的直线等式为y-8=4(x-2)

Convert the following equations into slope-intercept form.
::将以下方程式转换为斜坡界面形式。

9. $\begin{aligned} 4 x + 5 y = 20 \end{aligned}$
::9. 4x+5y=20

10. $\begin{aligned} y + 3 = - \frac{3}{2} (x - 8) \end{aligned}$
::10. y+332(x-8)

Explore More
::探索更多

1. a. Find the equation of the line in point-slope form that passes through (-1,5) and (4,0) using (-1,5) as the point on the line.
::1. 将线条的方程以点窗体(1、5)和(4、0)以(1、5)作为线上点。

b. Next, find the equation of the line in point-slope form using (4,0).
::b. 下一步,用点窗体(4,0)找到线的方程式。

c. Convert each line into slope-intercept form. Does the point you choose in point-slope form matter?
::c. 将每条线转换为斜坡界面。用点偏斜窗体选择的点是否重要?

2. a. Change $\begin{aligned} A x + B y = C \end{aligned}$ into slope-intercept form. What are the slope and y- intercept equal to (in terms of $\begin{aligned} A, B, \end{aligned}$ and/or $\begin{aligned} C \end{aligned}$ )?
::2. a. 将Ax+By=C改为斜坡界面。斜坡和Y(A、B和/或C)等于什么?

b. Find one possible combination of $\begin{aligned} A, B, \end{aligned}$ and $\begin{aligned} C \end{aligned}$ for $\begin{aligned} y = \frac{1}{2} x - 4 \end{aligned}$ . Write your answer in general form.
::b. 为y=12x-4寻找A、B和C的可能组合。

3. a. The population of a town gradually decreases by about 50 people a year. In 2010, the population was 8,500 people. Write an equation in general form for the population of this town .
::3.a. 城镇人口每年逐步减少约50人,2010年人口为8,500人,为城镇人口撰写一个通用方程式。

b. At this rate, when will the population of the town be 0 people?
::b. 按此速度计算,该镇人口何时为0人?

4. You are 300 miles from home and driving at a speed of 55 mph. If $\begin{aligned} c h a n g e i n d i s t a n c e = r a t e \cdot c h a n g e i n t i m e \end{aligned}$ , write an equation in point-slope form to model your drive home.
::4. 你离家300英里,驾驶速度55英里,如果时间的距离=率变化改变,用点窗形写一个方程来模拟驾驶车回家。

5. You invest money into two accounts. The first account earns 2% interest and the second 5% interest. If you made a total of $165 in interest and you invested $3,000 in the first account, how much did you invest in the second account?
::5. 你将资金投资于两个账户:第一个账户赚取2%的利息,第二个账户赚取5%的利息;如果总共赚了165美元的利息,并在第一个账户上投资了3 000美元,那么在第二个账户上投资了多少?

by Mathispower4u is a continuation of the previous video and explains how to write a linear equation in general form to represent an application.
::Mathispower4u 是前一段视频的继续, 解释如何写出一般形式的线性方程式, 以代表应用程序。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try these interactives that reinforce the concepts explored in this section:
::尝试这些强化本节所探讨概念的交互作用 :

章节大纲

Point-Slope Form of the Equation of a Line ::线线的平方

Point-Slope Form of the Equation of a Line ::线线的平方

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

General Form of the Equation of a Line ::线条等式的一般形式

General Form of the Equation of a Line ::线条等式的一般形式

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Point-Slope Form of the Equation of a Line
::线线的平方

Point-Slope Form of the Equation of a Line
::线线的平方

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

General Form of the Equation of a Line
::线条等式的一般形式

General Form of the Equation of a Line
::线条等式的一般形式

Example 5
::例5

Example 6
::例6

Example 7
::例7

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX