节: 水平和垂直线 | 3.7 水平线和垂直线

章节大纲

Suppose you are designing a house in a computer design program. You line up walls on horizontal and vertical lines in the grid. How would we describe these walls in the coordinate plane ? We discuss that in this section.

Horizontal Lines
::水平线

To determine an equation for horizontal lines, let's consider an example of a table of values for points on a horizontal line. If we plot these points and draw a line through them, the line will be horizontal.
::要确定水平线的方程, 让我们来考虑一个水平线上的点的数值表格示例。如果我们绘制这些点并通过它们绘制一条线, 该线将是水平的。

$\begin{aligned} \begin{array}{cc} x & y \\ - 3 & 4 \\ 0 & 4 \\ 2 & 4 \end{array} \end{aligned}$

::xy-340424xy-340424

Since we can find the , 0, and we are given the y- intercept (0,4), we can find the equation of the line by using slope-intercept form .
::既然我们能找到,0, 并且我们得到了 Y 界面( 0, 4), 我们就可以通过使用斜坡界面来找到线的方程。

$\begin{aligned} y & = m x + b \\ y & = 0 x + 4 \\ y & = 4 \end{aligned}$

::y=mx+by=0x+4y=4 y=4 y

Notice how this equation makes sense given the values in the table. All of y- values in the table are 4, so they satisfy this equation.
::注意这个方程式在表格中值是否合理。表格中的所有 Y 值都是 4 , 所以它们满足了这个方程式。

Horizontal Lines
::水平线

In general, the equation of a horizontal line is
::一般而言,横向线的方程式是

$\begin{aligned} y = c \end{aligned}$
where $\begin{aligned} c \end{aligned}$ is a real number .
::y=c,C是一个真实的数字。

Example 1
::例1

Find the equation of the the line that goes through (-2,-2) and (1,-2) and graph it.
::查找通过线( 2-2) 和(1, 2) 的方程式, 并绘制图表。

Solution: These points share a common y- value, so the slope of the line that contains these points is 0. It is a horizontal line. Its equation is $\begin{aligned} y = - 2 \end{aligned}$ .
::解决方案 : 这些点有一个共同的 Y 值, 因此包含这些点的线的斜度是 0。这是一个水平线。它的方程是 y 2 。

To graph it, we plot the two points and draw a horizontal line through them.
::为了绘制图表,我们绘制两点,并绘制一条横线。

Example 2
::例2

Find the equation of the horizontal line through (-4, 1) and graph it.
::查找横线( 4, 1) 的方程式, 并绘制图表。

Solution: This point needs to satisfy the equation, so we use its $\begin{aligned} y \end{aligned}$ -value. The equation of the line is $\begin{aligned} y = 1 \end{aligned}$ . To graph the line, plot the point (-4, 1) and draw a horizontal line through it.
::解答 : 此点需要满足方程式, 所以我们使用它的 Y 值。线的方程式是 y= 1 。要绘制线条图, 绘制点( 4 、 1) 并通过它绘制水平线。

by CK-12 demonstrates how to determine if a line is vertical or horizontal given the equation of the line.
::通过 CK-12 演示如何根据线的方程确定一条线是垂直线还是水平线。

Vertical Lines
::垂直直线

We can approach our search for an equation for vertical lines in a similar way to horizontal lines.
::我们可以以与水平线相似的方式寻找垂直线的方程式。

To determine a general equation for vertical lines, let's consider a table of values for points on a vertical line. For example,
::要确定垂直线的一般方程, 我们考虑垂直线上的点的数值表。例如,

$\begin{aligned} \begin{array}{cc} x & y \\ 3 & - 2 \\ 3 & 1 \\ 3 & 5 \end{array} \end{aligned}$

::xy3-23135xy3-23135

We cannot use any of the forms of the equation of a line since the slope is undefined . However, notice that all of the x- values are the same. An equation that would satisfy all of these points would be $\begin{aligned} x = 3 \end{aligned}$ .
::由于斜坡没有定义, 我们不能使用线形方程的任何形式。但是, 请注意所有 x 值都是相同的。满足所有这些点的方程是 x= 3 。

Vertical Lines
::垂直直线

In general, the equation of a vertical line is
::一般而言,纵向线的等式是:

$\begin{aligned} x = c \end{aligned}$
where $\begin{aligned} c \end{aligned}$ is a real number.
::x=c,其中c是一个真实数字。

Example 3
::例3

Find the equation of the the line that goes through (-1,2) and (-1,5) and graph it.
::查找通过线( 1, 2) 和( 1, 5) 的方程式, 并绘制图表。

Solution: These points share an x- value, so the slope of the line that contains these points is undefined. It is a vertical line. Its equation is $\begin{aligned} x = - 1 \end{aligned}$ .
::解析度 : 这些点共享 x 值, 因此包含这些点的线条的斜度是未定义的。它是一个垂直线。它的方程式是 x\\\ 1 。

To graph it, we plot the two points and draw a vertical line through them.
::为了绘制图表,我们绘制两点图,并划一条垂直线通过这两点。

Example 4
::例4

Find the equation of the vertical line through (2,3) and graph it.
::查找垂直线通过(2,3)的方程式并绘制图表。

Solution: This point needs to satisfy the equation, so we use its x- value. The equation of the line is $\begin{aligned} x = 2 \end{aligned}$ .
::解答 : 此点需要满足方程式, 所以我们使用它的 X 值。线的方程式是 x= 2 。

To graph the line, plot the point (2,3) and draw a vertical line through it.
::要绘制线条图, 绘制点( 2, 3) 并通过它绘制一条垂直线。

by CK-12 is a continuation of the previous video and demonstrates how to determine if a line is vertical or horizontal given the equation of the line.
::CK-12是前一段视频的延续,并显示如何根据线的方程确定一条线是垂直线还是水平线。

Example 5
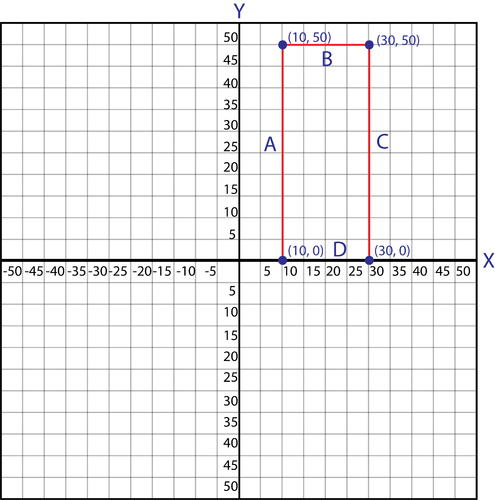
::例5

Find the equations of the lines that contain the line segments for the walls below.
::查找包含以下墙壁线段的线条方程式的方程式。

Solution:
::解决方案 :

Line Segment A: The points on line segment A share an x- value of 10. The equation of the line that contains this line segment is $\begin{aligned} x = 10 \end{aligned}$ .
::线段A:线段A的点的X值为10。包含此线段的线的方程式是x=10。

Line Segment B: The points on line segment B share a y- value of 50. The equation of the line that contains this line segment is $\begin{aligned} y = 50 \end{aligned}$ .
::线段B:线段B的点的Y值为50,包含该线段的线的方程式为y=50。

Line Segment C: The points on line segment C share an x- value of 30. The equation of the line that contains this line segment is $\begin{aligned} x = 30 \end{aligned}$ .
::C线段:C线段上的点数的X值为30,包含该线段的线的方程式为x=30。

Line Segment D: The points on line segment D share an y- value of 0. The equation of the line that contains this line segment is $\begin{aligned} y = 0 \end{aligned}$ .
::线段 D : 线段 D 上的点值为 0 y。包含此线段的线的方程式是 y= 0 。

by Randy Anderson explains the connection between the equations, graphs, and slopes of vertical and horizontal lines.
::Randy Anderson解释了垂直和水平线的方程式、图表和斜坡之间的联系。

Summary
::摘要

Horizontal lines have zero slope and their equations are of the form $\begin{aligned} y = c \end{aligned}$ .
::水平线为零斜度,其方程式为y=c。

Vertical lines have undefined slope and their equations are of the form $\begin{aligned} x = c \end{aligned}$ .
::垂直线有未定义的斜坡,其方程式为表x=c。

Review
::回顾

Find the equation of the lines with the given properties.
::根据给定属性查找线条的方程。

1. slope = 0 and passes through (-4,3)
::1. 斜坡=0,通过(4-3)

2. slope is undefined and passes through (-2.-5)
::2. 坡度未定义,通过(-2.5)

3. passes through (1,4) and (1,8)
::3. 通过(1,4)和(1,8)

4. passes through (3,5) and (7,5)
::4. 通过(3,5)和(7,5)

5. passes through (-6,12) and (-6,18)
::5. 通过(-6,12)和(-6,18)

6. passes through (0,-7) and (-7,-7)
::6. 通过(0、7)和(7、7)

Graph the following lines.
::绘制下行图。

7. $\begin{aligned} y = 4 \end{aligned}$
::7.y=4

8. $\begin{aligned} x = 1 \end{aligned}$
::8. x=1

9. $\begin{aligned} y = - 2 \end{aligned}$
::9. y2

10. $\begin{aligned} x = - 3 \end{aligned}$
::10. 3x%3

Explore More
::探索更多

1. The x- and y- axes are horizontal and vertical lines. What are the equations of the lines that describe the points on the x- and y- axes, respectively?
::1. x 轴和 y 轴是水平线和垂直线。描述 x 轴和 y 轴两点的线的方程式是什么?

2. Suppose you are at an all-you-can-eat pancake house where you can pay $8.99 and have all the pancakes you want. What if you graphed the number of pancakes you ate along the x- axis and the amount of money you have to pay along the y- axis. Would the line representing this situation be horizontal or vertical? Write the equation of the line that represents this situation.
::2. 假设你住在一个全能的煎饼房里,在那里你可以支付8.99美元,并拥有所有你想要的煎饼。如果你用图表显示你沿着x轴吃了多少煎饼,以及你必须沿着y轴支付多少钱。代表这种情况的线是水平的还是垂直的?写出代表这种情况的线的等式。

3. Mad Cabs have an unusual offer going on. They are charging $7.50 for a taxi ride of any length within the city limits. Graph the function that relates the cost of hiring the taxi ( $\begin{aligned} y \end{aligned}$ ) to the length of the journey in miles ( $\begin{aligned} x \end{aligned}$ ). Write the equation of the line that represents this situation.
::3. 疯狂出租车有不寻常的报价,在城市界限内乘坐任何长度的出租车要收费7.50美元,将雇用出租车的费用与行程的里程(x)有关。写出反映这种情况的线的方程。

by CK-12 shows an example similar to problem 3.
::CK-12 显示一个类似于问题3的例子。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.

::请参看附录。

PLIX
::PLIX

Try this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:

章节大纲

Horizontal Lines ::水平线

Horizontal Lines ::水平线

Example 1 ::例1

Example 2 ::例2

Vertical Lines ::垂直直线

Vertical Lines ::垂直直线

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Horizontal Lines
::水平线

Horizontal Lines
::水平线

Example 1
::例1

Example 2
::例2

Vertical Lines
::垂直直线

Vertical Lines
::垂直直线

Example 3
::例3

Example 4
::例4

Example 5
::例5

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX