Section: 以替代方式解决等式的解决系统 | 4.4 用替代方式解决等式的溶解系统

Section outline

Rex and Carl are making a mixture in science class. They need to have 12 ounces of a 60% saline solution. To make this solution they have a 20% saline solution and an 80% saline solution. How many ounces of each do they need to make the correct mixture?
::Rex和Carl正在科学类中制造混合体。他们需要12盎司的60%盐碱溶液。要让这个溶液达到20%的盐碱溶液和80%的盐碱溶液。每种溶液需要多少盎司才能做出正确的混合?

In this section, we will discuss how to solve a system like this algebraically.
::在本节中,我们将讨论如何解决这样一个代数系统。

lesson content

Solving a System of Equations by Substitution
::以替代方式解决分配制度

In the substitution method, we will be looking at the two equations and deciding which variable is easiest to solve for so that we can write one of the equations as $\begin{aligned} x = \end{aligned}$ or $\begin{aligned} y = \end{aligned}$ . Next we will replace either the $\begin{aligned} x \end{aligned}$ or the $\begin{aligned} y \end{aligned}$ accordingly in the other equation . The result will be an equation with only one unknown that we can solve. It is helpful to isolate a variable whose coefficient is 1 or -1.
::在替代方法中,我们将查看这两个方程,并决定最容易解决的变量,以便我们可以将其中一个方程写入 x= 或 Y= 。接下来,我们将在另一个方程中相应替换 x 或 y。结果将是一个方程,只有一个未知的方程,我们可以解开。将系数为 1 或 - 1 的变量分离出来是有益的。

Example 1
::例1

Solve the system using substitution:
::使用替代解决系统:

\begin{aligned} 2 x + y & = 12 \\ - 3 x - 5 y & = - 11 \end{aligned}

::2x+y=12-3x-5y11

Solution: The first step is to look for a variable that is easy to isolate. In other words, does one of the variables have a coefficient of 1. Yes, that variable is the $\begin{aligned} y \end{aligned}$ in the first equation. So, start by isolating or solving for $\begin{aligned} y \end{aligned}$ : $\begin{aligned} y = - 2 x + 12. \end{aligned}$
::解决方案: 第一步是寻找一个容易分离的变量。换句话说, 变量之一的系数是否为 1 。是的, 该变量是第一个方程式中的 y 。因此, 从孤立或解决 y: y&2x+12 开始。

This expression can be used to replace the $\begin{aligned} y \end{aligned}$ in the other equation and solve for $\begin{aligned} x \end{aligned}$ :
::此表达式可用于替换其他方程式中的 Y, 并解决 x:

\begin{aligned} - 3 x - 5 (- 2 x + 12) & = - 11 \\ - 3 x + 10 x - 60 & = - 11 \\ 7 x - 60 & = - 11 \\ 7 x & = 49 \\ x & = 7 \end{aligned}

::-3x-5(- 2x+12) 11- 3x+10x- 60) 117x- 60 *117x=117x=49x=7

Now that we have found $\begin{aligned} x \end{aligned}$ , we can use this value in our expression to find $\begin{aligned} y \end{aligned}$ :
::既然我们找到了 x, 我们可以在表达式中使用这个值来查找 y:

\begin{aligned} y & = - 2 (7) + 12 \\ y & = - 14 + 12 \\ y & = - 2 \end{aligned}

::y2(7)+12y14+12y2

Recall that the solution to a linear system is a point in the coordinate plane where the two lines intersect. Therefore , our solution should be written as a point: (7, -2). We can check the solution by substituting this point into both equations to make sure that it satisfies them:
::回顾线性系统的解决方案是坐标平面上两条线交叉的一个点。因此,我们的解决办法应该写成一个点 : (7, - 2) , 我们可以用两个方程式来取代这个点来检查解决方案, 以确保它满足这两个方程式 :

\begin{aligned} 2 (7) + - 2 & = 14 - 2 = 12 \\ - 3 (7) - 5 (- 2) & = - 21 + 10 = - 11 \end{aligned}

by CK-12 demonstrates how to solve a system of equations by substitution .
::通过 CK-12 演示如何通过替代解决方程式系统。

Example 2
::例2

Solve the system using substitution:
::使用替代解决系统:

\begin{aligned} 2 x + 3 y & = 13 \\ x + 5 y & = - 4 \end{aligned}

::2x+3y=13x+5y4

Solution: In the last example, $\begin{aligned} y \end{aligned}$ was the easiest variable to isolate. This time $\begin{aligned} x \end{aligned}$ is the variable with a coefficient of 1. Solving the second equation for $\begin{aligned} x \end{aligned}$ gives: $\begin{aligned} x = - 5 y - 4 \end{aligned}$ .
::解答 : 在最后一个示例中, y 是最容易分离的变量。此时 x 是系数为 1 的变量。解答 x 的第二个方程式 : x5y-4 。

This expression can be used to replace the $\begin{aligned} x \end{aligned}$ in the other equation and solve for $\begin{aligned} y \end{aligned}$ :
::此表达式可用于替换其他方程式中的 x, 并解决 y:

\begin{aligned} 2 (- 5 y - 4) + 3 y & = 13 \\ - 10 y - 8 + 3 y & = 13 \\ - 7 y - 8 & = 13 \\ - 7 y & = 21 \\ y & = - 3 \end{aligned}

::2(-5y-4)+3y=13-10y-8+3y=13-7y-8=13-7y-8=13-7y=21y3

Now that we have found $\begin{aligned} y \end{aligned}$ , we can use this value in our expression to find $\begin{aligned} x \end{aligned}$ :
::既然我们找到了y, 我们可以在表达式中使用这个值来找到x:

\begin{aligned} x & = - 5 (- 3) - 4 \\ x & = 15 - 4 \\ x & = 11 \end{aligned}

::x5(- 3) - 4x=15 - 4x=11

So, the solution to this system is (11, -3). Do not forget to check the solution :
::因此,这个系统的解决方案是 (11, - 3) , 不要忘了检查解决方案 :

\begin{aligned} 2 (11) + 3 (- 3) & = 22 - 9 = 13 \\ 11 + 5 (- 3) & = 11 - 15 = - 4 \end{aligned}

Example 3
::例3

Solution:

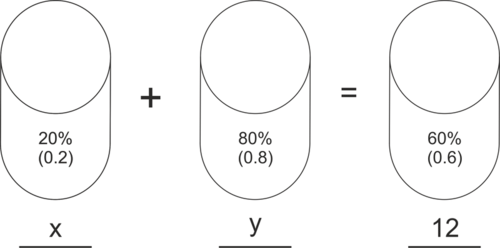
::解决方案 :

Let’s organize our information in a picture as shown below:
::让我们将我们的信息整理成如下图示:

lesson content

In this picture, we can see that we will be mixing $\begin{aligned} x \end{aligned}$ ounces of the 20% solution with $\begin{aligned} y \end{aligned}$ ounces of the 80% solution to get 12 ounces of the 60% solution. We could also organize the information in a table as follows:
::在这张图中,我们可以看到,我们将把20%的溶液的x盎司与80%的溶液的y盎司混合,以获得60%的溶液的12盎司。

	ounces liquid	% saline	total ounces saline
20% solution ::解决方案	x	0.20	0.20x
80% solution ::解决方案	y	0.80	0.80y
60% solution ::解决方案	12	0.60	0.60(12)

The two equations are thus:
::因此,两个方程式是:

\begin{aligned} 0.2 x + 0.8 y & = 0.6 (12) \\ x + y & = 12 \end{aligned}

::0.2x+0.8.8y=0.6(12)x+y=12

Now we can solve the system using substitution. Solve for $\begin{aligned} y \end{aligned}$ in the second equation to get: $\begin{aligned} y = 12 - x \end{aligned}$ .
::现在我们可以用替换解决系统。在第二个方程式中为 y 解决 y , 获得 y= 12 - x 。

Now, substitute in and solve the first equation:
::现在,用第一个方程式来替代和解决第一个方程式:

\begin{aligned} 0.2 x + 0.8 (12 - x) & = 0.6 (12) \\ 0.2 x + 9.6 - 0.8 x & = 7.2 \\ - 0.6 x & = - 2.4 \\ x & = 4 \end{aligned}

::0ux+0.8(12-x)=0.6(12)0.0.2x+9.6-0.8x=7.2-0.6x=0.6x2.4x=4

Now we can find $\begin{aligned} y \end{aligned}$ :
::现在我们可以找到y:

\begin{aligned} y & = 12 - x \\ y & = 12 - 4 \\ y & = 8 \end{aligned}

::y=12-xy=12-4y=8

Therefore, Rex and Carl need 4 ounces of the 20% saline solution and 8 ounces of the 80% saline solution to make the correct mixture.
::因此,Rex和Carl需要 20%盐碱溶液的4盎司 80%盐溶液的8盎司才能做出正确的混合物

Example 4
::例4

Solve the following system of equations:

\begin{aligned} y & = \frac{1}{2} x - 21 \\ y & = - 2 x + 9 \end{aligned}

::解决以下方程式系统: y= 12x- 21y= @% 2x+9

Solution: In this case, both equations are equal to $\begin{aligned} y \end{aligned}$ . Since $\begin{aligned} y = y \end{aligned}$ , we can let the right hand sides of the equations be equal too. This is still a substitution problem; it just looks a little different.
::解决方案 : 在此情况下, 两个方程式都等于y。因为y=y, 我们可以让方程式的右侧也相等。这仍然是一个替代问题; 它看起来有点不同。

\begin{aligned} \frac{1}{2} x - 21 & = - 2 x + 9 \\ 2 (\frac{1}{2} x - 21 & = - 2 x + 9) \\ x - 42 & = - 4 x + 18 \\ 5 x & = 60 \\ x & = 12 \end{aligned}

::12 - 212x+92( 12x - 212x+9) x - 424x+185x=60x=12

Now we can find $\begin{aligned} y \end{aligned}$ :
::现在我们可以找到y:

\begin{aligned} y & = \frac{1}{2} (12) - 21 y = - 2 (12) + 9 \\ y & = 6 - 21 o r y = - 24 + 9 \\ y & = - 15 y = - 15 \end{aligned}

::y=12( 12)- 21y @ 2( 12)+9y=6- 21ory @ 24+9_ 15y}15

Therefore our solution is (12, -15).
::因此,我们的解决办法是(12,15)。

Now that we have solved some systems of equations by substitution, let's summarize the process into some steps.
::既然我们已经通过替代解决了一些方程式系统, 让我们把过程总结为一些步骤。

Solving a System of Equations by Substitution
::以替代方式解决分配制度

1. Choose a variable to isolate in one of the equations. A variable with a coefficient of 1 or -1 is a good choice.
::1. 选择一个变量,在其中一个方程中分离。一个系数为1或-1的变量是一个很好的选择。

2. Isolate that variable in the equation and then substitute into the other equation to solve for the variable you did not choose.
::2. 在方程中分离该变量,然后换成另一个方程,以解决您没有选择的变量。

3. Substitute the known value into either equation to find the missing value.
::3. 将已知值替换成任一方程以寻找缺失值。

When a system has no solution or an infinite number of solutions and we attempt to find a single, unique solution using an algebraic method, such as substitution, the variables will cancel out and we will have an equation consisting of only constants. If the equation is false as seen below in Example 5, then the system has no solution. If the equation is always true, as seen in Example 6, then there are infinitely many solutions.
::当一个系统没有解决方案或无限数的解决方案,而我们试图用代数法(如替代)找到一个单一的独特解决方案时,变量就会取消,我们就会有一个由常数组成的方程式。如果公式是假的,如下面例5所示,那么这个系统就没有解决方案。如果方程式总是真实的,如例6所示,那么就有很多解决方案。

Example 5
::例5

Solve the system using substitution:
::使用替代解决系统:

\begin{aligned} 3 x - 2 y & = 7 \\ y & = \frac{3}{2} x + 5 \end{aligned}

::3x-2yy=7y=32x+5

Solution: Since the second equation is already solved for $\begin{aligned} y \end{aligned}$ , we can use this in the first equation to solve for $\begin{aligned} x \end{aligned}$ :
::解答: 由于y的第二个方程式已经解答, 我们可以在第一个方程式中用这个解答 x:

\begin{aligned} 3 x - 2 (\frac{3}{2} x + 5) & = 7 \\ 3 x - 3 x + 5 & = 7 \\ 5 & \neq 7 \end{aligned}

::3x-2(32x+5)=73x-3x+5=757

Since the substitution above resulted in the elimination of the variable, $\begin{aligned} x \end{aligned}$ , and a false equation involving only constants, the system has no solution. The lines are parallel and the system is inconsistent .
::由于上述替换导致变数、x和只涉及常数的虚假方程式被删除,该系统没有解决办法,线条平行,系统不一致。

by Mathispower4u demonstrates how to solve a system of equation using the substitution method. This example has no solutions.
::由 Mathispower4u 演示如何使用替代方法解析方程式系统。此示例没有解决方案。

Example 6
::例6

Solve the system using substitution:
::使用替代解决系统:

\begin{aligned} - 2 x + 5 y & = - 2 \\ 4 x - 10 y & = 4 \end{aligned}

::- 2x+5y24x-10y=4

Solution: We can solve for $\begin{aligned} x \end{aligned}$ in the first equation as follows:
::解答: 我们可以解答第一个方程式中的 x 如下:

\begin{aligned} - 2 x & = - 5 y - 2 \\ x & = \frac{5}{2} y + 1 \end{aligned}

::-2x=52y+1 -2x=52y+1

Now, substitute this expression into the second equation and solve for $\begin{aligned} y \end{aligned}$ :
::现在,将此表达式替换为第二个方程, 并解决 y:

\begin{aligned} 4 (\frac{5}{2} y + 1) - 10 y & = 4 \\ 10 y + 4 - 10 y & = 4 \\ 4 & = 4 \\ (0 & = 0) \end{aligned}

::4(52y+1)-10y=410y+4-10y=44=4(0=0)

In the process of solving for $\begin{aligned} y \end{aligned}$ , the variable is cancelled out and we are left with only constants. We can stop at the step where 4 = 4 or continue and subtract 4 on each side to get 0 = 0. Either way, this is a true statement. As a result, we can conclude that this system has an infinite number of solutions. The lines are coincident and the system is consistent and dependent .
::在解决 y 的过程中, 变量被取消, 我们只剩下常数。我们可以停留在 4 = 4 或 4 = 4 或继续, 然后在每侧减 4 以获得 0 = 0 = 0 的阶梯上。无论如何, 这是一个真实的语句。因此, 我们可以得出这样的结论: 这个系统有无限数量的解决方案。线条是同步的, 系统是一致和依赖的。

by Mathispower4u demonstrates how to solve a system of linear equations using the substitution method. The example has an infinite number of solutions.
::通过 Mathispower4u 演示如何使用替代方法解决线性方程式系统。示例有无限数量的解决方案。

Feature: Clean That Scrape, But Don't Get Burned
::特写: 清除那破烂, 但不要被烧伤

by Kathy Kehrli
::作者:凯西·凯勒利

Have you ever fallen off your bike and scraped your knee? Perhaps you cleaned that scrape with hydrogen peroxide. But did you know that not all bottles of hydrogen peroxide have the same concentration of hydrogen peroxide?
::你曾经从自行车上摔下来并刮过膝盖吗?也许你用过氧化氢清洗过氧化氢的刮痕。但你知道,并非所有的过氧化氢瓶都具有同样的过氧化氢浓度吗?

In fact, high concentrations of hydrogen peroxide (30% or higher) are used as a component of rocket fuels and can burn the skin. What’s more, the Agency for Toxic Substances and Disease Registry warns that breathing in the vapors of even a 10% solution of hydrogen peroxide may result in severe lung irritation. You certainly do not want to trade a scrape for something far worse.
::事实上,高浓度的过氧化氢(30%或更高)被用作火箭燃料的一部分,可以燃烧皮肤。此外,有毒物质和疾病登记署警告说,即使氢过氧化物的10%溶液在蒸气中呼吸也可能导致严重的肺刺激。您当然不想用刮痕换取更糟糕的东西。

The hydrogen peroxide that you find in your local drugstore, like the bottle above, is typically a 3% solution. Food Grade hydrogen peroxide, used in the production of foods like cheese and eggs usually comes in a 35% solution. A 90% concentration solution of hydrogen peroxide is actually used as an oxygen source for rocket fuel! Chemists can combine solutions of various concentrations to produce a hydrogen peroxide solution that has the concentration that they are aiming for. For example, teeth whitening strips typically contain 14% hydrogen peroxide.
::在本地药店中发现的氢过氧化物,就像上面的瓶子一样,通常是一种3%的溶液。食品级过氧化氢,用于生产奶酪和鸡蛋等食品,通常有35%的溶液。过氧化氢90%的浓度溶液实际上被用作火箭燃料的氧源。化学家可以将各种浓度的溶液结合起来,产生一种具有其目标浓度的过氧化氢溶液。例如,牙齿白条通常含有14%的过氧化氢。

by Canada Science and Technology Museum uses experiments to demonstrate the difference between an endothermic reaction and an exothermic reaction. The scientist uses hydrogen peroxide in one of the experiments.
::加拿大科学和技术博物馆利用实验来证明内温反应和异温反应之间的区别。科学家在其中一项实验中使用过氧化氢。

Summary
::摘要

To solve a system of equations by substitution, isolate a variable in one of the equations and substitute into the other equation to find a value. Then, substitute the value into either equation.
::要通过替代解决方程式系统,在其中一个方程式中分离一个变量,并替换到另一个方程式中以找到一个值。然后,将数值替换成两个方程式中任何一个。

Review
::回顾

Solve the following systems using substitution.
::使用替代方法解决以下系统。

\begin{aligned} \begin{aligned} x + 3 y & = - 1 \\ 2 x + 9 y & = 7 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 7 x + y & = 6 \\ x - 2 y & = - 12 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 5 x + 2 y = 0 \\ y = x - 7 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 2 x - 5 y = 21 \\ x = - 6 y + 2 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} y = x + 3 \\ y = 2 x - 1 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} x + 6 y = 1 \\ - 2 x - 11 y = - 4 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 2 x + y = 18 \\ - 3 x + 11 y = - 27 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 2 x + 3 y & = 5 \\ 5 x + 7 y & = 8 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} - 7 x + 2 y & = 9 \\ 5 x - 3 y & = 3 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 2 x - 6 y = - 16 \\ - 6 x + 10 y = 8 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 2 x - 3 y & = - 3 \\ 8 x + 6 y & = 12 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 17 x - 3 y = 5 \\ y = 3 x + 1 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} 4 x - 14 y = 21 \\ y = \frac{2}{7} x + 7 \end{aligned} \end{aligned}

\begin{aligned} \begin{aligned} - 24 x + 9 y & = 12 \\ 8 x - 3 y & = - 4 \end{aligned} \end{aligned}

Explore More
::探索更多

1. Alicia and Sarah are at the supermarket. Alicia wants to get peanuts from the bulk food bins and Sarah wants to get almonds. The almonds cost $6.50 per pound and the peanuts cost $3.50 per pound. Together they buy 1.5 pounds of nuts. If the total cost is $6.75, how much did each girl get? Set up a system to solve using substitution.
::1. Alicia和Sarah在超市,Alicia想从散装食品箱里买花生,Sarah想买杏仁,杏仁每磅6.50美元,花生每磅3.50美元,他们一起购买1.5磅坚果,如果总成本是6.75美元,每个女孩能得到多少?建立一个系统,用替代方法解决。

2. Marcus goes to the department store to buy some new clothes. He sees a sale on t-shirts ($5.25) and shorts ($7.50). Marcus buys seven items and his total, before sales tax, is $43.50. How many of each item did he buy?
::2. Marcus去百货商店买一些新衣服,他看到一件T恤(5.25美元)和短裤(7.50美元)的销售;Marcus买七件,在销售税之前,他的总额是43.50美元。

3. Jillian is selling tickets for the school play. Student tickets are $3 and adult tickets are $5. If 830 people buy tickets and the total revenue is $3,104, how many students attended the play?
::3. Jillian出售学校游戏的票,学生票为3美元,成人票为5美元,如果830人买票,总收入为3 104美元,有多少学生参加了比赛?

4. Paran's cell phone company charges a flat rate of $25 per month plus $0.25 per text. Marcel's cell phone company charges a flat rate of $100 and $1 per text. Marcel's bill for the month is four times Paran's. If they sent the same number of texts, how many did they each send?
::4. 帕拉恩的手机公司每月收费25美元,每文本0.25美元,每文本0.25美元;马塞尔的手机公司收费100美元,每文本1美元;马塞尔的每月账单是帕拉的4倍;如果他们发送相同数量的文本,他们每人发送多少份?

5. A chemist has two containers, Mixture A and Mixture B. Mixture A has a 60% copper sulfate concentration. Mixture B has a 5% copper sulfate concentration. The chemist needs to have a mixture equaling 500 mL with a 15% concentration. How much of each mixture does the chemist need?
::5. 化学家有两个容器,即混合物A和混合物B。混合物A的铜硫酸盐浓度为60%,混合物B的铜硫酸盐浓度为5%,化学家需要的混合物等于500毫升,浓度为15%。每种混合物需要多少?

6. A coffee company makes a product which is a mixture of two coffees, using a coffee that costs $10.20 per pound and another coffee that costs $6.80 per pound. In order to make 20 pounds of a mixture that costs $8.50 per pound, how much of each type of coffee should it use?

::6. 咖啡公司生产一种由两杯咖啡混合而成的产品,它使用每磅10.20美元的咖啡和每磅6.80美元的咖啡,为了制造每磅8.50美元的20磅混合物,每种咖啡应使用多少?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:

Section outline

Solving a System of Equations by Substitution ::以替代方式解决分配制度

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Solving a System of Equations by Substitution ::以替代方式解决分配制度

Example 5 ::例5

Example 6 ::例6

Feature: Clean That Scrape, But Don't Get Burned ::特写: 清除那破烂, 但不要被烧伤

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Solving a System of Equations by Substitution
::以替代方式解决分配制度

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Solving a System of Equations by Substitution
::以替代方式解决分配制度

Example 5
::例5

Example 6
::例6

Feature: Clean That Scrape, But Don't Get Burned
::特写: 清除那破烂, 但不要被烧伤

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX