Section: 三个变量的解析线条系统 | 4.9 三个变量的溶解线性线性系统

Section outline

Three neighbors make a fruit salad for a summer picnic. One person uses three pounds of strawberries plus five pounds of grapes plus one pound of melon at a cost of $20. A second person uses three pounds of strawberries plus two pounds of grapes plus two pounds of melon at a cost of $21. The last neighbor uses four pounds of strawberries plus three pounds of grapes plus three pounds of melon at a cost of $30. How much does each fruit cost?
::3个邻居为夏季野餐做水果沙拉。一个人用3磅草莓加5磅葡萄加1磅瓜,费用为20美元。第二个人用3磅草莓加2磅葡萄加2磅瓜,费用为21美元。最后一个邻居用4磅草莓加3磅葡萄加3磅瓜,费用为30美元。每个水果要花多少钱?

We can solve problems like this by considering a system of three equations.
::我们可以通过考虑三个方程的系统来解决这样的问题。

Three-Dimensional Space
::三维空间

With more unknowns come more dimensions . When we have three unknowns, we need three-dimensional space for the solutions. In this section, we will focus on how to find solutions to a system of three equations algebraically and will not discuss how to find solutions graphically. However, it is useful to have an idea of the possible types of solutions in three-dimensional space or 3-space .
::随着更多未知的维度的增加,当我们有三个未知度时,我们需要三维空间来解决问题。在本节中,我们将侧重于如何找到三个方程式代数系统的解决办法,而不会以图形方式讨论如何找到解决方案。然而,了解三维空间或三空间的可能解决方案类型是有益的。

In this chapter, we have considered equations and inequalities of two variables—equations and inequalities that only required two axes laid out in a flat surface or plane. With the introduction of a third variable , we need a third axis, which we often call the z -axis . The x -axis and y -axis define the horizontal coordinate plane that you see in the image below. The z -axis increases as it points upward, that is positive values are above the origin, the O in the graph below, and the negative values are below the origin. (Note: We are assuming a right-handed orientation of the axes).
::在本章中,我们考虑了两个变量的方程式和不平等——等式和不平等,这两个变量只要求在平面或平面上标出两个轴。随着第三个变量的引入,我们需要第三个轴,我们常常称之为 z 轴。 X 轴和 y 轴定义了您在下图中看到的水平协调平面。z 轴上升时会上升,正值高于原值,下图中的O值高于正值,负值低于原值。 (注:我们假设轴向右倾)。

The axes divide the space into 8 octants. These are similar to quadrants in the coordinate plane.
::轴将空间分为8个八进制,与坐标平面上的四分位数相似。

Points in 3-space require three coordinates , $\begin{aligned} (x, y, z) \end{aligned}$ . The point plotted above is (2,3,4).
::三空点需要三个坐标(x,y,z)。上面绘制的点是(2,3,4)。

Let's consider the possible configurations for a solution to a system of three equations in 3-space.
::让我们来考虑一下三个方程式在3个空格中三个方程式的解决方案的可能配置。

Possible Forms of Solutions
::可能的解决办法的形式

An equation in three variables, such as $\begin{aligned} 2 x - 3 y + 4 z = 10 \end{aligned}$ , defines a plane in 3-space. The solution to a system of three equations is a point or points in space that satisfy all three equations, or graphically is at the intersection of all three planes. These planes could intersect with each other, or not intersect, as shown in the diagrams below.
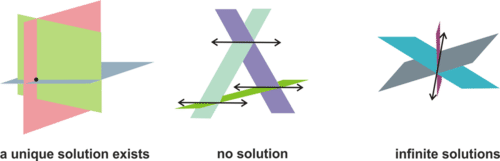
::三个变量中的方程式, 如 2x-3y+4z=10, 在 3 空格中定义一个平面。三个方程式系统中的解决方案是满足所有三个方程式的空间点或点, 或图形化的位于所有三个方程式的交叉点。如下图所示, 这些方程式可以相互交叉, 或者不相互交叉。

Possible Forms of Solutions to a System of Three Equations
::三等制可能的解决办法

Single Solution: The three planes intersect at a single point as seen in the image on the left above.

No Solutions: No solutions exist if two of the planes are parallel or if, as in the image in the center above, the planes intersect at parallel lines. In any of these cases, there is no point that is in all three planes.
::无解决方案: 如果两架飞机是平行的, 或者,如上方中心图像所示, 平面在平行线上交叉, 就没有解决方案。在其中任何一个案例中, 在所有三个平面上都没有点。

Infinite Solutions: If, as in the image on the right above, three planes intersect in a line, there are an infinite number of solutions. There can also be an infinite number of solutions if all three planes are the same.
::无限解决方案:如果像上面右边的图像一样,三平面在一行中交叉,就会有无限数量的解决方案。如果所有三个平面都相同,也可能会有无限数量的解决方案。

below by MyWhyU discusses these possibilities and shows that we can describe solutions to systems of three equations in the same way that we did with systems of two equations. If the graph of at least two of the equations are the same, then the equations are said to be dependent . When all three planes are distinct, we refer to the system as independent . If the system has at least one solution (one solution or infinitely many solutions), then it is said to be a consistent system . If the system has no solution, then it is said to be an inconsistent system .
::在 MyWaIIU 的下面讨论这些可能性, 并显示我们可以用与两个方程式相同的方式描述三个方程式系统的解决方案。如果至少两个方程式的图形相同, 那么方程式就可以说是依附的。当所有三个方程式都不同时, 我们称系统是独立的。如果系统至少有一个解决方案( 一个解决方案或无限多的解决方案), 那么它可以说是一个一致的系统。如果系统没有解决方案, 那么它就被称为一个不一致的系统。

Solving Systems of Three Equations Algebraically
::三等代数溶解系统

A solution to a system of three equations is an ordered triple, $\begin{aligned} (x, y, z) \end{aligned}$ , that makes all three equations true.
::三个方程式系统的一个解决方案是定序三重(x,y,z), 使所有三个方程式都是真的。

Example 1
::例1

Determine whether the point, (6, -2, 5), is a solution to the system below.
::确定点(6,2,5)是否是以下系统的解决办法。

\begin{aligned} x - y + z & = 13 \\ 2 x + 5 y - 3 z & = - 13 \\ 4 x - y - 6 z & = - 4 \end{aligned}

::x- y+z=132x+5y- 3z- 134x- y-6z4

Solution: In order for the point to be a solution to the system, it must satisfy each of the three equations.
::解决办法:为了找到系统的解决办法,它必须满足三个方程式中的每一个方程式。

First equation: $\begin{aligned} (6) - (- 2) + (5) = 6 + 2 + 5 = 13 \end{aligned}$
::第一等式6)-(-2)+(5)=6+2+5=13

Second equation: $\begin{aligned} 2 (6) + 5 (- 2) - 3 (5) = 12 - 10 - 15 = - 13 \end{aligned}$
::第二个方程: 2(6)+5(-2)-3(5)=12-10-1513

Third equation: $\begin{aligned} 4 (6) - (- 2) - 6 (5) = 24 + 2 - 30 = - 4 \end{aligned}$
::第三等式:4(6)-(-2)-6(5)=24+2-304

The point, (6, -2, 5), satisfies all three equations. Therefore , it is a solution to the system.
::点(6,2,5)满足了所有三个方程式,因此,这是系统的解决办法。

To solve a system of three equations in three variables, we can use a combination of the elimination by multiplication and addition and substitution methods.
::为了解决三个变数中三个方程式的系统,我们可以使用乘法、加法和替代法,将消除方法结合起来。

To Solve Systems of Three Equations
::解决三个等式的系统

1. Choose two equations and choose a variable to eliminate.
::1. 选择两个方程并选择要删除的变量。

2. Eliminate that variable in the two equations by using the elimination by multiplication and addition method. This will create a new equation with fewer variables.
::2. 通过采用乘法和加法消除这两个方程式中的变数,从而消除这两个方程式中的变数,这将产生一个新的变数较少的变数方程式。

3. Eliminate the same variable from a different combination of the equations. This will create a second new equation with fewer variables.
::3. 从不同的方程组合中除去同一个变量,这将产生第二个新的方程,变量较少。

4. Now, you have a system of two new equations with two (or fewer) unknowns. Solve the system using elimination by multiplication and addition or substitution. If there is one solution, this will result in a known value.
::4. 现在,你有一个由两个(或更少)未知的两个新方程式组成的系统。用乘法、加法或替代法来消除这个系统。如果有一个解决方案,就会产生已知值。

5. Substitute that known value into either of the equations with two variables to find another known value.
::5. 用两个变量将已知价值替代方程中的任何一个方程,以寻找另一个已知价值。

6. Substitute the two known values into any of the original equations to find the remaining unknown.
::6. 将两个已知值替换为任何原始方程,以找到其余的未知值。

Example 2
::例2

Solve the following system of equations . (This is the system from Example 1).
::解决以下方程式系统。 (这是例1中的系统)。

\begin{aligned} x - y + z & = 13 & equation 1 \\ 2 x + 5 y - 3 z & = - 13 & equation 2 \\ 4 x - y - 6 z & = - 4 & equation 3 \end{aligned}

::xy+z=13等量 12x+5y-3z13等量 24x-y-6z+4等量 3

Solution: We need to combine any two equations to eliminate one of the variables. Let's choose to eliminate y . Since the coefficient of y is -1 in the first equation, let's use that equation to eliminate y. If we consider equation 1 and equation 2, the least common multiple of the coefficients of y is 5. Since the second equation already has the LCM, we only need to multiply the first equation by 5 and then add the equations to eliminate y .
::解答: 我们需要合并任何两个方程式来消除其中的一个变量。让我们选择删除 y。由于y 系数在第一个方程式中是 - 1, 让我们使用该方程式来消除y。如果我们考虑等式 1 和等式 2, y 系数中最不常见的倍数是 5。因为第二个方程式已经拥有 LCM, 我们只需要将第一个方程式乘以 5, 然后添加等式来消除y 。

\begin{aligned} 5 (x - y + z = 13) ⟹ 5 x - 5 y + 5 z = 65 \\ 5 x - 5 y + 5 z = 65 \\ + \underline{2 x + 5 y - 3 z = - 13} \\ 7 x + 2 z = 52 & new equation 1 \end{aligned}

::5(x-y+z=13) @%5x-5y+5z=655x-5y+5z=65+2x+5y-3z}_13_7x+2z=52新方程式1

Next, let's combine equation 1 and equation 3 to get a new second equation. We need to multiply either equation 1 or equation 3 by -1 to eliminate y . We will multiply equation 1.
::接下来,让我们将方程 1和方程 3 合并来获得新的第二个方程。我们需要将方程 1 或方程 3 乘以 - 1 来消除y。我们将将方程 1 乘以等式 1 。

\begin{aligned} - 1 (x - y + z = 13) ⟹ - x + y - z = - 13 \\ - x + y - z = - 13 \\ + \underline{4 x - y - 6 z = - 4} \\ 3 x - 7 z = - 17 & new equation 2 \end{aligned}

::-1(x-y+z=13) x+y-z 13-x+y-z 13+4x-y-6z=4_3x-7z+17+2新方程式

Now, we have a system of two equations with two unknowns, x and z . We can solve this system using any of the methods we have discussed to solve a system of two equations (even graphing!). Since none of the coefficients are 1 or -1, we can continue using elimination by multiplication and addition. Since the z 's have opposite signs, let's eliminate z . The LCM for the coefficients of z is 14.
::现在,我们有一个由两个方程式组成的系统,有两个未知的方程式, x 和 z。我们可以使用我们讨论过的任何方法来解决这个系统, 解决两个方程式的系统( 偶数图形化 ! ) 。由于没有一个系数是 1 或 - 1, 我们可以继续通过乘法和加法来消除它。由于 z 有相反的信号, 我们删除z。 z 的系数的 LCM 是 14 。

\begin{aligned} 7 (7 x + 2 z = 52) ⟹ 49 x + 14 z = 364 \\ 2 (3 x - 7 z = - 17) ⟹ 6 x - 14 z = - 34 \\ 49 x + 14 z = 364 \\ + \underline{6 x - 14 z = - 34} \\ 55 x = 330 \\ x = 6 \end{aligned}

::7( 7x+2z=52) 49x+14z=3642( 3x-7z17) 6x-14z}}3449x+14z=364+ 6x-14z=34_55x=330x=6

With one solution, we can start to find the other two unknowns. Substituting into new equation 1 gives us

::有了一种解决办法,我们就可以开始找到另外两个未知因素。

\begin{aligned} 7 (6) + 2 z = 52 \\ 42 + 2 z = 52 \\ 2 z = 10 \\ z = 5 \end{aligned}

::7(6)+2z=5242+2z=522z=10z=5

To find y , we can substitute x and z into the original equation 1.
::为了找到y,我们可以将x和z替换为原方程1。

\begin{aligned} x - y + z = 13 \\ 6 - y + 5 = 13 \\ 11 - y = 13 \\ - y = 2 \\ y = - 2 \end{aligned}

::x-y+z=136-y+5=1311-y=13-y=13-y=2y=2y2

Our last step would be to check the solution by substituting the values for x, y, and z as we did in Example 1.
::我们的最后一步是检查解决办法,按照例1中的做法,用x、y和z的值取代x、y和z。

by CK-12 demonstrates how to solve systems in three variables using elimination.
::通过 CK-12 演示如何用除去来解析三个变量中的系统。

Example 2
::例2

Solve the following system of equations.
::解决以下方程式系统。

\begin{aligned} 2 x + 4 y - 3 z & = - 7 & equation 1 \\ 3 x - y + z & = 20 & equation 2 \\ x + 2 y - z & = - 2 & equation 3 \end{aligned}

::2x+4y-3z7等量 13x-y+z=20等量 2x+2y-z2等量 3

Solution: We can start by taking two equations at a time and eliminating the same variable. We can take the first two equations and eliminate $\begin{aligned} z \end{aligned}$ , then take the second and third equations and also eliminate $\begin{aligned} z \end{aligned}$ .
::解答: 我们可以从一次使用两个方程式开始, 并删除同一个变量。我们可以使用前两个方程式, 删除 Z, 然后使用第二和第三个方程式, 并删除 z 。

\begin{aligned} 2 x + 4 y - 3 z = - 7 ⟹ 2 x + 4 y - 3 z = - 7 \\ 3 (3 x - y + z = 20) + \underline{9 x - 3 y + 3 z = 60} \\ 11 x + y = 53 \end{aligned}

::2x+4y-3z72x+4y-3z73(3x-y+z=20)+9x-3y+3z=60_11x+y=53

The result from combining equations 1 and 2 is our new equation 1: $\begin{aligned} 11 x + y = 53 \end{aligned}$
::合并方程1和2的结果是我们新的方程1: 11x+y=53

\begin{aligned} 3 x - y + z = 20 \\ \underline{x + 2 y - z = - 2} \\ 4 x + y = 18 \end{aligned}

::3 - y+z=20x+2y - z2 - 4x+y=18 3 - y+z=20x+2y - z2 - 4x+y=18

The result from combining equations 2 and 3 is our new equation 2: $\begin{aligned} 4 x + y = 18 \end{aligned}$
::合并方程2和3的结果是我们新的方程2: 4x+y=18

We have reduced our system to two new equations in two variables. We can eliminate $\begin{aligned} y \end{aligned}$ next and solve for $\begin{aligned} x \end{aligned}$ .
::我们已经将我们的系统简化为两个变量中的两个新方程式。我们可以删除 y 下一个变量, 并解决 x 。

\begin{aligned} 11 x + y = 53 \Rightarrow 11 x + y = 53 \\ - 1 (4 x + y = 18) + \underline{- 4 x - y = - 18} \\ 7 x = 35 \\ x = 5 \end{aligned}

::11x+y=5311x+y=53-1(4x+y=18) 4x-y18_7x=35x=5

Now using this value in new equation 2 to find $\begin{aligned} y \end{aligned}$ :
::现在在新方程式 2 中使用此值查找 y :

\begin{aligned} 4 (5) + y & = 18 \\ 20 + y & = 18 \\ y & = - 2 \end{aligned}

::4(5)+y=1820+y=18y @%2

Finally, we can go back to one of the original three equations, say equation 1, and use our $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values to find $\begin{aligned} z \end{aligned}$ .
::最后,我们可以回到原来的三个方程中的一个, 比如方程1, 用我们的x值和y值来找到z。

\begin{aligned} 2 (5) + 4 (- 2) - 3 z & = - 7 \\ 10 - 8 - 3 z & = - 7 \\ 2 - 3 z & = - 7 \\ - 3 z & = - 9 \\ z & = 3 \end{aligned}

::2(5)+4(-2)-3z710-8-3z72-3z7-3z7-3z9z=3

The solution is (5, -2, 3).
::解决办法是5,2,3。

Checking the answer by substituting the values into each equation confirms our solution.
::通过在每个方程式中替换值来检查答案,证实了我们的解决方案。

Equation 1: $\begin{aligned} 2 (5) + 4 (- 2) - 3 (3) = 10 - 8 - 9 = - 7 \end{aligned}$
::等式1: 2(5)+4(-2-2)-3(3)=10-8-97

Equation 2: $\begin{aligned} 3 (5) - (- 2) + (3) = 15 + 2 + 3 = 20 \end{aligned}$
::等式2: 3(5)-(-2)+(3)=15+2+3=20

Equation 3: $\begin{aligned} (5) + 2 (- 2) - (3) = 5 - 4 - 3 = - 2 \end{aligned}$
::等式35)+2(-2)-(3)=5-4-32

by Mathispower4u demonstrates how to solve systems in three variables and shows how to represent the solution graphically .
::通过 Mathispower4u 演示如何用三个变量解析系统, 并演示如何以图形方式代表解决方案。

Example 3
::例3

Solution: The system of linear equations represented by this situation is below, where s , g , and m represent the cost of strawberries, grapes and melons, respectively.
::解决办法:这种情况所代表的线性方程式系统如下:草莓、葡萄和瓜的成本分别为 s、g和m。

\begin{aligned} 3 s + 5 g + m = 20 \\ 3 s + 2 g + 2 m = 21 \\ 4 s + 3 g + 3 m = 30 \end{aligned}

::3s+5g+m=203s+2g+2m=214s+3g+3m=30

We can eliminate one of the variables by using substitution rather than elimination by multiplication and addition. Since the coefficient of m is 1 in the first equation, we can solve for m and get
::我们可以通过使用替代而不是通过乘法和加法来消除其中的一个变量。由于 m 系数在第一个方程中是1, 我们可以解决m, 并获得

\begin{aligned} m = 20 - 2 s - 5 g \end{aligned}

::m=20-2s-5g

Now we can substitute this value for m into the other two equations. When we do so we get a new system of linear equations:
::现在我们可以用这个值代替 m, 换成另外两个方程式。当我们这样做的时候, 我们得到一个新的线性方程式系统 :

$\begin{aligned} 3 s + 2 g + 2 (20 - 2 s - 5 g) = 21 \\ 4 s + 3 g + 3 (20 - 2 s - 5 g) = 30 \end{aligned}$

::3s+2g+2(20-20-2s-5g)=214s+3g+3(20-2s-5g)=30

Simplifying both equations results in two new equations.
::简化两个方程式导致两个新的方程式。

\begin{aligned} - s - 8 g = - 19 \\ - 2 s - 12 g = - 30 \end{aligned}

::-s -8g19 -2s -12g30

We can solve this system using elimination by multiplication and addition. If we multiply the first of these equations by –2, we get the new system of equations

::我们可以用乘法和加法来消除这个系统。如果我们把第一个等式乘法乘以- 2, 我们就可以得到新的等式系统

\begin{aligned} 2 s + 16 g = 38 \\ + \underline{- 2 s - 12 g = - 30} \\ 4 g = 8 \\ g = 2 \end{aligned}

::2s+16g = 382s-12g = 30_4g = 8g= 2

Next, we can substitute this value of g into either of the two new equations to get the value of s.
::接下来,我们可以用这个g值来替代两个新方程中的任何一个, 以获得 s值。

\begin{aligned} - 2 s - 12 (2) = - 30 \\ - 2 s - 24 = - 30 \\ - 2 s = - 6 \\ s = 3 \end{aligned}

::-2-12(2)30-2s-2430-2s6s=3

Finally, we substitute these values for g and s into one of our original equations.
::最后,我们用这些数值来代替g和s 来取代我们原来的方程之一。

\begin{aligned} 2 (3) + 5 (2) + m = 20 \\ 6 + 10 + m = 20 \\ 16 + m = 20 \\ m = 4 \end{aligned}

::2(3)+5(2)+m=206+10+m=2016+m=20m=4

Therefore, strawberries cost $3 per pound, grapes cost $2 per pound, and melon costs $4 per pound.
::因此草莓每磅3美元,葡萄每磅2美元,瓜每磅4美元。

by CK-12 demonstrates how to solve systems in three variables by using substitution with one solution.
::使用 CK-12 来演示如何用一个解决方案替代三个变量的系统。

Example 4
::例4

Solve the following system of equations.

\begin{aligned} x + y + z & = 5 \\ 5 x + 5 y + 5 z & = 20 \\ 2 x + 3 y - z & = 8 \end{aligned}

::解决以下方程系统。 x+y+z=55x+5y+5z=202x+3y-z=8

Solution: We can start by combining equations 1 and 2 together by multiplying the first equation by -5.
::解答:我们可以将方程式1和2结合起来, 将第一个方程式乘以 - 5。

\begin{aligned} - 5 (x + y + z = 5) ⟹ - 5 x - 5 y - 5 z = - 25 \\ 5 x + 5 y + 5 z = 20 + \underline{5 x + 5 y + 5 z = 20} \\ 0 = - 5 \end{aligned}

::5(x+y+z=5) 5(x+y+z=5) 5(%) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5)+5(5) 5(5) +5(5) 5(5) 5(5) 5(5) 5(5) 5(5) +(5) +(5) +(5) 5(5) +(5) 5(5) 5(5) 5(5(5) 5(5) 5(5) 5(5(5) 5(5) 5(5) 5(5) 5(5) 5(5(5(5) 5) 5) 5(5(5) (5) 5(5(5) 5(5) 5) (5) 5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5) (5

Since the result is a false equation, there is no solution to the system. If you end up with 0 = 0, then there will be infinitely many solutions.
::由于结果是一个虚假的等式, 系统就没有解决方案。如果您以 0 = 0 结尾, 那么将会有很多解决方案。

by Mathispower4u provides examples of a system with no solutions and infinite solutions. The answers are verified graphically.
::由 Mathispower4u 提供一个没有解决方案和无限解决方案的系统的例子。答案通过图形验证。

Feature: The Perfect Hue
::特色:完美色调

by Deirdre Mundy
::由Deirdre Mundy 编辑

Have you ever painted a room? Before you start painting, you have to carefully choose a color. You then head over to a hardware or paint store and ask the staff to mix the color for you. The store does not keep every color in stock at all times. How can the staff mix up the right color on a moment’s notice?
::你画过房间吗? 在开始绘画之前, 您必须仔细选择一个颜色。然后去一个硬件或油漆商店, 请员工混合您的颜色。商店不总是保存所有的颜色。员工如何在一瞬间通知时混合正确的颜色 ?

Mixing Machines
::混合机

At most large stores, staff members use a mixing machine to create your paint. Paint consists of a base and pigment. The base is usually white. It gives the paint body and helps it stick to the wall. The pigment gives the paint its color. By carefully combining pigments, the store can produce almost any color imaginable. The mixing machine uses systems of equations to determine how much of each pigment, usually red, blue, and yellow, to use in order to produce a set amount of a given color. More pigment makes brighter, darker colors. Less pigment makes lighter colors.
::在大多数大型商店,工作人员使用混合机器来制造你的油漆。油漆由底色和颜料组成。底色通常是白色的。它给油漆身体, 帮助它粘在墙上。颜料给它颜色。通过仔细结合颜料, 商店几乎可以产生任何可以想象的颜色。混合机器使用方程系统来确定每个色料( 通常是红色、蓝色和黄色) 的多少, 用来产生一定的颜色。更多的颜料让颜色更亮, 更暗。更少的色素会更淡。

When you are decorating a room, it is important to choose your colors carefully. Scientists have studied how different colors affect the brain. Red rooms actually cause students to perform worse on exams, while green rooms improve reading comprehension scores. Pink walls calm people down for short periods of time but make them angry in the long run . Blue walls can control appetite, and yellow walls can make adults anxious and babies cry.
::当您正在装饰一个房间时,必须仔细选择您的颜色。科学家们研究了不同颜色如何影响大脑。红色房间实际上让学生在考试中表现更差,而绿色房间则提高了阅读理解分数。粉色墙让人们在短时期内平静下来,但从长远看却让他们愤怒。蓝墙可以控制胃口,黄色墙会让成年人焦虑不安和婴儿哭泣。

by Country Chic Paint demonstrates how to mix paint.
::以Chic 国家为单位,涂料展示了如何混合涂料。

Summary
::摘要

Three-dimensional space is made up of three intersecting number lines. Points in 3-space are of the form $\begin{aligned} (x, y, z) \end{aligned}$ .
::三维空间由三条交叉数字线组成。三维空间的点为形式(x,y,z)。

Linear systems of three variables can have three possible solutions—one, none, or infinite.
::三个变数的线性系统可以有三个可能的解决办法——一个,一个,一个,或无限。

To solve a system of three linear equations, reduce the system to two equations with two unknowns either by elimination by multiplication and addition or by substitution. Then, solve as a system of two linear equations. Substitute to find the missing values.
::要解决由三个线性方程式组成的系统, 将系统缩小为两个未知方程式, 两个未知方程式, 要么通过乘法和加法来消除, 要么通过替换来消除。然后, 以两个线性方程式的系统来解析。替代以寻找缺失值。

Review
::回顾

Solve the following systems in three variables.
::在三个变量中解决以下系统。

1.
$\begin{aligned} \begin{aligned} 11 x + 15 y + 5 z = 1 \\ 3 x + 4 y + z = - 2 \\ 7 x + 13 y + 3 z = 3 \end{aligned} \end{aligned}$
::1. 1x+15y+5z=13x+4y+z27x+13y+3z=3

2.
$\begin{aligned} \begin{aligned} 2 x + y + 7 z & = 5 \\ 3 x - 2 y - z & = - 1 \\ 4 x - y + 3 z & = 5 \end{aligned} \end{aligned}$
::2. 2x+y+7z=53x-2y-z14x-y+3z=5

3.
$\begin{aligned} \begin{aligned} x + 3 y - 4 z = - 3 \\ 2 x + 5 y - 3 z = 3 \\ - x - 3 y + z = - 3 \end{aligned} \end{aligned}$
::3. x+3y-4z32x+5y-3z=3-x-3y+z3

4.
$\begin{aligned} \begin{aligned} 3 x + 2 y - 5 z = - 8 \\ 3 x + 2 y + 5 z = - 8 \\ 6 x + 4 y - 10 z = - 16 \end{aligned} \end{aligned}$
::4. 3x+2y-5z83x+2y+5z86x+4y-10z16

$\begin{aligned} \begin{aligned} x + 2 y - z = - 1 \\ 2 x + 4 y + z = 10 \\ 3 x - y + 8 z = 6 \end{aligned} \end{aligned}$
::x+2y-zZ12x+4y+z=103x-y+8z=6

$\begin{aligned} \begin{aligned} x + y + z = - 3 \\ 2 x - y - z = 6 \\ 4 x + y + z = 0 \end{aligned} \end{aligned}$
::x+y+z+z%32x-y-z=64x+y+z=0

$\begin{aligned} \begin{aligned} 4 x + y + 3 z = 8 \\ 8 x + 2 y + 6 z = 15 \\ 3 x - 3 y - z = 5 \end{aligned} \end{aligned}$
::4x+y+3z=88x+2y+6z=153x-3y-z=5

$\begin{aligned} \begin{aligned} 2 x + 3 y - z & = - 1 \\ x - 2 y + 3 z & = - 4 \\ - x + y - 2 z & = 3 \end{aligned} \end{aligned}$
::2x+3y-z1x-2y+3z4-x+y-2z=3

9.
$\begin{aligned} \begin{aligned} x - 3 y + 4 z = 14 \\ - x + 2 y - 5 z = - 13 \\ 2 x + 5 y - 3 z = - 5 \end{aligned} \end{aligned}$
::9. x-3y+4z=14-x+2y-5z132x+5y-3z5

10.

$\begin{aligned} \begin{aligned} x + y + z = 3 \\ x + y - z = 3 \\ 2 x + 2 y + z = 6 \end{aligned} \end{aligned}$
::x+y+z=3x+y-z=32x+2y+z=6

Explore More
::探索更多

1. Three sets of triathlon teams are competing in separate triathlon legs, a swim, a bike, and a run, for their training. The speeds of the participants and the total distance covered by the team are in the table below.
::1. 三组三人队以三重腿、游泳、自行车和跑步进行比赛,以进行训练,参加者的速度和总距离见下表。

Team	Swim	Bike	Run	Total Distance Covered by Team
1	2 mph	17 mph	7.5 mph	47.75 miles
2	1.5 mph	20 mph	7 mph	52.375 miles
3	1.25 mph	18 mph	8 mph	49.5625 miles

How much time is each leg of the training race? (Hint: Use $\begin{aligned} d = r t \end{aligned}$ , distance=rate x time, to set up the equations.)
::每段训练赛程需要多少时间? (提示: 使用 d=rt、距离=率 x 时间来设置方程。 )

2. A farmer rotates wheat, corn, and soybean crops on her farm ¹ . The farmer produces 293 bushels of produce and sells them for a total of $1,557. Wheat costs $8 for a bushel. Corn costs $4 a bushel. Soybeans cost $9 a bushel. If the farmer's crops yield 4.75 times more corn than wheat, how many bushels of each crop does the farmer produce?
::2. 农民在自己的农场上轮流种植小麦、玉米和大豆作物。农民生产293桶农产品,销售价值共计1 557美元,小麦8美元,小麦4美元,玉米4美元,小麦9美元,大豆9美元,农民作物的玉米产量是小麦的4.75倍,农民生产多少桶?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:

References
::参考参考资料

1. "Adding Wheat to Corn-Soybean Rotations Helps Control Pests," published November 18, 2014, http://www.agriculture.com/crops/wheat/adding-wheat-to-cnsoybe-rotations-helps_144-ar46231.
::1. 2014年11月18日发表的《将小麦添加到玉米-豆类轮流帮助控制害虫》,http://www.agriculture.com/crops/wheat/adding-wheat-to-cnsoybe-rotations-helps_144-ar46231。

Section outline

Three-Dimensional Space ::三维空间

Possible Forms of Solutions ::可能的解决办法的形式

Possible Forms of Solutions to a System of Three Equations ::三等制可能的解决办法

Solving Systems of Three Equations Algebraically ::三等代数溶解系统

Example 1 ::例1

To Solve Systems of Three Equations ::解决三个等式的系统

Example 2 ::例2

Example 2 ::例2

Example 3 ::例3

3 s + 2 g + 2 ( 20 − 2 s − 5 g ) = 21 4 s + 3 g + 3 ( 20 − 2 s − 5 g ) = 30 ::3s+2g+2(20-20-2s-5g)=214s+3g+3(20-2s-5g)=30

Example 4 ::例4

Feature: The Perfect Hue ::特色:完美色调

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

References ::参考参考资料

Three-Dimensional Space
::三维空间

Possible Forms of Solutions
::可能的解决办法的形式

Possible Forms of Solutions to a System of Three Equations
::三等制可能的解决办法

Solving Systems of Three Equations Algebraically
::三等代数溶解系统

Example 1
::例1

To Solve Systems of Three Equations
::解决三个等式的系统

Example 2
::例2

Example 2
::例2

Example 3
::例3

$\begin{aligned} 3 s + 2 g + 2 (20 - 2 s - 5 g) = 21 \\ 4 s + 3 g + 3 (20 - 2 s - 5 g) = 30 \end{aligned}$

::3s+2g+2(20-20-2s-5g)=214s+3g+3(20-2s-5g)=30

Example 4
::例4

Feature: The Perfect Hue
::特色:完美色调

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX

References
::参考参考资料