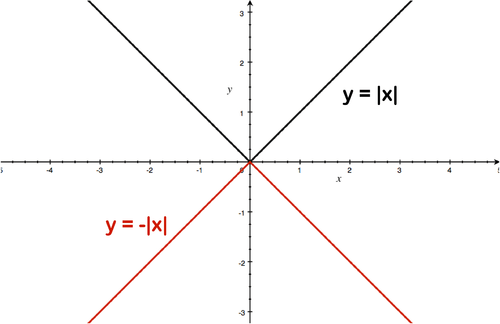Section: 图图的变形 | 5.7 图图的变换

Section outline

Sometimes computer animators take an image and copy it to some other location on the screen. They can enlarge or shrink it. They can flip it upside down. We learn how to do these transformations of a graph in this section.
::有时计算机动画师将图像复制到屏幕上的其他位置。他们可以放大或缩小它。他们可以翻转它倒过来。我们学习如何对本节中的图表进行这些转换。

Transformations
::变换

A transformation is resizing or moving a basic graph in the coordinate plane . In this section, we will mostly consider those changes to a graph we have already seen—the absolute value graph, but this is a concept you will apply to many of the functions that we consider in the remainder of the book. We will start with rigid transformations. Those are transformations that preserve the shape of the original graph. Then, we will consider non-rigid transformations —transformations that distort the original shape of the graph.
::转换正在调整或移动坐标平面上的基本图形。在本节中, 我们主要会考虑已经看到的图形中的这些变化—— 绝对值图形, 但是这个概念会适用于我们这本书剩余部分中考虑的许多函数。我们将从僵硬的变换开始。这些变换是保留原始图形形状的变换。然后, 我们将考虑非硬化变换—— 扭曲图形原始形状的变换。

Translations
::笔译翻译

A translation is a shift to the right or the left, up or down.
::翻译是向右或向左、向上或向下转换。

Example 1
::例1

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when you graph $\begin{aligned} y = | x | + 3 \end{aligned}$ ?
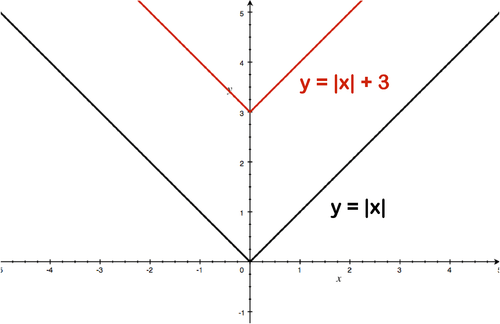
::当你绘制 y x 3 的图时, y x 3 的变形会怎样?

Solution: As we can see in the graph below, the point (0,0) moved up 3 units and is now the point (0,3). The original graph $\begin{aligned} y = | x | \end{aligned}$ , graphed in black below, has been shifted up 3 units to create the new graph in red below.
::解答:如下图所示,点(0,0)向上移动了3个单位,现在是点(0,3)。原图 yx,以下面的黑色为图表,已经向上移动了3个单位,以创建下面红色的新图。

Example 2
::例2

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when you graph $\begin{aligned} y = | x | - 4 \end{aligned}$ ?
::当你绘制 y x 4 的图时, y x 4 的变形会怎样?

Solution: Notice how the point (0,0) moved down 4 units and became (0,4). The original graph $\begin{aligned} y = | x | \end{aligned}$ has been shifted down 4 units.
::解决方案: 注意点( 0,0) 如何向下移动 4 个单位, 并变成 0, 4 个单位。原始图 y x 已向下移动 4 个单位。

Vertical Translations or Shifts
::垂直翻转或 Shift

To shift a graph up or down, you add or subtract a value from y. When you add, the graph goes up. When you subtract, the graph goes down.
::要向上或向下移动图表,您可从 y 中增加或减去一个数值。当添加时,图形会向上移动。当减去时,图形会向下移动。当减去时,图形会向下移动。

$\begin{aligned} y = f (x) \pm k & k > 0 \end{aligned}$

::y=f( x) kk>0

Example 3
::例3

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when you graph $\begin{aligned} y = | x - 2 | \end{aligned}$ ?
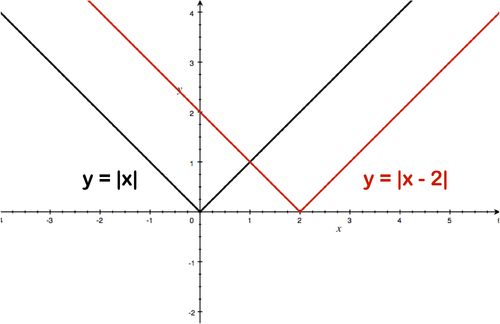
::当你绘制 y x - 2 时, y x 发生什么变化 ?

Solution: Here the point (0,0) moves to the right 2 units. The original graph has been shifted to the right 2 units.
::解答: 在这里, 点( 0, 0) 移动到右侧 2 个单位。原始图形已被移到右侧 2 个单位。

Example 4
::例4

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when you graph $\begin{aligned} y = | x + 3 | \end{aligned}$ ?
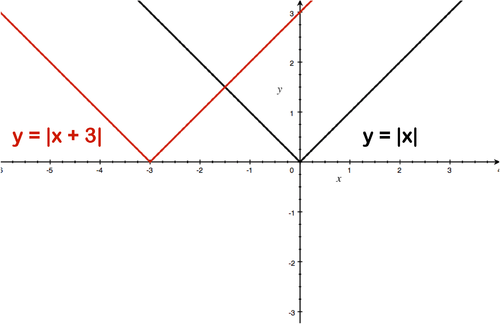
::当您绘制 yx+3时, yx会发生什么变化 ?

Solution: The graph has been shifted to the left 3 units, including (0,0) which is now (-3,0).
::解答:图表已移到左3个单元,包括(0,0),现在是(3,30)。

Horizontal Translations or Shifts
::水平翻转或移动

To shift a graph to the right or to the left, you add or subtract a value from x . When you add, the graph shifts to the left. When you subtract, the graph shifts to the right.
::要将图表向右或向左移动,您将从 x 中增加或减去一个数值。添加时,图形向左移动。减去后,图形向右移动。

(Be careful! This is probably the opposite of how you think it would work.)
:小心点!这或许与你所想的正好相反。 )

$\begin{aligned} y = f (x \pm h) & h > 0 \end{aligned}$

::y=f( xh) h>0

by Mathispower4u demonstrates how to graph horizontal and vertical translations.
::由 Mathispower4u 演示如何绘制水平和垂直翻译。

Reflections
::反思

A reflection creates the same graph an equal but opposite distance from a particular line or point. This is similar to looking at yourself in the mirror. The mirror is the particular line that our image is reflected across. We will consider two types of reflections—those across the x -axis and those across the y -axis.
::反射产生与特定线条或点相同但相对的距离。这与在镜子中看着你自己相似。镜子是我们形象的反射线。我们将考虑两种反射类型 — — 横跨 X 轴和横跨 y 轴的反射。

Example 5
::例5

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when you graph $\begin{aligned} y = - | x | \end{aligned}$ ?
::当您用图表绘制您时您的变形会怎样?

Solution: The graph is reflected across the x -axis. Notice how the point (1,1) became the point (-1,1).
::解析度 : 图形在 X 轴中反射。注意点(1, 1) 是如何变成点(1, 1) 的。

Example 6
::例6

What transformation happens to the graph of $\begin{aligned} y = \sqrt{x} \end{aligned}$ when you graph $\begin{aligned} y = \sqrt{- x} \end{aligned}$ ?
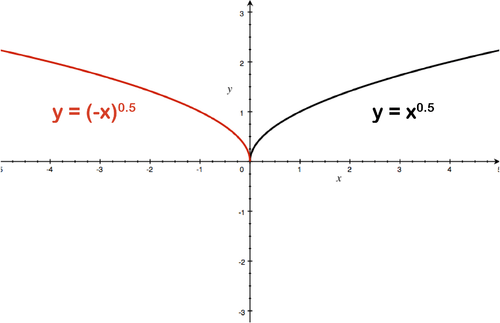
::y=x 的图形在图形 y =x 时会发生什么变化 ?

Solution: The graph in black below is reflected across the y -axis and becomes the graph in red below. Here (9,3) becomes (-9,3).
::解答: 下面黑色的图表在 Y 轴上反射, 变成下面红色的图表。这里( 9 3) 变成 ( 9 3) 。

Reflections
::反思

When you negate y , you reflect about the x -axis. When you negate x , you reflect about the y -axis.
::当否定 y 时, 你反省 X 轴。当否定 x 时, 你反省 y 轴。

$\begin{aligned} y = - f (x) & reflection about the x-axis \\ y = f (- x) & reflection about the y-axis \end{aligned}$

::y- 轴的 yf( x) reflection 关于 x- axisy=f( x) reflection 关于 y- 轴的 y- 轴的 yf( x) reflection

by Mathispower4u demonstrates how to graph reflections across the x- axis and y- axis.
::由 Mathispower4u 演示如何绘制 X 轴和 Y 轴的反射图。

Dilations
::关系

A dilation is a transformation where each of the x -values or y- values is multiplied by a scalar factor or number. This is an example of a non-rigid transformation.
::放大法是指每个 X 值或 Y 值乘以一个星标系数或数字的变异。这是一个非硬化变异的例子。

We will focus on vertical dilations where the y -values are multiplied by a scalar factor. Most horizontal dilations can be thought of in terms of vertical dilations, and the best examples of horizontal dilations are in trigonometry, which is outside of the scope of this book. Also, other books use terminology like stretch , compression and shrink for dilations, but since there is no consistency or standard, these will be avoided.
::我们将关注垂直扩张, 即 Y 值乘以一个天平系数。大多数水平扩张可以以垂直扩张方式来考虑, 而横向扩张的最佳例子则是三角法, 这不属于本书的范围。另外, 其他的书籍使用延缩、压缩和缩缩等术语来进行扩张, 但是因为没有一致性或标准, 这些将被避免。

Example 7
::例7

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when we graph $\begin{aligned} y = 2 | x | \end{aligned}$ ?
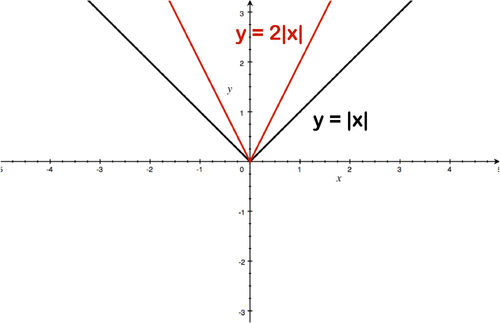
::当我们绘制 y=2\\\\\\\\\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 发生什么变化?

Solution: The y -values get bigger by a factor of 2. For instance, the point (3,3) becomes the point (3,6).
::解答:Y值乘以2而增大,例如,点(3,3)成为点(3,6)。

Example 8
::例8

What transformation happens to $\begin{aligned} y = | x | \end{aligned}$ when we graph $\begin{aligned} y = \frac{1}{2} | x | \end{aligned}$ ?
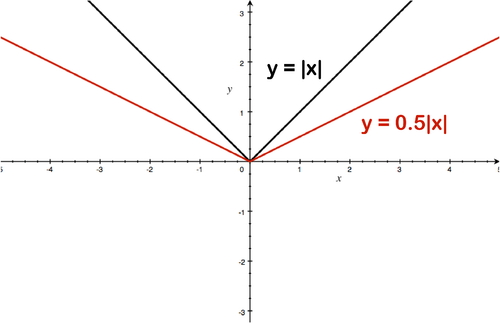
::当我们绘制y=12x时 yx会发生什么变化?

Solution: The y -values get smaller by a factor of 2. The point (1,1) becomes the point (1, $\begin{aligned} \frac{1}{2} \end{aligned}$ ).
::解决方案: Y 值变小为 2 系数。点(1, 1) 成为点(1, 12 )。

Vertical Dilations
::垂直垂直关系

When you multiply the function by a number greater than 1, the y -values go up. When you multiply the function by a number between 0 and 1, the y -values go down.
::当函数乘以大于1的数时,Y值会上升。当函数乘以0和1之间的数时,y值会下降。

$\begin{aligned} y = a f (x) & a > 1 & y-values go up \\ 0 < a < 1 & y-values go down \end{aligned}$

::y=af(x) a>1y-value 值向上上升0<a<a<1y-value 向下下降

by CK-12 demonstrates example of dilations.
::以 CK-12 显示的放大示例。

Combining The Transformations Together
::将变革结合在一起

Now that we have several transformations, the question is how to tackle more than one transformation at a time.
::现在我们有几种转变,问题是如何一次处理不止一种转变。

Combining the Transformations
::合并转型

$\begin{aligned} y = a f (x \pm h) \pm k & h > 0, k > 0 \end{aligned}$
Perform the transformations in the following order :
::y=af( xh) kh>0,k>0Perform 转换按以下顺序排列:

1. Reflections
::1. 反思

2. Dilations
::2. 关系

3. Horizontal shifts
::3. 横向转移

4. Vertical shifts
::4. 纵向转移

Example 7
::例7

Sketch the graph of $\begin{aligned} y = - | x + 2 | - 3 \end{aligned}$ .
::绘制 yx+23 的图形。

Solution: To sketch $\begin{aligned} y = - | x + 2 | - 3 \end{aligned}$ , start with the parent equation : $\begin{aligned} f (x) = | x | \end{aligned}$ .
::解答: 绘制 yx+23, 从父方程式开始 : f( x) x 。

First reflect over the x -axis:
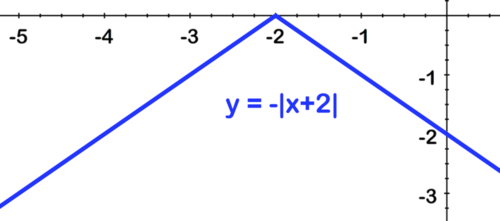
::首先反射 X 轴 :

Second, shift left by 2:
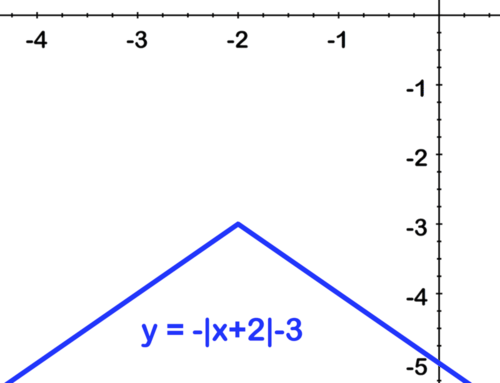
::第二,左转2:

Finally, shift down by 3:
::最后,下调3:

by Mathispower4u shows examples of graphing using transformations.
::在 Mathispower4u 中显示使用变换的图形化示例。

Summary
::摘要

Vertical shift: Add or subtract a value from $\begin{aligned} f (x) \end{aligned}$ .
::垂直移动: 从 f(x) 中添加或减去值。

Horizontal shift: Add or subtract a value from x .
::水平移动:从 x 中添加或减去一个值。

Reflect about x -axis: Negate $\begin{aligned} f (x) \end{aligned}$ .
::反射 X 轴 : Negate f( x) 。

Reflect about y -axis: Negate x .
::反射 Y 轴: Negate x 。

Dilation: Multiply $\begin{aligned} f (x) \end{aligned}$ by a constant.
::膨胀: 乘以 f(x) 值乘以一个常数。

The order to perform the transformations in is reflections, dilations, horizontal shifts and lastly vertical shifts.
::进行转换的顺序是反射、推算、水平移动和最后垂直移动。

Review
::回顾

Describe the three transformations given the formula.
::描述给定公式的三个变换。

1. $\begin{aligned} y = 4 f (- x) - 3 \end{aligned}$
::1.y=4f(-x)-3

2. $\begin{aligned} y = - f (x - 2) + 5 \end{aligned}$
::2. yf(x-2)+5

3. $\begin{aligned} y = \frac{1}{2} f (x + 3) - 1 \end{aligned}$
::3. y=12f( x+3)--1

4. $\begin{aligned} y = - 2 f (x + 4) \end{aligned}$
::4. y2f(x+4)

5. $\begin{aligned} y = - f (- x) + 4 \end{aligned}$
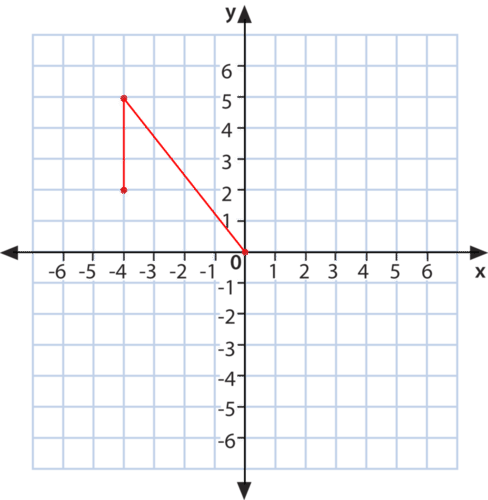
::5. yf(-x)+4

Given the following graph of $\begin{aligned} f (x) \end{aligned}$ , apply the transformations below.
::鉴于 f(x) 的下图,应用以下的变换。

6. $\begin{aligned} f (x - 2) + 1 \end{aligned}$
::6. f(x-2)+1

7. $\begin{aligned} f (- x) \end{aligned}$
::7.f(x)

8. $\begin{aligned} f (x + 1) - 2 \end{aligned}$
::8. f(x+1)-2

9. Describe the transformation that would change $\begin{aligned} f (x) \end{aligned}$ in the following ways:
::9. 说明以下列方式改变f(x)的变换:

Dilation by a factor of 2.
::膨胀乘以 2 。

Vertical shift up 3 units.
::垂直向上移动3个单元。

Horizontal shift right 2 units.
::水平向右移动 2 个单位。

10. Describe the transformation that would change $\begin{aligned} f (x) \end{aligned}$ in the following ways:
::10. 说明以下列方式改变f(x)的变换:

Vertical reflection across the x -axis.
::X轴的垂直反射。

Vertical shift down 1 unit.
::垂直向下移动 1 个单位。

Horizontal shift left 2 units.
::横向左转 2 个单位。

11. Describe the transformation that would change $\begin{aligned} g (x) \end{aligned}$ in the following ways:
::11. 描述以下列方式改变g(x)的变换:

Dilation by a factor of 4.
::膨胀乘以4 乘以4 。

Reflection across the y- axis.
::横跨Y轴反射

12. Describe the transformation that would change $\begin{aligned} k (x) \end{aligned}$ in the following ways:
::12. 描述以下列方式改变 k(x) 的变换:

Dilation by a factor of 3.
::膨胀乘以3 乘以3

Vertical shift up 3 units.
::垂直向上移动3个单元。

Horizontal shift right 2 units.
::水平向右移动 2 个单位。

13. Describe the transformation that would change $\begin{aligned} h (x) \end{aligned}$ in the following ways:
::13. 说明以下列方式改变h(x)的转变:

Dilation by a factor of $\begin{aligned} \frac{1}{4} \end{aligned}$ .
::膨胀系数为14。

Reflection across the x -axis.
::反射到X轴上方

Horizontal shift left 1 unit.
::左1单位水平向左移动。

Answers for Review Problems
::回顾问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:

Section outline

Transformations ::变换

Translations ::笔译翻译

Example 1 ::例1

Example 2 ::例2

Vertical Translations or Shifts ::垂直翻转或 Shift

Example 3 ::例3

Horizontal Translations or Shifts ::水平翻转或移动

Reflections ::反思

Example 5 ::例5

Example 6 ::例6

Reflections ::反思

Dilations ::关系

Example 7 ::例7

Example 8 ::例8

Vertical Dilations ::垂直垂直关系

Combining The Transformations Together ::将变革结合在一起

Combining the Transformations ::合并转型

Example 7 ::例7

Summary ::摘要

Review ::回顾

Answers for Review Problems ::回顾问题的答复

PLIX ::PLIX

Transformations
::变换

Translations
::笔译翻译

Example 1
::例1

Example 2
::例2

Vertical Translations or Shifts
::垂直翻转或 Shift

Example 3
::例3

Horizontal Translations or Shifts
::水平翻转或移动

Reflections
::反思

Example 5
::例5

Example 6
::例6

Reflections
::反思

Dilations
::关系

Example 7
::例7

Example 8
::例8

Vertical Dilations
::垂直垂直关系

Combining The Transformations Together
::将变革结合在一起

Combining the Transformations
::合并转型

Example 7
::例7

Summary
::摘要

Review
::回顾

Answers for Review Problems
::回顾问题的答复

PLIX
::PLIX