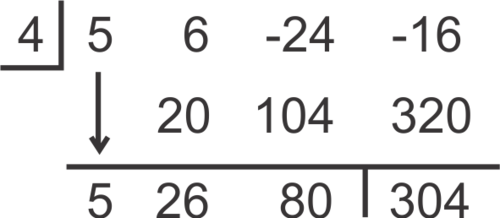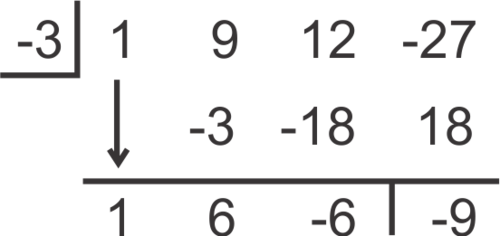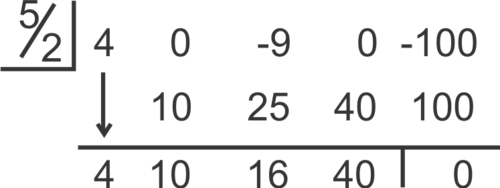Section: 多多边合成科合成科 | 6.7 多元体合成部

Section outline

Thanks to the work of Paolo Ruffini in the 1800's, we have a shorter way of performing division of when the divisor is of the form $\begin{aligned} x - k \end{aligned}$ ¹ . We consider the special case of synthetic division called Ruffini's Rule in this section.
::由于保罗·鲁菲尼在1800年代所做的工作,我们有一个较短的分工方式,即分出X-k1表的区划,我们在本节中考虑了合成区划称为鲁菲尼规则的特例。

Synthetic Division
::合成司

Synthetic division is an alternative to long division from the previous concept. With synthetic division, the variables are removed and the calculation focuses on the coefficients. While synthetic division can be used for divisors like quadratics or other higher- degree polynomials, we will focus on the special, and useful, case where the divisor is of the form $\begin{aligned} x - k \end{aligned}$ .
::合成分裂是取代前一个概念的长分割的替代方法。合成分裂随着合成分裂,变数被删除,而计算的重点是系数。虽然合成分裂可以用于四边形或其他高度多面体等三边形,但我们将侧重于特殊和有用的案例,即三角形为x-k。

Example 1
::例1

Divide $\begin{aligned} 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 \end{aligned}$ by $\begin{aligned} x - 2 \end{aligned}$ .
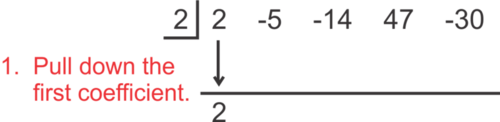
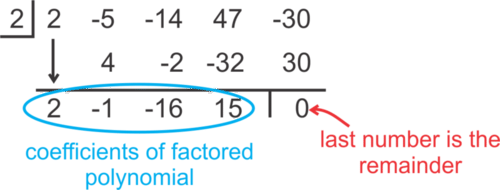
::将 2x4 - 5x3 - 14x2+47x- 30 除以 x-2 。

Solution: To set up the synthetic division, we take the 2 out of the divisor and put it in a box on the left-hand side. Then, we list the coefficients of the dividend next to the box.
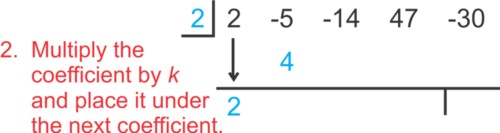
::解决方案: 建立合成师, 我们从断层中取出 2 个, 然后把它放在左手边的盒子里。然后, 在盒子旁边列出红利的系数。

We proceed as follows.
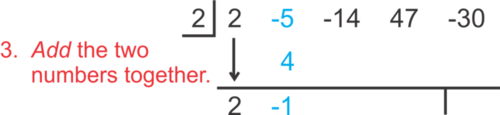
::我们按以下方式进行。

Notice that we changed the sign of the number in the box from -2 to +2. This covers multiplying each of the " terms ," in this case coefficients, of the second polynomial by -1 when we subtract. Now, we are just left with adding.
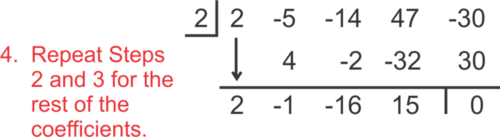
::请注意, 我们将框中数字的符号从 - 2 改为 + 2 。这里覆盖了第二个多数值数的每个“ 条件” 系数乘以 - 1, 当我们减去时。现在, 我们只需添加。

In the last row, the numbers, except for the last number, are the coefficients of the quotient. The last number is the remainder.
::在最后一行,除最后数字外,数字是商数的系数。最后数字是其余。

The quotient is $\begin{aligned} 2 x^{3} - x^{2} - 16 x + 15 \end{aligned}$ . Notice the quotient is one degree less than the dividend because the highest power in $\begin{aligned} x - 2 \end{aligned}$ is 1. Since the last number is 0, there is no remainder. We could also express t his using the Euclidean Division algorithm. To use this form we write the divisor multiplied by the quotient plus the remainder equals the dividend. In this example we have: $\begin{aligned} 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 = (x - 2) (2 x^{3} - x^{2} - 16 x + 15) \end{aligned}$ .
::商数为 2x3 - x2 - 16x+15 。注意商数比股息少一度, 因为x-2 中最高功率为 1 。由于最后数字为 0, 我们没有剩余。我们还可以用 ELCLIDE 算法来表达这一点。要使用此格式, 我们用位数乘以 divisor 乘以数 + 剩余数等于股息。例如, 我们拥有 2x4 - 5x3 - 14x2+47x- 30 = (x-2) (2x3 - x2 - 16x+15) 。

Example 2
::例2

Determine if $\begin{aligned} x - 4 \end{aligned}$ is a factor of $\begin{aligned} f (x) = 5 x^{3} + 6 x^{2} - 24 x - 16 \end{aligned}$ .
::确定 x- 4 是 f( x) = 5x3+6x2 - 24x- 16 的系数。

Solution: $\begin{aligned} x - 4 \end{aligned}$ will be a factor if the remainder equals zero , so we use synthetic division:
::溶液: x-4 将是一个系数, 如果余数等于零, 我们使用合成分解 :

The remainder is 304, so $\begin{aligned} x - 4 \end{aligned}$ is not a factor.
::其余为304,所以x-4不是一个因素。

by Randy Anderson demonstrates how to perform synthetic division.
::Randy Anderson教授如何进行合成分解。

Example 3
::例3

Divide $\begin{aligned} x^{3} + 9 x^{2} + 12 x - 27 \end{aligned}$ by $\begin{aligned} x + 3 \end{aligned}$ .
::x3+9x2+12x-27除以 x3+3。

Solution: We need to change the sign of the number for the box, so instead of 3, we put -3 in the box.
::解答:我们需要更改盒子的号码符号, 所以不是3,而是在盒子里放 -3。

The result is $\begin{aligned} x^{2} + 6 x - 6 - \frac{9}{x + 3} \end{aligned}$ .
::结果是 x2+6x-6-9x+3。

WARNING
::警告

There are a couple of common errors when performing synthetic division.
::在进行合成分解时,有一些常见错误。

1. Make sure to change the sign of the number in the box. In general, if the divisor is $\begin{aligned} x - k \end{aligned}$ , then the number in the box is k . If the divisor is $\begin{aligned} x + k \end{aligned}$ , then the divisor is -k .
::1. 确保更改框中的数字符号。一般而言,如果 divisor is x-k,则框中的数字是 k。如果 divisor is x+k,则divisor is -k。

2. It seems odd that a process where we are dividing involves multiplication and addition . Be careful not to subtract the columns, instead of adding them.
::2. 似乎奇怪的是,我们划分的过程涉及乘数和加法,要小心不要减去栏,而不是增加栏目。

We can also use synthetic division to divide by factors of the form $\begin{aligned} l x - k \end{aligned}$ , where l is an integer , as we see in the next example.
::我们还可以利用合成的分解法,除以表lx-k(I是整数)等因数,我们从下一个例子中可以看到这一点。

Example 4
::例4

Determine if $\begin{aligned} 2 x - 5 \end{aligned}$ is a factor of $\begin{aligned} 4 x^{4} - 9 x^{2} - 100 \end{aligned}$ .
::确定 2x - 5 是 4x4 - 9x2 - 100 的因数。

Solution: Here, we need to figure out what number to put in the box and we do that by setting the divisor equal to zero: $\begin{aligned} 2 x - 5 = 0 \end{aligned}$ . After solving, we see we need to put $\begin{aligned} \frac{5}{2} \end{aligned}$ in the box. Also, there is not a term for every degree less than 4 in this polynomial. We add zero placeholders for the x ³ -term and the x- term.
::解答:在这里,我们需要弄清楚在盒子里放多少个数字, 我们这样做的方法是将断层设为零: 2x- 5=0。解决后, 我们可以看到我们需要在盒子里放52个。另外, 在这个多位数中, 每个字的值不小于 4。我们为 x3 期和 x 期添加零占位符。

The remainder equals zero. This means that $\begin{aligned} 2 x - 5 \end{aligned}$ is a factor.
::其余等于零,这意味着2x-5是一个系数。

by CK-12 demonstrates how to perform synthetic division.
::CK-12表明如何进行合成分解。

Example 5
::例5

Divide $\begin{aligned} 2 x^{4} - 11 x^{3} + 12 x^{2} + 9 x - 2 \end{aligned}$ by $\begin{aligned} 2 x + 1 \end{aligned}$ .
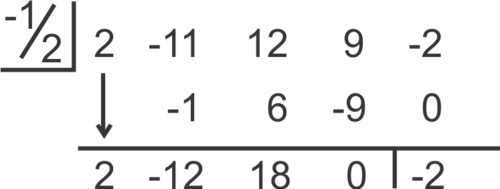
::2x4-11x3+12x2+9x-2除以 2x+1。

Solution: Using synthetic division, divide by $\begin{aligned} - \frac{1}{2} \end{aligned}$ .
::解决办法:使用合成分解法,除以-12。

The result is $\begin{aligned} 2 x^{3} - 12 x^{2} + 18 x - \frac{2}{2 x + 1} \end{aligned}$ .
::结果为 2x3- 12x2+18x- 22x+1。

Summary
::摘要

To divide polynomials when the divisor is of the form $\begin{aligned} l x - k \end{aligned}$ , determine the number to put in the box, list the coefficients of the dividend, pull down the first coefficient, multiply that number with the number in the box, put the result in the next column and add the numbers in the column. Repeat this process until there are no columns remaining.
::要在以 lx- k 格式的边框中分隔多数值, 确定要放入框中的数字, 列出红利的系数, 拉下第一个系数, 将该数值乘以框中的数字, 将结果放入下一列, 并在列中添加数字。重复此进程, 直到没有剩余列。

Review
::回顾

Use synthetic division to divide the following polynomials.
::使用合成分裂法来划分下列多面体。

1. $\begin{aligned} (x^{3} + 6 x^{2} + 7 x + 10) \div (x + 2) \end{aligned}$
::1. (x3+6x2+7x+10) (x+2)

2. $\begin{aligned} (4 x^{3} - 15 x^{2} - 120 x - 128) \div (x - 8) \end{aligned}$
::2. (4x3-15x2-120x-128) (x-8)

3. $\begin{aligned} (4 x^{2} - 5) \div (2 x + 1) \end{aligned}$
::3. (4x2-5)(2x+1)

4. $\begin{aligned} (2 x^{4} - 15 x^{3} - 30 x^{2} - 20 x + 42) \div (x + 9) \end{aligned}$
::4. (2x4-15x3-30x2-20x+42)(x+9)

5. $\begin{aligned} (x^{3} - 3 x^{2} - 11 x + 5) \div (x - 5) \end{aligned}$
::5. (x3-3x2-11x+5) (x-5)

6. $\begin{aligned} (3 x^{5} + 4 x^{3} - x - 2) \div (x - 1) \end{aligned}$
::6. (3x5+4x3-x-2)(x-1)

7. $\begin{aligned} (12 x^{3} + 76 x^{2} + 107 x - 20) \div (x + 3) \end{aligned}$
::7. (12x3+76x2+107x-20)(x+3)

8. $\begin{aligned} (x^{3} - 5 x^{2} - 2 x + 10) \div (x + 2) \end{aligned}$
::8. (x3-5x2-2x+10) (x+2)

9. $\begin{aligned} (6 x^{3} - 17 x^{2} + 11 x - 2) \div (x - 4) \end{aligned}$
::9. (6x3-17x2+11x-2)(x-4)

10. $\begin{aligned} (x^{4} + 7 x^{3} + 6 x^{2} - 32 x - 32) \div (x + 4) \end{aligned}$
::10. (x4+7x3+6x2-32-32x-32)(x+4)

Explore More
::探索更多

1. The volume of a rectangular prism is $\begin{aligned} 2 x^{3} + 5 x^{2} - x - 6 \end{aligned}$ . Determine if $\begin{aligned} 2 x + 3 \end{aligned}$ is the length of one of the prism's sides.
::1. 矩形棱晶体积为2x3+5x2-x-6。确定 2x+3 是棱晶面的长度。

2. Now, confirm the Remainder Theorem by using synthetic division.
::2. 现在,通过合成分解确认残余定理。

a. Find $\begin{aligned} f (- 2) \end{aligned}$ if $\begin{aligned} f (x) = 2 x^{4} - 5 x^{3} - 10 x^{2} + 21 x - 4 \end{aligned}$ .
::a. 如果f(x)=2x4-5x3-10x2+21x-4,则查找 f(-2)。

b. Divide $\begin{aligned} 2 x^{4} - 5 x^{3} - 10 x^{2} + 21 x - 4 \end{aligned}$ by $\begin{aligned} x + 2 \end{aligned}$ synthetically. What do you notice?
::b. 将2x4-5x3-10x2+21x-4除以x+2合成。你注意到什么?

3. Find the lead term and the constant term of the quotient when you divide $\begin{aligned} 2 x^{4} + 3 x^{3} - 7 x + 12 \end{aligned}$ by $\begin{aligned} 2 x - 1 \end{aligned}$ .
::3. 在将 2x4+3x3-7x+12 除以 2x-1 时,查找主词和常数。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

References
::参考参考资料

1. "Ruffini's Rule," last edited March 3, 2017, https://en.wikipedia.org/wiki/Ruffini%27s_rule.
::https://en.wikipedia.org/wiki/ruffini%27s_rule.

Section outline

Synthetic Division ::合成司

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

WARNING ::警告

Example 4 ::例4

Example 5 ::例5

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

References ::参考参考资料

Synthetic Division
::合成司

Example 1
::例1

Example 2
::例2

Example 3
::例3

WARNING
::警告

Example 4
::例4

Example 5
::例5

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

References
::参考参考资料