Section: 距离公式 | 12.2 距离公式

Section outline

Ross directed his boat toward the cottage . He had previously sunk two buoy markers in the water near the cottage, and both locations had ample water below to moor the boat. Ross looked at his chart plot, which showed the coordinates for the cottage and the two buoys. He decided to choose the buoy closest to the cottage.
::罗斯将船指向小屋。他以前在小屋附近的水中沉没了两个浮标标记,两个地点都有充足的水可以停泊小船。罗斯查看了他的地图图图,其中显示了小屋和两个浮标的坐标。他决定选择离小屋最近的浮标。

How can Ross use the coordinates from the chart plot to figure out which buoy is closest to the cottage? In this section, we will discuss how to find distances in two-dimensional space, which is important for conic sections because many definitions for conic sections are in terms of distance in the coordinate plane .
::罗斯如何使用图表图中的坐标来确定哪个浮标离小屋最近?在本节中,我们将讨论如何在两维空间找到距离,这对二次空间很重要,因为对二次空间的二次空间有许多关于二次空间的定义是坐标平面的距离。

Distance in the Coordinate Plane
::坐标平面的距离

Previously, we have discussed how to find distance in one-dimensional space by finding the absolute value of the difference between the two coordinates. Say we want to find the distance between 20 and 5 on a number line. Then, we could find $\begin{aligned} | 20 - 5 | = | 15 | = 15 \end{aligned}$ . They are 15 units apart.
::之前,我们讨论过如何在一维空间找到距离, 找到两个坐标之间的绝对值。说我们要在数字线上找到20到5之间的距离。然后, 我们就可以找到 20 - 5\\\\\\\\\\\\\\\\\\15。它们是15个单元。

In two dimensions , this process gets more complicated. We have to consider the changes in both the $\begin{aligned} x \end{aligned}$ -values and $\begin{aligned} y \end{aligned}$ -values. But how to relate the two? We use a relationship from geometry to help us.
::在两个层面,这一过程变得更加复杂。我们必须考虑 X 值和 y 值的变化。但是如何将两者联系起来? 我们用几何关系来帮助我们。

The graph below shows an orange line that represents the distance between a pet store (1, 6) and a drugstore (8, 2). The green dot on the grid represents Tim's original position. Tim needs to go to both stores. He decides the pet store is closer, so he goes there 1st. He exits the pet store and tries to decide whether to go back to his original position and then to the drugstore, or to walk diagonally to the drugstore. Which way would be the shorter of the two distances if each side of a box represents 10 yards?
::下图显示了一条橙色线,它代表宠物商店(1、6)和药店(8、2)之间的距离。网格上的绿色点代表蒂姆的最初位置。蒂姆需要去两家商店。他决定宠物商店更近, 所以他去第一商店。他从宠物商店出来, 试图决定是否回到原来的位置, 然后回到药店, 或者去对角的药店。如果盒子的两边代表10码, 哪种方式会更短于两条距离的距离?

On the grid, the distance between Tim's original position and the pet store is 4 units, or 40 yards, and the distance between Tim's original position and the drugstore is 7 units, or 70 yards. Together, that path would be 11 units, or 110 yards. We can find these distances because each path is parallel to an axis or number line, so we just use the method for finding the distance on one number line.
::在网格上,蒂姆最初的位置和宠物商店之间的距离是4个单位,或40码,蒂姆最初的位置和药店之间的距离是7个单位,或70码。共同,这条路径将是11个单位,或110码。我们可以找到这些距离,因为每个路径都与轴线或数字线平行,所以我们只是用这个方法来寻找一个数字线上的距离。

To find the length of the diagonal path, notice that the three lines form a right triangle. To find the lengths of the sides, or the distance covered, we can use the Pythagorean Theorem . Here, the path from the pet store to the drugstore is the hypotenuse of the right triangle.
::要找到对角路径的长度, 请注意三条线构成右三角。要找到边的长度或距离, 我们可以使用 Pythagoren Theorem 。这里, 从宠物商店到药店的路径是右三角的下限。

According to the Pythagorean Theorem, we have
::根据毕达哥里安神论,我们有

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ c^{2} & = & 4^{2} + 7^{2} \\ c^{2} & = & 16 + 49 \\ c^{2} & = & 65 \\ \sqrt{c^{2}} & = & \sqrt{65} \\ c & = & 8.06 \end{array} \end{aligned}$

::c2=a2+b2c2=42+72c2=16+49c2=65c2=65c=8.06

The distance is 8.06 units, or 80.6 yards.
::距离是8.06单位,或80.6码

Instead of having to plot the points and draw a right triangle every time we need to find a distance, we can generalize this process. Let's consider two points, $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ . The distance between the $\begin{aligned} x \end{aligned}$ -coordinates is $\begin{aligned} a = | x_{2} - x_{1} |, \end{aligned}$ since we are finding the distance parallel to the $\begin{aligned} x \end{aligned}$ -axis or number line. Similarly, the distance between the $\begin{aligned} y \end{aligned}$ -coordinates is $\begin{aligned} b = | y_{2} - y_{1} | \end{aligned}$ .
::与其每次需要找到距离时绘制点和绘制右三角形,不如将这个过程概括化。让我们考虑两个点,即(x1,y1)和(x2,y2),x坐标之间的距离是ax2-x1,因为我们正在找到与x轴或数字线平行的距离。同样,y坐标之间的距离是b2-y1。

Plugging these into the Pythagorean Theorem, we have
::把这些塞进毕达哥里安神论中

$\begin{aligned} c^{2} & = a^{2} + b^{2} \\ c^{2} & = (| x_{2} - x_{1} |)^{2} + (| y_{2} - y_{1} |)^{2} \\ c^{2} & = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} & absolute value redundant since squaring \\ c & = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$

::c2=a2+b2c2=(x2-x1)2+(y2-y1)2+(y2-y1)2c2=(x2-x1)2+(y2-y1)2+(y2-y1)2+(y2-y1)2 冗余绝对值,因为正弦环 c=(x2-x1)2+(y2-y1)2

Since we are finding distance, we use $\begin{aligned} d \end{aligned}$ instead of $\begin{aligned} c \end{aligned}$ .
::既然我们找到了距离我们用d而不是c

Distance Formula
::距离公式

The distance, $\begin{aligned} d \end{aligned}$ , between two points $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ is
::两个点(x1,y1)和(x2,y2)之间的距离(d)是

$\begin{aligned} d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2

Let's apply this formula to find the distance between the pet store and the drugstore. Remember, the coordinates of the pet store were (1, 6) and those of the drugstore were (8, 2).
::请记住,宠物商店的座标是(1,6),药店的座标是(8,2)。

First, let's label the 1st and 2nd points. The distance will be the same regardless of how the points are chosen. This is helpful to match the correct value with its corresponding variable .
::首先, 让我们给第一和第二点贴上标签。无论选择的点如何, 距离都是一样的。这有助于将正确的值与其相应的变量匹配。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 1, & 6 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 8, & 2 \end{matrix}) \end{aligned}$

:x1,y11,6)和(x2,y28,2)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(8 - 1)^{2} + (2 - 6)^{2}} \\ d & = & \sqrt{7^{2} + (- 4)^{2}} \\ d & = & \sqrt{49 + 16} \\ d & = & \sqrt{65} \\ d & = & 8.06 \end{array} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(8-1)2+(2-6)2d=72+(4)2d=49+16d=65d=8.06

The distance is 8.06 units, or 80.6 yards.
::距离是8.06单位,或80.6码

by Mathispower4u shows how to find the distance formula using the Pythagorean Theorem and offers some examples.
::由 Mathispower4u 展示如何使用毕达哥里安理论来找到距离公式, 并举一些例子。

Example 1
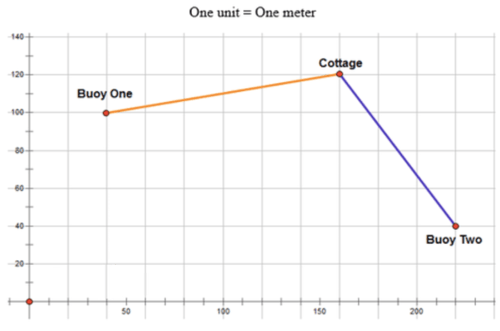
::例1

Ross uses the chart below to figure out which buoy is closer to the cottage, so he can moor his boat. Find which buoy is closer.
::罗斯用下面的图表找出哪个浮标离小屋更近所以他可以停泊船

Solution: First, write the coordinates for each distance to be calculated, and then use the distance formula.
::解答: 首先, 写出每个要计算距离的坐标, 然后使用距离公式。

$\begin{aligned} \begin{array}{rcl} Cottage to Buoy One & Cottage to Buoy Two \\ (160, 120) and (40, 100) & (160, 120) and (220, 40) \end{array} \end{aligned}$

::Buy OneCottage to Buoy Two(160,120)和(40,100(160,120)和(220,40))

Distance from cottage to Buoy One:
::从小屋到 Buy One 的距离:

First, we label
::首先,我们标签

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 160, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 40, & 100 \end{matrix}) . \end{aligned}$

:x1,y1160,120)和(x2,y240,100)。

Next, we write the distance formula and substitute the values for the variables.
::接下来,我们写出距离公式, 并替换变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(40 - 160)^{2} + (100 - 120)^{2}} \\ d & = & \sqrt{(- 120)^{2} + (- 20)^{2}} \\ d & = & \sqrt{14, 400 + 400} \\ d & = & \sqrt{14, 800} \\ d & = & 121.66 \end{array} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(40-160)2+(100-120)2d=(-120)2+(-20)2d=14,400+400d=14,800d=121.66

The distance from the cottage to Buoy One is 121.66 meters.
::从小屋到Buoy One的距离是121.66米

Distance from cottage to Buoy Two:
::从小屋到布瓦二号的距离:

First, la bel t he 1st and 2nd points.
::首先,给第一和第二点贴上标签。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 160, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 220, & 40 \end{matrix}) \end{aligned}$

:x 1,y1160,120)和(x2,y2220,40)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(220 - 160)^{2} + (40 - 120)^{2}} \\ d & = & \sqrt{60^{2} + (- 80)^{2}} \\ d & = & \sqrt{3, 600 + 6, 400} \\ d & = & \sqrt{10, 000} \\ d & = & 100 \end{array} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(220-160)2+(40-120)2d=602+(-80)2d=3 600+6 400d=10 000d=100

The distance from the cottage to Buoy Two is 100 meters. Ross will moor the boat at Buoy Two.
::从小屋到布伊二号的距离是100米罗斯会把船停在布伊二号

Example 2
::例2

Use the distance formula to find the distance between these points to the nearest tenth: $\begin{aligned} A (54, 120) \end{aligned}$ and $\begin{aligned} B (113, 215) \end{aligned}$ .
::使用距离公式查找这些点与最近的十分点之间的距离:A(54,120)和B(113,215)。

Solution: Assigning point 1 and point 2 to these points, and then substituting in the formula, we have:
::解决方案:将第1点和第2点指定为这些点,然后在公式中取代,我们有:

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 54, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 113, & 215 \end{matrix}) \end{aligned}$

:x1,y154,120)和(x2,y2113,215)

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(113 - 54)^{2} + (215 - 120)^{2}} \\ d & = & \sqrt{59^{2} + 95^{2}} \\ d & = & \sqrt{3, 481 + 9, 025} \\ d & = & \sqrt{12, 506} \\ d & = & 111.8 \end{array} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2d=(113-54)2+(215-120)2d=592+952d=3 481+9,025d=12,506d=111.8

Example 3
::例3

Use the distance formula to find the distance between the points $\begin{aligned} D (3, - 4) \end{aligned}$ and $\begin{aligned} E (- 2, - 10) \end{aligned}$ .
::使用距离公式查找点D(3,4)和点E(2,2,10)之间的距离。

Solution:
::解决方案 :

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 3, & - 4 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ - 2, & - 10 \end{matrix}) \\ \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(- 2 - 3)^{2} + (- 10 - (- 4))^{2}} \\ d & = & \sqrt{(- 5)^{2} + (- 6)^{2}} \\ d & = & \sqrt{25 + 36} \\ d & = & \sqrt{61} \\ d & = & 7.8 \end{array} \end{aligned}$

:x1,y13,4)和(x2,y2-2,10)d=(x2,y2-2,10)d=(x2,y2-x1)2+(y2-y1)2d=(-2-3)2+(---(-4))2+(-)2d=(-5)2+(-6)2d=25+36d=61d=7.8)

The distance from $\begin{aligned} D \end{aligned}$ to $\begin{aligned} E \end{aligned}$ is 7.8 units.
::从D到E的距离是7.8个单位。

by CK-12 shows some examples using the Pythagorean Theorem .
::以 CK-12 显示一些使用 Pythagorena 理论的例子。

Example 4
::例4

The following circle has its center at the point (5, 3) and a radius of 3 inches. Use the distance formula to determine if the point (8, 5) is inside the circle, on the circle, or outside the circle.
::以下圆的中点为5、3和半径为3英寸。使用距离公式确定点(8、5)在圆内、圆上或圆外。

Solution: We use the distance formula to find the distance between the center of the circle (5, 3) and the point (8, 5).
::解答:我们使用距离公式来找到圆的中心(5,3)和点(8,5)之间的距离。

First, label the 1st and 2nd points.
::首先,给第一和第二点贴上标签。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 5, & 3 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 8, & 5 \end{matrix}) \end{aligned}$

:x1,y15,3)和(x2,y28,5)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(8 - 5)^{2} + (5 - 3)^{2}} \\ d & = & \sqrt{3^{2} + 2^{2}} \\ d & = & \sqrt{9 + 4} \\ d & = & \sqrt{13} \\ d & = & 3.6 \end{array} \end{aligned}$

::d=(x2-x1)2+(y2-y1)2d=(8-5)2+(5-3)2d=32+22d=9+4d=13d=3.6)

The distance from the center of the circle to the point (8, 5) is 3.6 inches. The point will be outside the circle, since this distance is greater than the length of the radius.
::从圆的中心到点(8,5)的距离是3.6英寸。点在圆外, 因为距离大于半径的长度。

Feature: It All Depends on Distance
::特点:全部取决于距离

by Jen Kershaw
::由Jen Kershaw著

Have you ever needed to know the location of a river, lake, or range of mountains? How about a glacier or a wetland? Or perhaps a patch of hazardous waste?
::你是否需要知道河流、湖泊或山脉的位置?冰川或湿地如何?或许是一片危险废物?

Why It Matters
::为何重要

If you were interested in locating any of those things, you'd have needed to rely on the work of a land surveyor. Surveying is a highly mathematical profession that takes you outdoors and requires a great deal of skill. It is a job that is needed in both rural and urban settings. Depending on your interests, you could become a surveyor for some of the most remote places in the world, or work right in your own neighborhood.
::如果您有兴趣找到其中的任何事物, 您需要依赖土地测量师的工作。测量是一种高度数学的职业, 需要你到户外, 需要大量技能。这是在农村和城市环境中都需要的工作。取决于您的利益, 您可以成为世界上某些最偏远地方的测量师, 或者在自己的社区工作。

Surveyors have the task of accurately measuring land in order to plot exact locations or find the distances between certain points. To do so, they use surveying equipment, information from satellites, and aerial photographs taken from planes. It's all about math! To be a surveyor, you must have a thorough knowledge of maps, contour lines, and geometry.
::测量员的任务是精确测量土地, 以便绘制准确的位置或找到某些点之间的距离。为此, 他们使用测量设备、卫星信息, 以及飞机拍摄的航空照片。这都是关于数学的。要成为测量员, 您必须完全了解地图、轮廓线和几何学。

Surveyors are in high demand. Governments and private industries need surveyors to chart, measure, and plot out features of land, ranging from a boundary line for a city project, to the location of a natural resource, like a hot spring or waterfall. Either way, being able to calculate the distance between two points is a must!
::测量者的需求很高。政府和私营企业需要测量者绘制、测量和绘制土地特征,从城市项目的边界线到自然资源的位置,如温泉或瀑布。无论哪种方式,能够计算两点之间的距离都是必须的!

by CityofBloomingtonMN shows how the process of surveying works.
::CityofBloomingtonMN展示了勘测过程如何运作。

Summary
::摘要

The distance, $\begin{aligned} d \end{aligned}$ , between two points in the coordinate plane, $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ , can be found using the formula $\begin{aligned} d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} . \end{aligned}$
::坐标平面中两个点(x1,y1)和(x2,y2)之间的距离(d),可用公式d=(x2-x1)2+(y2-y1)2找到。

Review
::回顾

Use the distance formula to find the distance between the pairs of points below. You may round to the nearest tenth when necessary.
::使用距离公式来查找以下两对点之间的距离。必要时您可以圆到最近的十点。

1. What is the distance between (3, 6) and (-1, 3)?
::1. (3,6)和(-1,3)之间的距离是多少?

2. What is the distance between (-2,-2) and (10, 3)?
::2. (2-2)和(10,3)之间的距离是多少?

3. What is the distance between (1,9) and (9,1)?
::3. (1,9)和(9,1)之间的距离是多少?

4. What is the distance between (-5,-5) and (-2,-1)?
::4. (5-5)和(2-1)之间的距离是多少?

5. What is the distance between (2, 12) and (3,7)?
::5. (2,12)和(3,7)之间的距离是多少?

6. What is the distance between (2, 2) and (8, 2)?
::6. (2,2)和(8,2)之间的距离是多少?

7. What is the distance between (-3, 4) and (2, 0)?
::7. (3、4)和(2,0)之间的距离是多少?

8. What is the distance between (3, 4) and (3, -4)?
::8. (3,4)和(3,4)之间的距离是多少?

9. What is the distance between (-4, -3) and (1, -1)?
::9. (4-4-3)和(1,-1)之间的距离是多少?

10. What is the distance between (-6, 2) and (-3, 1)?
::10. (-6,2)和(-3,1)之间的距离是多少?

Explore More
::探索更多

Answer each of the following questions using the map of Bryan's town, below .
::使用布赖恩镇的地图回答下面的每一个问题

11. What is the distance between the pet store and the town hall?
::11. 宠物商店和市政厅之间的距离是多少?

12. What is the distance between the pet store and the courthouse?
::12. 宠物商店与法院之间的距离是多少?

13. What is the distance between the courthouse and the library?
::13. 法院与图书馆之间的距离是多少?

14. What is the distance between the library and the town hall?
::14. 图书馆与市政厅之间的距离是多少?

15. What is the distance between the pet store and the library?
::15. 宠物商店与图书馆之间的距离是多少?

Answers to Review and Explore More Problems
::对审查和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try the interactives to reinforce the concepts explored in this section.
::尝试交互式来强化本节所探讨的概念。

Section outline

Distance in the Coordinate Plane ::坐标平面的距离

Distance Formula ::距离公式

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Feature: It All Depends on Distance ::特点:全部取决于距离

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers to Review and Explore More Problems ::对审查和探讨更多问题的答复

PLIX ::PLIX

Distance in the Coordinate Plane
::坐标平面的距离

Distance Formula
::距离公式

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Feature: It All Depends on Distance
::特点:全部取决于距离

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers to Review and Explore More Problems
::对审查和探讨更多问题的答复

PLIX
::PLIX