节: 亚学序列 | 13.3 科研序列

章节大纲

Halley's Comet appears in the sky approximately every 76 years. The comet was first spotted in the year 1531. ¹ Find the n ^th term rule and the $\begin{aligned} 10^{t h} \end{aligned}$ term for the represented by this situation.

A sequence like this is called an arithmetic sequence . We cover this type of sequence in this section.
::像这样的序列被称为算术序列。我们在本节覆盖了这种序列。

Arithmetic Sequences
::亚学序列

An arithmetic sequence is a sequence in which the difference between two consecutive terms is constant. We call this difference the common difference .
::算术序列是连续两个任期之间的差别不变的序列。我们称这一差别为共同差别。

Example 1
::例1

Find the common difference and n ^th term rule for the arithmetic sequence: $\begin{aligned} 2, 5, 8, 11 \dots \end{aligned}$
::找到计算序列的通用差数和 nth 术语规则: 2,5,8,11...

Solution: To find the common difference, we subtract consecutive terms.
::解决方案:为了找到共同的差别,我们将连续减掉。

$\begin{aligned} 5 - 2 & = 3 \\ 8 - 5 & = 3 & the common difference is 3 \\ 11 - 8 & = 3 \end{aligned}$

::5-2=38-5=3 共同差为311-8=3

Now we can use our first term, 2, and common difference, 3, to find the n ^th term rule. The third term is 8 and 8 = 2 + (2 x 3). Similarly, the fourth term is 11 and 11 = 2 + (3 x 3). In general, we can obtain the term by adding 2 (the first term) to the product of 3 (the common difference) and n - 1 (where n is the term). Thus, number we multiply 3 by is one less than the term number. As a formula, that is:
::现在,我们可以用我们的第一个任期,2和共同的差别,3, 来找到第n个任期规则。第三个任期是8和8=2+2(2x3),同样,第四个任期是11和11=2+2(3x3),一般来说,我们可以通过在3(共同差别)和n-1(其中n为术语)的产物中增加2(第一个任期)和n-1(其中n为术语)来获得该术语。因此,我们乘以3乘以1比术语数少一个。作为一个公式,即:

$\begin{aligned} a_{n} & = 2 + (n - 1) (3) \\ = 2 + 3 n - 3 \\ = 3 n - 1. \end{aligned}$

::a=2+(n-1)(3)=2+3n-3=3n-1。

Example 2
::例2

Find the common difference and the n ^th term rule for the sequence: $\begin{aligned} 5, - 3, - 11, \dots \end{aligned}$
::找出共同的区别和Nth术语规则序列: 5 -3 -11,...

Solution: The common difference is $\begin{aligned} - 3 - 5 = - 8 \end{aligned}$ . For the formula, the same idea holds as in example 1—the n ^th term is the 1st term, plus one less than the term number times the common difference.
::解决方案: 常见的差别是 - 3 - 5= 8。对于公式, 与例1中的相同概念是 1 - 第 n 个词是第一个词, 加上一个小于该词数乘以共同差数的词数。

$\begin{aligned} a_{n} & = 5 + (n - 1) (- 8) \\ = 5 - 8 n + 8 \\ = - 8 n + 13 \end{aligned}$

::a=5+(n-1)(-8)=5-8n+8=8n+8=-8n+13

We can generalize a formula for an arithmetic sequence. First, $\begin{aligned} a_{n} - a_{n - 1} = d \end{aligned}$ , where $\begin{aligned} a_{n - 1} \end{aligned}$ and $\begin{aligned} a_{n} \end{aligned}$ represent two consecutive terms, and $\begin{aligned} d \end{aligned}$ represents the common difference. Since the same value, the common difference, $\begin{aligned} d \end{aligned}$ , is added to get each successive term in an arithmetic sequence, we can determine the value of any term from the 1st term and how many times we need to add $\begin{aligned} d \end{aligned}$ to get to the desired term as illustrated below:
::我们可以概括一个计算序列的公式。首先, an- an-1=d, 其中an- 1和代表两个连续任期, d 代表共同的差数。由于相同值, 共同差数 d 被添加到一个算术序列中, 我们可以确定第一个任期中任何任期的值, 以及我们需要增加多少次 d 才能达到下面所述的预期任期:

Let's consider the sequence $\begin{aligned} 22, 19, 16, 13, \dots, \end{aligned}$ in which $\begin{aligned} a_{1} = 22 \end{aligned}$ and $\begin{aligned} d = - 3 \end{aligned}$ .
::让我们来考虑一下顺序22,19,16,13... 其中a1=22和d=3

$\begin{aligned} a_{1} & = 22 o r 22 + (1 - 1) (- 3) = 22 + 0 = 22 \\ a_{2} & = 19 o r 22 + (2 - 1) (- 3) = 22 + (- 3) = 19 \\ a_{3} & = 16 o r 22 + (3 - 1) (- 3) = 22 + (- 6) = 16 \\ a_{4} & = 13 o r 22 + (4 - 1) (- 3) = 22 + (- 9) = 13 \\ ⋮ \\ a_{n} & = 22 + (n - 1) (- 3) \\ a_{n} & = 22 - 3 n + 3 \\ a_{n} & = - 3 n + 25 \end{aligned}$

::a1=22或22+(1-1)(3-3)=22+0=22a2=19或22+(2-1)(3)=22+(3-1)(3)=19a3=16或22+(3-1)(3-1)(3)=22+(6)=16a4=13或22+(4-1)(3)=22+(9)=22+(9)=13+(n-1)(3)=22-3n+3nn+3nn+3n+25

Now we can generalize this into a rule for the n ^th term of any arithmetic sequence.
::现在我们可以把它概括为任何算术序列的第 n 术语的规则。

n ^th Term of Arithmetic Sequence
::nth 亚学序列期数

The n ^th term of an arithmetic sequence is given by
::计算序列的第 n 术语由

$\begin{aligned} a_{n} = a_{1} + (n - 1) d, \end{aligned}$
where $\begin{aligned} a_{1} \end{aligned}$ is the 1st term of the sequence and $\begin{aligned} d \end{aligned}$ is the common difference.
::a=a1+(n-1)d,其中a1是序列的第一个条件,d是共同的区别。

Example 3
::例3

Find the n ^th term rule and thus the $\begin{aligned} 100^{t h} \end{aligned}$ term for the arithmetic sequence in which $\begin{aligned} a_{1} = - 9 \end{aligned}$ and $\begin{aligned} d = 2 \end{aligned}$ .
::查找 nth 术语规则, 从而查找 a1=- 9 和 d= 2 的算术序列的第100个术语。

Solution: We have what we need to substitute into the rule:
::解决:我们有我们需要的替代规则:

$\begin{aligned} a_{n} & = - 9 + (n - 1) (2) \\ = - 9 + 2 n - 2 \\ = 2 n - 11 \end{aligned}$

::a=-9+(n-1)(2)=-9+2n-2n-2=2n-11

Now to find the $\begin{aligned} 100^{t h} \end{aligned}$ term we can use our rule and replace $\begin{aligned} n \end{aligned}$ with 100: $\begin{aligned} a_{100} = 2 (100) - 11 = 200 - 11 = 189 \end{aligned}$ .
::现在找到第100个术语,我们可以使用我们的规则,用100:a=2(100)-11=200-11=189取代n。

Example 4
::例4

Halley's Comet appears in the sky approximately every 76 years. The comet was first spotted in the year 1531. Find the n ^th term rule and the 10th term for the sequence represented by this situation.
::Halley的彗星大约每隔76年出现在天空中一次。彗星是1531年首次发现的。找到以这种情形为代表的顺序的第 n 学期规则和第 10 学期。

Solution: From the information given, we can conclude that $\begin{aligned} a_{1} = 1, 531 \end{aligned}$ and $\begin{aligned} d = 76 \end{aligned}$ .
::解决办法:根据所提供的信息,我们可以得出a1=1,531和d=76。

We now have what we need to substitute into the rule:
::我们现在有需要替代的规则:

$\begin{aligned} a_{n} & = 1, 531 + (n - 1) (76) \\ = 1, 531 + 76 n - 76 \\ = 76 n + 1, 455 \end{aligned}$

::a=1,531+(n-1)(76)=1,531+76n=76n+1,455

Now, to find the $\begin{aligned} 10^{t h} \end{aligned}$ term we can use our rule and replace $\begin{aligned} n \end{aligned}$ with 10: $\begin{aligned} a_{10} = 76 (10) + 1, 455 = 760 + 1, 455 = 2, 215. \end{aligned}$
::现在,为了找到第10个术语,我们可以使用我们的规则,用10:a10=76(10)+1,455=760+1,455=2,215取代n。

by Mathispower4u shows several examples of arithmetic sequences.
::由 Mathispower4u 表示数个算术序列的例子。

Example 5
::例5

Write the n ^th term rule and find the $\begin{aligned} 45^{t h} \end{aligned}$ term for the arithmetic sequence with $\begin{aligned} a_{10} = 1 \end{aligned}$ and $\begin{aligned} d = - 6 \end{aligned}$ .
::以 a10=1 和 d=6 来写入 nth 术语规则, 并找到算术序列的第 45 个术语。

Solution: To find the 1st term:
::解决方案:找到第一个术语:

$\begin{aligned} a_{1} + (10 - 1) (- 6) & = 1 \\ a_{1} - 54 & = 1 \\ a_{1} & = 55 \end{aligned}$

::a1+(10-1)(-6)=1a1-54=1a1=55

Find the n ^th term rule: $\begin{aligned} a_{n} = 55 + (n - 1) (- 6) = 55 - 6 n + 6 = - 6 n + 61 \end{aligned}$ .
::查找 nth 术语规则: an=55+(n- 1)(-6)=55- 6n+6=-6n+61。

Finally, the $\begin{aligned} 45^{t h} \end{aligned}$ term: $\begin{aligned} a_{45} = - 6 (45) + 61 = - 209 \end{aligned}$ .
::最后,第45个学期:a45=6(45)+61=209。

Example 6
::例6

Find the common difference, 1st term, and n ^th term rule for the arithmetic sequence in which $\begin{aligned} a_{7} = 17 \end{aligned}$ and $\begin{aligned} a_{20} = 82 \end{aligned}$ .
::查找 7 = 17 和 a20= 82 的算术序列的常见差数, 第一个术语和 nth 术语规则。

Solution: We will start by using the n ^th term rule for an arithmetic sequence to create two equations in two variables:
::解答: 我们首先使用 nth 术语规则来计算一个算术序列, 在两个变量中创建两个方程式 :

$\begin{aligned} a_{7} & = 17 & a_{20} = 82 \\ a_{1} + (7 - 1) d & = 17 & a_{1} + (20 - 1) d = 82 \\ a_{1} + 6 d & = 17 & a_{1} + 19 d = 82 \end{aligned}$

::a7=17a20=82a1+(7-1)d=17a1+(20-1)d=82a1+6d=17a1+19d=82

Solve the resulting system:
::解决产生的系统 :

$\begin{aligned} a_{1} + 6 d = 17 a_{1} + 6 d = 17 \\ \underline{- 1 (a_{1} + 19 d = 82)} \Rightarrow \underline{- a_{1} - 19 d = - 82} \\ - 13 d = - 65 \\ d = 5 \end{aligned}$

::a1+6d=17a1+6d=17-1(a1+19d=82) @a1-19d=-82_-13d=-65d=5

Now, replacing $\begin{aligned} d \end{aligned}$ with 5 in one of the equations we get
$\begin{aligned} a_{1} + 6 (5) & = 17 \\ a_{1} + 30 & = 17 \\ a_{1} & = - 13. \end{aligned}$

::现在,将 d 替换为 5 方程式中的一个方程式, 我们得到 a1+6(5)=17a1+30=17a1=13。

Using these values we can find the n ^th term rule:
::使用这些价值,我们可以找到nth术语规则:

$\begin{aligned} a_{n} & = - 13 + (n - 1) (5) \\ a_{n} & = - 13 + 5 n - 5 \\ a_{n} & = 5 n - 18. \end{aligned}$

::a=-13+(n-1)(5)an=-13+5n-5an=5n-18。

by CK-12 demonstrates how to find the n ^th term rule given two terms.
::CK-12 显示如何在两个任期中找到 nth 术语规则。

Example 7
::例7

Find the common difference, 1st term, and n ^th term rule for the arithmetic sequence in which $\begin{aligned} a_{11} = - 13 \end{aligned}$ and $\begin{aligned} a_{40} = - 71 \end{aligned}$ .
::为a11=-13和a40=-71的算术序列查找共同的差数,第一个术语和nth术语规则。

Solution: Though this is the same question as the previous example, we are going to use a different approach. The n ^th term rule uses the 1st term and adds $\begin{aligned} d \end{aligned}$ to it $\begin{aligned} n - 1 \end{aligned}$ times to find the n ^th term. We are going to use this idea to find the common difference. To get from the $\begin{aligned} 11^{t h} \end{aligned}$ term to the $\begin{aligned} 40^{t h} \end{aligned}$ term, the common difference is added $\begin{aligned} 40 - 11 \end{aligned}$ or $\begin{aligned} 29 \end{aligned}$ times. The difference in the term values is $\begin{aligned} - 71 - (- 13) \end{aligned}$ or $\begin{aligned} - 58 \end{aligned}$ . What must be added $\begin{aligned} 29 \end{aligned}$ times to create a difference of $\begin{aligned} - 58 \end{aligned}$ ? We can subtract the terms and divide by the difference in term number to determine the common difference.
::解答: 虽然这是与前一个例子相同的问题, 我们将会使用不同的方法。第n 术语规则使用第一个术语, 并给它添加 d- 1 次来查找 n- 1 次。我们将使用这个概念来找到共同的差别。从第 11 个术语到第 40 个术语, 共同的差别会增加 40- 11 或 29 次。术语值的差别是 - 71- (- 13) 或 - 58 。要产生 - 58 的差别, 需要增加 29 次 ? 我们可以用术语和数字的差别来减去。

$\begin{aligned} \frac{- 71 - (- 13)}{40 - 11} = \frac{- 71 + 13}{29} = \frac{- 58}{29} = - 2 \end{aligned}$

So $\begin{aligned} d = - 2 \end{aligned}$ . Now we can use the common difference and one of the terms to find the 1st term as we did previously.
::所以d=-2。现在我们可以使用共同的区别和其中的一个术语来找到我们之前的第一个术语。

$\begin{aligned} a_{1} + (11 - 1) (- 2) & = - 13 \\ a_{1} + (- 20) & = - 13 \\ a_{1} & = 7 \end{aligned}$

::a1+(11-1)(-2)=-13a1+(-20)=-13a1=7

Writing the n ^th term rule, we get $\begin{aligned} a_{n} = 7 + (n - 1) (- 2) = 7 - 2 n + 2 = - 2 n + 9 \end{aligned}$ .
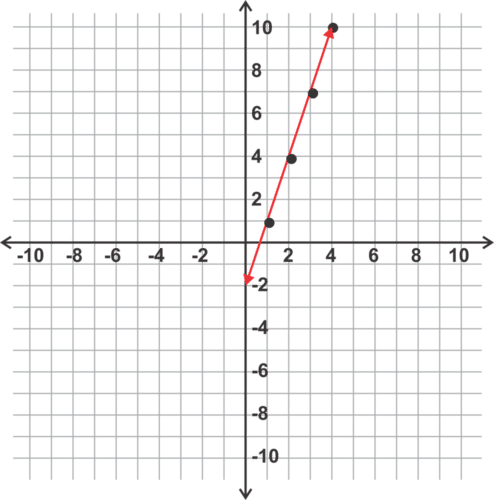
::写入 nth 术语规则时, 我们得到 an=7+(n- 1)(-2)=7- 2n+2=-2n+9。

Notice that the simplified n ^th term rule, $\begin{aligned} a_{n} = p n + q \end{aligned}$ , where $\begin{aligned} p \end{aligned}$ and $\begin{aligned} q \end{aligned}$ represent constants, looks a little like $\begin{aligned} y = m x + b \end{aligned}$ , the slope-intercept form of the equation of a line. Let's explore why this is the case using the arithmetic sequence $\begin{aligned} 1, 4, 7, 10, \dots \end{aligned}$ If we create points by letting the x -coordinate be the term number and the y -coordinate be the term, we get the following points and can plot them in the coordinate plane as shown below:
::注意简化 nth 术语规则, an=pn+q, 其中 p和 q 代表常数, 看上去有点像 y=mx+b, 线形方程的斜度拦截形式。让我们来探讨为什么使用算术序列 1, 4, 7, 10,... 如果我们通过让 x 坐标为术语编号而创建点, y 坐标为术语, 我们得到以下点, 并可以在坐标平面上绘制如下 :

The points are $\begin{aligned} (1, 1), (2, 4), (3, 7), (4, 10) . \end{aligned}$
::要点是(1,1),(2,4),(3,7),(4,10)。

Notice that all these points lie on the same line. This happens because for each increase of 1 in the term number $\begin{aligned} (x) \end{aligned}$ , the term value "> $\begin{aligned} (y) \end{aligned}$ increases by 3. This common difference is actually the slope of the line.
::注意所有这些点都位于同一行。这是因为每增加1个( x), 术语值增加3个。这个共同差实际上是线的斜坡。

We can find the equation of this line using the slope, 3, and the point $\begin{aligned} (1, 1) \end{aligned}$ in the equation $\begin{aligned} y = m x + b \end{aligned}$ as follows:
::在y=mx+b的方程式中,用斜度3和点(1,1)来找到这条线的方程式如下:

$\begin{aligned} 1 & = 3 (1) + b \\ 1 & = 3 + b & the equation of the line is y = 3 x - 2 \\ - 2 & = b \end{aligned}$

::1=3(1)+b1=3+bb 行的方程式是y=3x-2=b

The n ^th term rule for the sequence is thus $\begin{aligned} a_{n} = 3 n - 2 \end{aligned}$ .
::因此,序列的 nth 术语规则为 an= 3n-2 。

Example 8
::例8

Find the common difference, 1st term, and n ^th term rule for the arithmetic sequence in which $\begin{aligned} a_{10} = - 50 \end{aligned}$ and $\begin{aligned} a_{32} = - 182 \end{aligned}$ .
::为a10=-50和a32=-182的算术序列查找共同的差数,第一个术语和nth术语规则。

Solution: This time we will use the concept that the terms in an arithmetic sequence are actually points on a line to write an equation. Here our points are $\begin{aligned} (10, - 50) \end{aligned}$ and $\begin{aligned} (32, - 182) \end{aligned}$ . We can find the slope and the equation as shown.
::解答: 这次我们将使用一个概念, 算术序列中的术语实际上是线上的点来写一个公式。这里的点是( 10, 50) 和( 32, 182) 。我们可以找到斜度和方程。

$\begin{aligned} m = \frac{- 182 - (- 50)}{32 - 10} = \frac{- 132}{22} = - 6 \end{aligned}$

::m=-182-(-5032-10=-13222=-6)

Use the point $\begin{aligned} (10, - 50) \end{aligned}$ to find the $\begin{aligned} y \end{aligned}$ -intercept:
$\begin{aligned} - 50 & = - 6 (10) + b \\ - 50 & = - 60 + b \\ 10 & = b \end{aligned}$
So $\begin{aligned} y = - 6 x + 10 \end{aligned}$ and $\begin{aligned} a_{n} = - 6 n + 10 \end{aligned}$ .
::使用点 (10,-50) 来查找 Y 界面 : - 50=-6(10)+b- 50=- 60+b10=bSo y6x+10 和 an=-6n+10 。

Summary
::摘要

An arithmetic sequence is a sequence in which the difference between two consecutive terms is constant. We call this difference the common difference.
::算术序列是连续两个任期之间的差别不变的序列。我们称这一差别为共同差别。

The formula for an arithmetic sequence is $\begin{aligned} a_{n} = a_{1} + (n - 1) d \end{aligned}$ .
::算术序列的公式为 an=a1+(n-1)d。

Review
::回顾

Identify which of the sequences below is arithmetic. If the sequence is arithmetic, find the $\begin{aligned} n^{t h} \end{aligned}$ term rule.
::下面的顺序是算术。如果序列是算术,请找到 nth 术语规则。

1. $\begin{aligned} 2, 3, 4, 5, \dots \end{aligned}$

2. $\begin{aligned} 6, 2, - 1, - 3, \dots \end{aligned}$

3. $\begin{aligned} 5, 0, - 5, - 10, \dots \end{aligned}$

4. $\begin{aligned} 1, 2, 4, 8, \dots \end{aligned}$

5. $\begin{aligned} 0, 3, 6, 9, \dots \end{aligned}$

6. $\begin{aligned} 13, 12, 11, 10, \dots \end{aligned}$

7. $\begin{aligned} 4, - 3, 2, - 1, \dots \end{aligned}$

8. $\begin{aligned} a, a + 2, a + 4, a + 6, \dots \end{aligned}$
::8. a, a+2, a+4, a+6,...

Write the n ^th term rule for each arithmetic sequence with the given term and common difference.
::以给定的术语和常见差数为每个算术序列写入 nth 术语规则。

9. $\begin{aligned} a_{1} = 15 \end{aligned}$ and $\begin{aligned} d = - 8 \end{aligned}$
::9.1=15和d=8

10. $\begin{aligned} a_{1} = - 10 \end{aligned}$ and $\begin{aligned} d = \frac{1}{2} \end{aligned}$
::10.1=-10和d=12

11. $\begin{aligned} a_{3} = 24 \end{aligned}$ and $\begin{aligned} d = - 2 \end{aligned}$
::11.3=24和d=-2

12. $\begin{aligned} a_{5} = - 3 \end{aligned}$ and $\begin{aligned} d = 3 \end{aligned}$
::12.5=-3和d=3

13. $\begin{aligned} a_{10} = - 15 \end{aligned}$ and $\begin{aligned} d = - 11 \end{aligned}$
::13.a10=-15和d=-11

14. $\begin{aligned} a_{7} = 32 \end{aligned}$ and $\begin{aligned} d = 7 \end{aligned}$
::14.7=32和d=7

15. $\begin{aligned} a_{n - 2} = 3 n + 2 \end{aligned}$ , find $\begin{aligned} a_{n} \end{aligned}$
::15. an-2=3n+2, 找到a

Explore More
::探索更多

1. You are paying off a student loan in monthly installments. After your 5th payment, your remaining balance on the loan is $17,500. After your $\begin{aligned} 16 t h \end{aligned}$ payment, your remaining balance is $12,000. What is the $\begin{aligned} n^{t h} \end{aligned}$ term rule for the sequence represented by this situation?
::1. 每月分期偿还学生贷款,第五个分期偿还后,贷款余额为17 500美元,第16个分期偿还后,余额为12 000美元。

2. A sequence is harmonic if the reciprocals of the terms form an arithmetic sequence. Determine whether the following sequences are harmonic:
::2. 如果术语的对等构成一个算术序列,则一个序列即为调和。

a. $\begin{aligned} 1, \frac{1}{4}, \frac{1}{7}, \frac{1}{10}, \frac{1}{13}, . . . \end{aligned}$
::a. 1,14,17,110,113,...

b. $\begin{aligned} 2, \frac{3}{2}, \frac{6}{5}, 1, . . . \end{aligned}$
::b. 2,32,65,1,...

3. An ant colony invades the caramels in a candy store. The 1st day they eat $\begin{aligned} \frac{1}{4} \end{aligned}$ of a caramel, the 2nd day $\begin{aligned} \frac{1}{2} \end{aligned}$ of a caramel, and the 3rd day $\begin{aligned} \frac{3}{4} \end{aligned}$ . How many will they eat on the 4th, 5th, and 6th days?
::3. 蚂蚁聚居地侵入糖果店的焦糖,第一天他们吃14焦糖,第二天吃12焦糖,第三天吃34,第四、第五和第六天他们要吃多少?

4. Determine whether the sequence $\begin{aligned} 2^{2}, 3^{3}, 4^{4}, 5^{5}, 6^{6}, 7^{7}, \dots \end{aligned}$ is arithmetic.
::4. 确定22,33,44,55,66,77... 序列是否算术。

5. Do the sequences with formulas $\begin{aligned} a_{n} = 3 n - 1 \end{aligned}$ and $\begin{aligned} a_{n} = n + 7 \end{aligned}$ have a common term?
::5. 公式 an=3n-1 和 an=n+7 的序列是否有共同的术语?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try the following interactives to reinforce the concepts explored in this section:
::尝试以下互动来强化本节所探讨的概念:

References
::参考参考资料

1. "Halley's Comet," accessed May 12, 2017,
::2017年5月12日,

章节大纲

Arithmetic Sequences ::亚学序列

Example 1 ::例1

Example 2 ::例2

n th Term of Arithmetic Sequence ::nth 亚学序列期数

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

References ::参考参考资料

Arithmetic Sequences
::亚学序列

Example 1
::例1

Example 2
::例2

n ^th Term of Arithmetic Sequence
::nth 亚学序列期数

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Example 8
::例8

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX

References
::参考参考资料