答复 - Ch 11:指数和对数函数
章节大纲
-
Section 11.2 One-to-One Functions
::第11.2款.一对一职能Review
::回顾-
Not a function
::非函数函数 -
Function, but not one-to-one
::函数, 但不是一对一 -
Yes, a one-to-one function
::是, 一对一函数 - 12, 6, 18
- 20, 21, 110
-
A function, but
not one-to-one
::函数,但不是一对一 -
Yes, a one-to-one function
::是, 一对一函数 -
Yes, a one-to-one function
::是, 一对一函数 -
If
n
is even, it is not one-to-one, but is still a function.
::如果n为偶数,则不是一对一,但仍是一个函数。 -
Not a function of
x
::不是 x 函数的 x -
Not a function
::非函数函数 -
Function, but not one-to-one
::函数, 但不是一对一 -
Not a function
::非函数函数 -
Yes, a one-to-one function
::是, 一对一函数 -
Yes, a one-to-one function
::是, 一对一函数
Explore More
::探索更多-
If a graph passes the horizontal line test, the graph represents a one-to-one function.
::如果图形通过水平线测试,该图代表一对一的函数。 -
Answers will vary but could include, for example, any linear function in the form of
y
=
m
x
+
b
,
or any function that passes the horizontal line test.
::答案会有所不同,但可以包括,例如,y=mx+b形式的任何线性函数,或通过水平线测试的任何函数。 -
Answers will vary but could include, for example, any function in the form
y
=
x
n
,
where n is even. A function is not one-to-one if it fails the horizontal line test.
::答案会有所不同,但可以包括,例如,以y=xn形式出现的任何函数,n是偶数。如果一个函数不通过水平线测试,则该函数不是一对一。 -
A function is strictly increasing when, if
x
1
<
x
2
,
then
f
(
x
1
)
<
f
(
x
2
)
. All functions that are strictly increasing are one-to-one. A function is strictly decreasing if, when
x
1
<
x
2
, then
f
(
x
1
)
>
f
(
x
2
)
.
All functions that are strictly decreasing are one-to-one.
::如果 x1 < x2, 然后f(x1) < f(x2) , 函数将严格递增 。 如果, 当 x1 < x2, 然后f(x1) > f(x2) 所有严格递增的函数都是一对一时, 函数将严格递减 。 如果, 当 x1 < x2, 然后f(x1) > f(x2) 所有严格递减的函数都是一对一时, 函数将严格递减 。
Section 11.3 Inverse Functions
::第11.3节 反向职能Review
::回顾-
(
3
,
2
)
,
(
8
,
-
4
)
,
(
9
,
-
5
)
,
(
1
,
1
)
.
Yes, the inverse is a function.
:3,2,(8,4),(9,5),(1,1)。 是的,反之亦然。
-
(
-
6
,
9
)
,
(
-
5
,
8
)
,
(
3
,
7
)
,
(
3
,
4
)
.
No, the inverse is not a function.
:6,9,(5,8,),(3,7,),(3,4(4,4)。)不,反之,不是一种职能。
-
(
-
2
,
-
4
)
,
(
0
,
-
3
)
,
(
1
,
-
1
)
,
(
3
,
0
)
,
(
4
,
4
)
.
Yes, the inverse is a function.
:二)-4,(0)-3,(1)-1,(3)-0,(4)4,是的,反之亦然。
-
y
=
1
6
x
+
3
2
::y=16x+32 -
y
=
1
−
3
x
4
x
;
x
≠
0
::y= 1 - 3x4x; x% 0 -
y
=
x
2
−
7
::y=x2-7 y=x2-7 -
y
=
±
√
x
−
5
;
x
≥
5
::yx - 5; x=5 -
y
=
3
√
x
+
11
::y=3x+11 -
y
=
x
5
−
16
::y=x5 - 16 y=x5 - 16 -
y
=
7
x
−
1
;
x
≠
1
::y= 7x- 1; x% 1 -
y
=
8
x
x
−
1
;
x
≠
1
::y=8xx- 1;x% 1 -
Yes, since
f
(
g
(
x
)
)
=
x
.
::是,自f(g(x))=x -
No, since
f
(
g
(
x
)
)
≠
x
.
::否,自f(g(x))___x -
No, since
f
(
g
(
x
)
)
≠
x
.
::否,自f(g(x))___x -
Yes, since
f
(
g
(
x
)
)
=
x
.
::是,自f(g(x))=x
Explore More
::探索更多-
C
=
5
9
F
−
32
. If you substitute
F
=
9
5
C
+
32
into the equation
C
=
5
9
F
−
32
, you end up with
C
=
C
.
::C=59F-32. 如果在方程式C=59F-32中用 F=95C+32替代F=95C+32,最后用C=C。 -
No, they do not.
::不,他们没有。 -
r
≅
1.954
or
r
=
2
√
3
π
π
.
::r1.954或r=23。 -
d
=
p
3
2
.
::d=p32。 =p32。 =p32。 =p32。 -
Finding the inverse of
y
=
x
, you would switch
x
and
y
in the equation, which would give you the same equation.
::查找 y=x 的反方向, 您可以在方程中切换 x 和 y , 这样您就会得到相同的方程 。 -
If a function is a constant, such as
f
(
x
)
=
b
, then it does not have an inverse, but it will also fail the horizontal line test, so it is not actually a function.
::如果函数是一个常数,如f(x)=b,则该函数没有反函数,但也会失败水平线测试,因此它实际上不是一个函数。 -
Let
U
be the number of U.S. dollars, and
B
be the number of bitcoins. Then
U
=
B
×
1
U
0.00082
B
,
and the inverse would be
B
=
U
×
0.00082
B
1
U
,
and 1 bitcoin is worth $1,219.51.
::以美元计数, B 以比特币计数。 然后U=Bx1UN000082B, 反比特币为B=Ux0.00082BU, 1比特币值1 219.51美元。
Section 11.4 Exponential Functions
::第11.4节Review
::回顾-
a. No. b. No. c. No. d. Yes,
y
=
-
2
x
.
::a. b. b. c. d. 是,y=-2x. -
a. Growth. b. Growth. c. Decay. d. Growth. e. Decay
::a. 增长b. 增长c. 增长c. 下降 d. 增长e. 下降 -
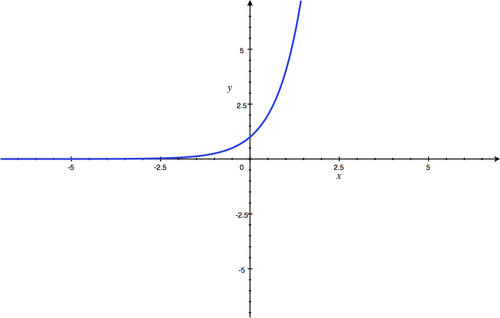
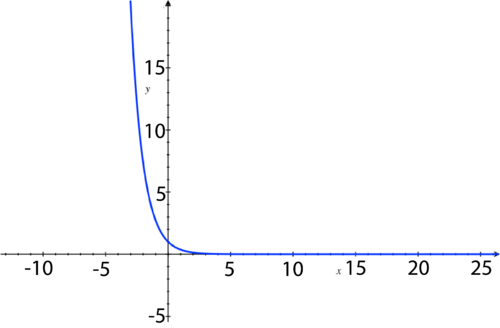
y
-intercept:
(
0
,
1
)
; Horizontal Asymptote:
y
=
0
; Domain: all real numbers; Range:
y
>
0
.
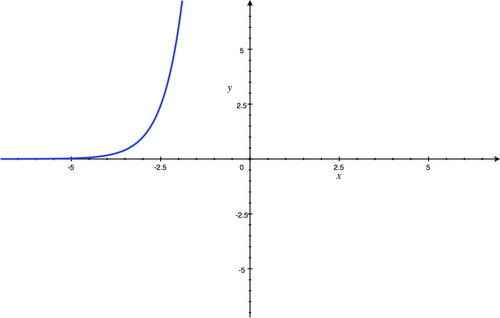
::y 拦截 : (0, 1) ; 水平单点 : y=0; 域 : 所有真实数字; 范围 : y>0 。 -
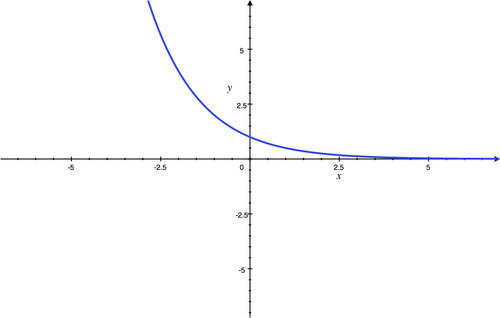
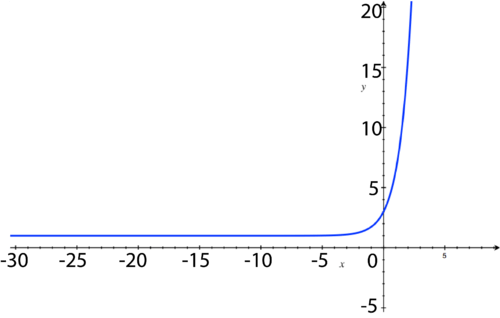
y
-intercept:
(
0
,
1
)
; Horizontal Asymptote:
y
=
0
; Domain: all real numbers; Range:
y
>
0
.
::y 拦截 : (0, 1) ; 水平单点 : y=0; 域 : 所有真实数字; 范围 : y>0 。 -
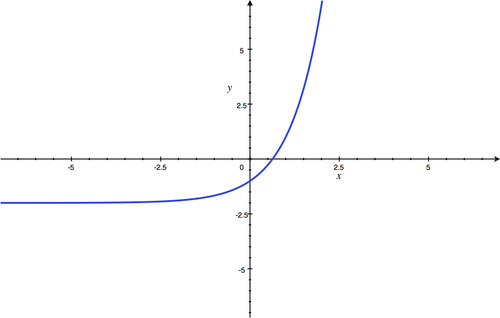
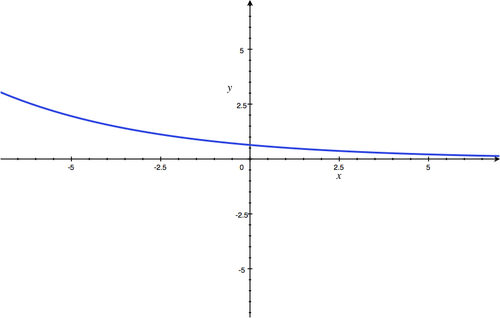
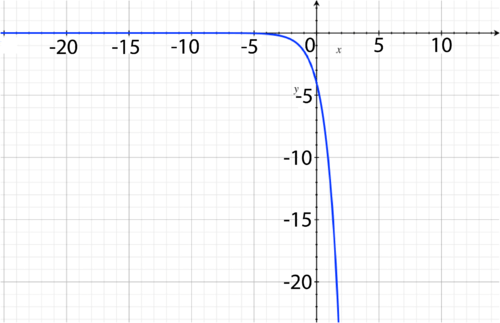
y
-intercept:
(
0
,
-
1
)
; Horizontal Asymptote:
y
=
0
; Domain: all real numbers; Range:
y
<
0
.
::y 截取 : (0, - 1); 水平渐渐淡化 : y=0; 域 : 所有真实数字 ; 范围 : y < 0 。 -
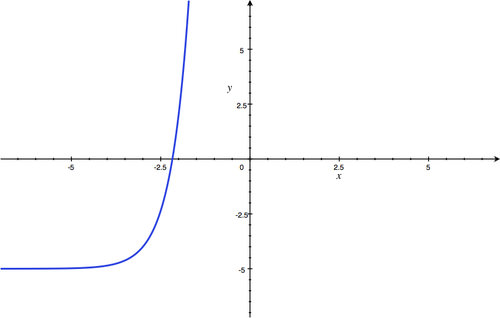
y
-intercept:
(
0
,
-
1
)
; Horizontal Asymptote:
y
=
-
2
; Domain: all real numbers; Range:
y
>
-
2
.
::y 拦截 : (0 , - 1 ); 水平单点 : y= 2; 域 : 所有实际数字; 范围 : y> 2 。 -
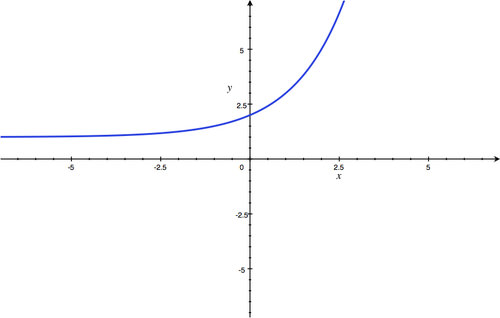
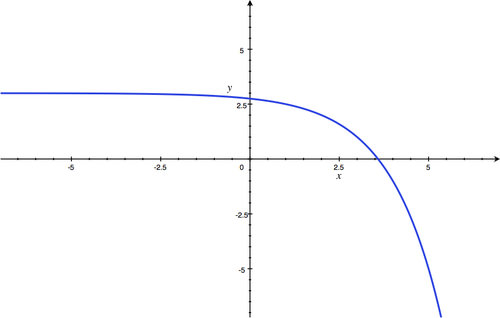
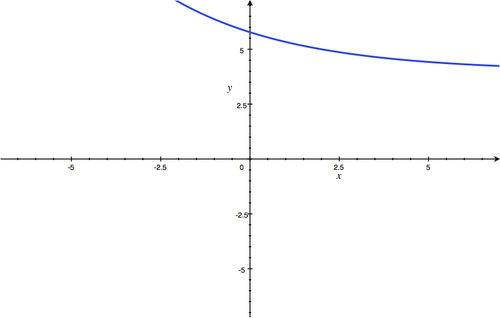
y
-intercept:
(
0
,
2
)
; Horizontal Asymptote:
y
=
1
; Domain: all real numbers; Range:
y
>
1
.
::y 拦截 : (0 , 2 ) ; 水平单点 : y= 1; 域 : 所有真实数字; 范围 : y > 1 。 -
y
-intercept:
(
0
,
216
)
; Horizontal Asymptote:
y
=
0
; Domain: all real numbers; Range:
y
>
0
.
::y 拦截0, 216 ) ; 水平定时 : y=0; 域 : 所有实际数字; 范围 : y>0 。
-
y
-intercept:
(
0
,
0.64
)
; Horizontal Asymptote:
y
=
0
; Domain: all real numbers; Range:
y
>
0
.
::y 拦截 : (0,0. 0. 64); 水平淡化 : y=0; 域 : 所有真实数字; 范围 : y>0 。 -
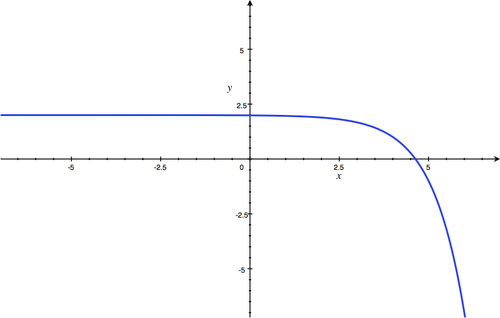
y-intercept:
(
0
,
2.75
)
; Horizontal Asymptote:
y
=
3
; Domain: all real numbers; Range:
y
<
3
.
::y 拦截 : (0, 2. 75); 水平淡化 : y= 3; 域 : 所有真实数字; 范围 : y < 3 。 -
y
-intercept:
(
0
,
338
)
; Horizontal Asymptote:
y
=
-
5
; Domain: all real numbers; Range:
y
>
-
5
.
::y 拦截0, 338 ) ; 水平单数 : y= 5; 域 : 所有实际数字; 范围 : y> 5 。
-
y
-intercept:
(
0
,
5.78
)
; Horizontal Asymptote:
y
=
4
; Domain: all real numbers; Range:
y
>
4
.
::y 界面 : (0, 5. 78); 水平单数 : y= 4; 域 : 所有真实数字; 范围 : y> 4 。 -
y
-intercept:
(
0
,
1.99
)
; Horizontal Asymptote:
y
=
2
; Domain: all real numbers; Range:
y
<
2
.
::y 拦截 : (0, 1. 99); 水平淡化 : y=2; 域 : 所有真实数字; 范围 : y < 2 。
Explore More
::探索更多-
a. 63 games. b. 67 games.
::a. 63场比赛. b. 67场比赛。 -
a. $16,288.95. b. $26,532.98.
::a. 16 288.95美元b. 26 532.98美元。 -
7,737 people
::7 737,373人 -
a.
y
=
50
(
0.90
)
x
.
b. $29.52. c. after about 6.5 weeks.
::ay=50(0.90)x.b.29.52.c.在大约6.5周之后。 -
1.845
×
10
19
grains of rice.
::1.845×1019谷物大米。 -
8.824978
2 3.14 8.8152409 2 3.141 8.8213533 2 3.1415 8.8244111 2 3.14159 8.8249616 2 3.141592 8.8249738 2 π 8.8249778
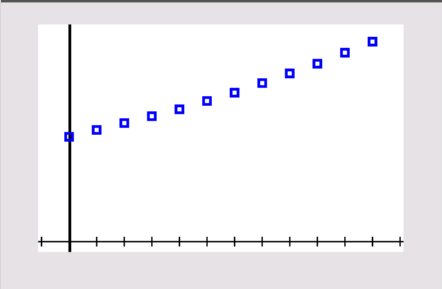
7. This graph represents an exponential function, since there is a common ratio of 1.06. The savings increase as the years increase. (Please note this sample graph is based on years since 2010.)
::7. 本图代表指数函数,因为共同比率为1.06,随着年数增加,节省额会增加。 (请注意,本样本图以2010年以来的年份为基础。 )Section 11.5 The Number e
::第11.5节 编号eReview
::回顾-
a. Growth since
x
is positive. b. Growth since there is a reflection in the
x
-axis. c. Decay since
x
is negative. d. Decay since
x
is negative.
::a. 由于x为正数而增长;b. 由于X轴反射为负数而增长;c. 由于x为负数而衰减;d. 由于x为负数而衰减;b. 由于x为负数而增长;c. 由于x为负数而衰减。 -
e
9
::e9 -
e
4
4
::e44 -
5
e
-
7
::5e-7 -
6
e
1
::6e1 -
9
16
e
6
::916e6 -
-
-
-
Explore More
::探索更多-
a. 173,325 people. b. Between 2024 and 2025, the population will double.
::a. 173 325人b. 在2024年至2025年期间,人口将翻一番。 -
a. $19,666. b. $7,530.
::a. 19 666美元,b. 7 530美元。 -
a.
A
=
7
,
500
e
0.045
t
.
b. $171. c. $10,750.
::a. A=7 500e0.045t. b. 171.c. 10 750美元。 -
6,000 g
::6 000克 6 000克 - $105.17
- 2.716666667
- 42.10
Section 11.6 Evaluating Logarithms
::第11.6节 评价对数Review
::回顾-
l
o
g
3
5
=
x
::log35=x -
l
o
g
a
b
=
x
::对数ab=x -
l
o
g
5
2.5
=
x
::log52.5=x -
2
x
=
32
::2x=32 -
(
1
3
)
-
2
=
x
:13)-2=x
-
a
b
=
y
::ab=y - 2
- -3
- -1
- 6
- 6
- 0
- 2.079
- 3.585
- 1.445
Explore More
::探索更多-
230.71 degrees
::230.71度 -
249.00 km/hr
::249.00公里/小时 -
1,150.51 N
::1 150.51 N -
Approximately 37.22 lbs
::约37.22磅
Section 11.7 Logarithmic Functions
::第11.7节 对数函数Review
::回顾-
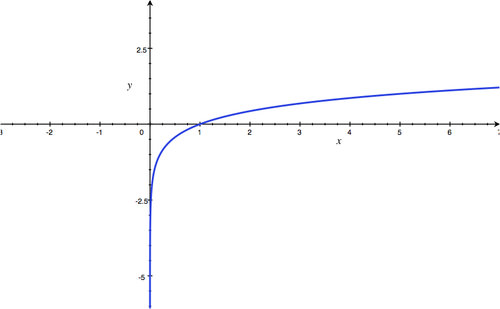
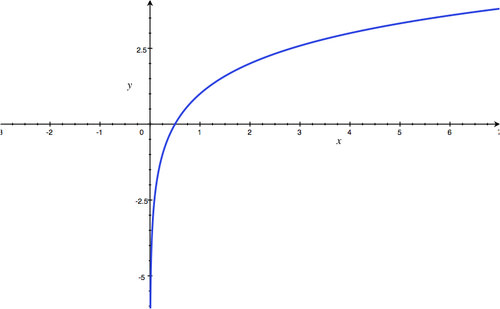
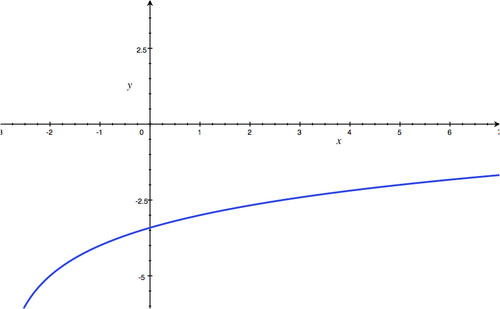
Asymptote:
x
=
0
; Domain:
(
0
,
∞
)
; Range:
(
-
∞
,
∞
)
.
::时点 : x=0; 域 : (0, ); 范围 : (- , ) 。 -
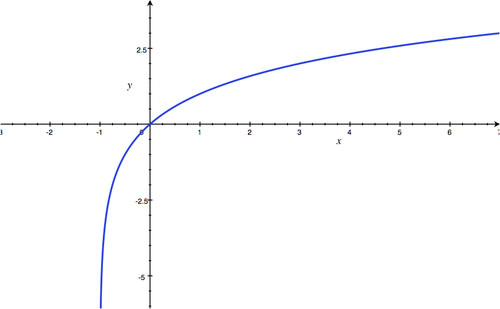
Asymptote:
x
=
0
; Domain:
(
0
,
∞
)
; Range:
(
-
∞
,
∞
)
.
::时点 : x=0; 域 : (0, ); 范围 : (- , ) 。 -
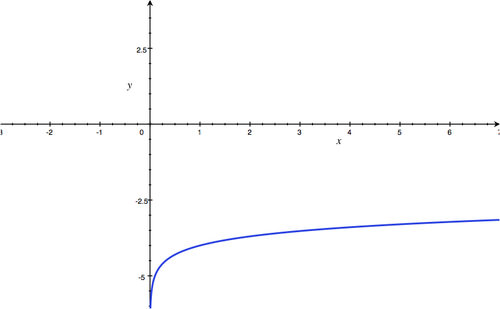
Asymptote:
x
=
-
1
; Domain:
(
-
1
,
∞
)
; R
ange:
(
-
∞
,
∞
)
.
::时点 : x=-1; 域 : (-1) ; 范围 : (-) , ) 。 -
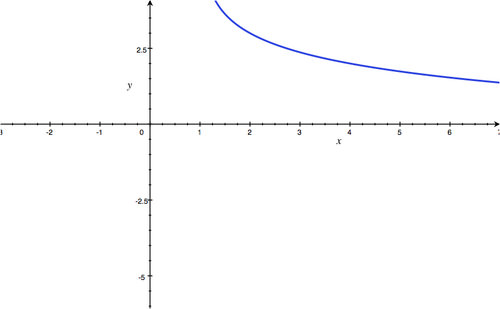
Asymptote:
x
=
0
; Domain:
(
0
,
∞
)
; R
ange:
(
-
∞
,
∞
)
.
::时点 : x=0; 域 : (0, ); 范围 : (- , ) 。 -
Asymptote:
x
=
1
; Domain:
(
1
,
∞
)
; R
ange:
(
-
∞
,
∞
)
.
::时间点 : x=1; 域 : (1, ); 范围 : (- , ) 。 -
Asymptote:
x
=
-
3
; Domain:
(
-
3
,
∞
)
; R
ange:
(
-
∞
,
∞
)
.
::时点 : x=-3; 域 : (3) ; 范围 : (-) , 。 -
Asymptote:
x
=
2
; Domain:
(
-
∞
,
2
)
; R
ange:
(
-
∞
,
∞
)
.
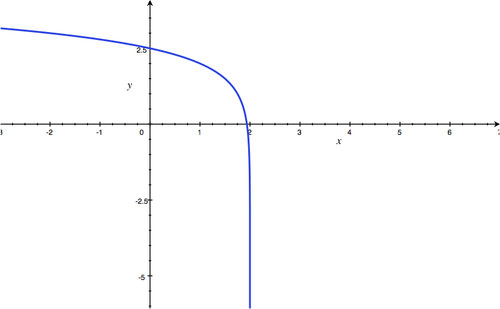
::时点 : x=2; 域 : (- , 2); 范围 : (- , ) 。 -
Yes
::是 是 -
No
::否 无 -
No
::否 无
Explore More
::探索更多-
-3.01 Db
::-3.01 Db -
301.03 km/s
::301.03公里/秒 -
10 times
::10 次 10 次 -
The graph would be horizontally translated
a
units to the right.
::图表将水平转换成向右的单位。 -
The graph would be reflected in the
x
-axis and have a stretch of
a
units.
::该图将反映在x轴中,并有一个单位的伸展。
Section 11.8 Logarithm Properties
::第11.8节对数属性Review
::回顾-
3
x
::3x 3进 -
-
x
::-xx -
x
+
3
::x+3 x+3 -
2
(
x
−
1
)
::2(x-1) -
x
−
7
::x-7 次-7 次 -
-
6
x
::-6x6x -
2
log
7
y
::2log7y 2log7y -
3
(
log
4
9
+
log
4
x
)
::3(log49+log4x) -
ln
(
5
)
or 1.609
:5) 或 1.609
-
log
11
2
or 0.2891
::log112 或 0.2891 -
log
12
5
+
2
log
12
z
::log125+2log12z -
log
6
5
+
log
6
x
::对数 65+log6x -
log
3
a
+
log
3
b
+
log
3
c
::对数 3a+log3b+log3c -
log
9
x
+
log
9
y
−
log
9
5
::log9x+log9y-log95 -
%7D">
log
(
2
)
+
log
(
x
)
−
log
(
y
)
::log(2)+log(x) -log -
log
4
5
−
(
log
4
9
+
log
4
y
)
::log45 - (log49+log4y) -
y
=
ln
(
x
3
)
−
2
::y=ln( x3)- 2 -
f
(
x
)
=
7
ln
(
5
x
)
:xx)=7ln(5x)
-
y
=
1
2
(
ln
(
x
−
2
)
+
3
)
::y=12( ln(x-2)+3) -
g
(
x
)
=
1
3
(
5
x
+
1
)
::g(x)=13(5x+1) -
y
=
-
2
⋅
10
x
::y=-210x -
y
=
e
x
+
2
4
::y=ex+24 y=ex+24
Explore More
::探索更多- 24
-
Answers will vary, but should include examples of the warnings about a log raised to a power, an exponent of a log moved in front of multiple logs, and incorrect uses of the quotient and product rules.
::答复会各有不同,但应包括警告的例子,警告的对象是电源的日志、在多个日志前移动的日志的标语、以及错误使用商数和产品规则。 -
Yes; you are just applying the power rule.
::是的,你只是在应用权力规则。 -
In the last step,
log
(
1
2
)
≠
1
2
and
log
(
1
8
)
≠
1
8
. In fact, there's an inverse relationship between the two values.
::在最后一步,对数( 12) \\\ 12 和对数( 18) \\\ 18。 事实上, 这两个值之间存在反向关系 。
Section 11.9 Simplifying and Expanding Logarithms
::第11.9节 简化和扩大对数Review
::回顾-
%5Cright)">
2
(
log
(
3
)
+
log
(
x
)
−
log
(
y
)
)
::2(log(3)+log(x)-log))
-
%7D-4%7B%5Clog%7D_%7B8%7D%7B(z)%7D">
3
log
8
(
x
)
+
2
log
8
(
y
)
−
4
log
8
(
z
)
::3log8(x)+2log8-4log8(z)
-
%7D%5Cright)">
2
(
2
+
4
log
5
(
x
)
−
log
5
(
y
)
)
::2(2+4log5(x)-)
-
%5Cright)">
-
2
(
ln
(
6
)
+
ln
(
x
)
−
3
ln
(
y
)
)
:2)(6)+ln(xx)-3ln
-
%5Cright)">
6
(
5
−
2
ln
(
x
)
−
3
ln
(
y
)
)
::6(5--2ln(x)-3ln)
-
log
6
(
x
2
y
5
)
::对数 6(x2y5) -
log
3
(
6
y
4
)
or
log
3
(
3
y
2
)
::log3( 6y4) 或log3( 3y2) -
log
(
12
y
2
x
)
::日志( 12y2x) -
log
6
(
x
y
)
::对数 6(xy) -
log
(
x
y
)
3
::log(xy)3 对数 -
log
(
√
x
+
1
y
3
)
::日志(x+1y3) -
log
2
(
y
4
x
)
::log2(y4x) -
log
2
(
5
(
x
−
3
)
10
y
)
1
5
::log2( 5( x- 3) 10y) 15 -
(
l
o
g
3
(
√
y
3
√
x
⋅
z
)
)
4
:log3(y3xz))4
Section 11.10 Solving Exponential Equations
::第11.10节 解决指数等价物Review
::回顾- 2.594
- 2.219
- 6.492
- 5.424
- 0.285
- 1.165
- 3.142
- 4.869
- 1.5
- 3.5
- 1
- 3
- 6
- 3
- 2
Explore More
::探索更多- $1,293.83
- $39,419.18
Section 11.11 Solving Logarithmic Equations
::第11.11节 解决对数等数Review
::回顾- 32,768
- 498.831
- 86
- 170
- 1.132
- 1.442
-
2 is a solution, and -7 is extraneous.
::2是解决办法,7是无关紧要的。 -
No solution
::无解决方案 - 8
- 27
- 2
- 3.272
-
4
3
is a solution, and
-
1
2
is extraneous.
::43是一个解决方案, 而 -12是无关紧要的。 -
8.633 is a solution, and -4.633 is extraneous.
::8.633是一种解决办法,而-4.633是无关紧要的。 - 6
Explore More
::探索更多- 3.16 × 10 - 6
- 0.316
-
a. 251.2. b. 1,584.9
::a. 251.2.b. 1 584.9
Section 11.12 Exponential Growth and Decay Models
::第11.12节 指数增长和衰减模型Review
::回顾- $61,600
- $8,089
-
Yes
::是 是 - $ 31,200
- $ 143,000
- $377,000
-
168,156 people
::168 156人 -
15 years
::15岁 -
0.195 grams
::0.195克 -
747 rabbits
::747只兔子 -
a.
A
=
A
0
e
-
0.433217
t
. b. 1.719383 grams. c. 6.815673 grams.
::a. A=A0e-0.433217t. b. 1.719383克. c. 6.81673克。 - 0.076017
- $35,476
Section 11.13 Compound Interest
::第11.13款 复合利息Review
::回顾- $17,890
- $10,759
- $40,870
- $16,405
- $18,529
- $7,800
- 7%
- $3,831.14
-
No, the interest rate is higher at his current bank (5.99%).
::不,他的现期银行利率较高(5.99%)。 - $6,127.38
Section 11.14 Connections: How Many People Are Too Many?
::第11.14节:关联:有多少人太多?-
y
=
2.24
×
10
-
8
(
1.0167
)
x
::y=2.24×10-8(1.0167x) -
y
=
1.20
×
10
-
4
(
1.0124
)
x
::y=1. 20x10-4(1.0124)x -
Model 1: 28.5 billion. Model 2: 20.8 billion
::模式1:285亿,模式2:208亿 -
::答案将有所不同,但1950年至2012年的预测模型为y=1.231x10-8(1.017x),2100年人口为320亿。 -
::2.09×107英尺 -
::5.49×1015ft2 -
::7.08×1014ft2 -
::7.08×1012ft2 -
::模型1:2850 模型2:3133。
Section 11.15 Connections: Are You an Acid or a Base?
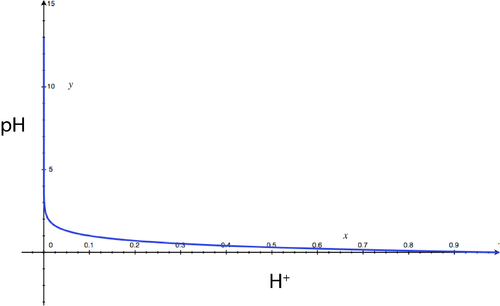
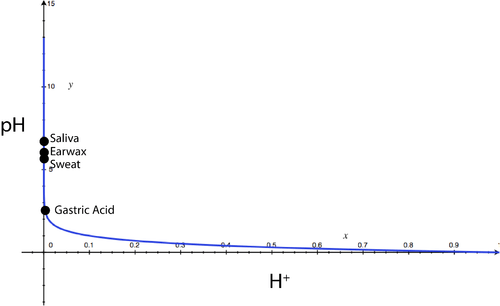
::第11.15节连接:你是酸类还是碱类?-
-
-
[
H
+
]
=
2.51
×
10
-
8
when the pH is 7.6, and
[
H
+
]
=
3.55
×
10
-
8
when the pH is 7.45.
::[H+]=2.51×10-8,pH值为7.6,[H+]=3.55×10-8,pH值为7.45。 -
[
H
+
]
=
7.94
×
10
-
8
when the pH is 7.1, and
[
H
+
]
=
4.47
×
10
−
8
when the pH is 7.35.
::[H+]=7.94×10-8,pH值为7.1;和[H+]=4.47×10-8,pH值为7.35。
-
Not a function